Teopeмa сложения скоростей

Пусть некоторая точка М со­вершает движение по отношению к системе отсчета Oxyz, которая са­ма движется произвольным образом по отношению к неподвижной систе­ме отсчета 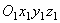, (рис.49).

Конечно, абсолютное движение точки М определяется уравнениями

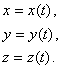
Относительное движение – в движущихся осях уравнениями

Рис. 10.3.

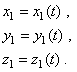
Уравнений, определяющих переносное движение точки, не может быть вообще. Так как, по определению, переносное движение точки М – это движение относительно неподвижных осей той точки системы 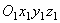, с которой совпадает точка в данный момент. Но все точки подвижной сис­темы движутся по-разному.

Поло­жение подвижной системы отсчета может быть также определено, если задать положение точки О радиусом-вектором 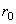, проведенным из начала неподвижной системы отсчета, и направления единичных векторов 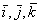подвижных осей Оx, Oy, Oz.

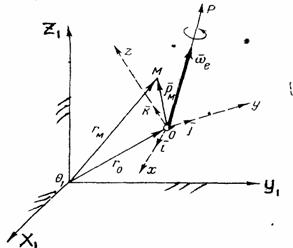
Рис.49

Произвольное переносное движение подвижной системы отсчета слагается из поступательного движения со скоростью 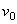точки О и движения вокруг мгновенной оси вращения ОР, походящей через точку О, с мгновенной угловой скоростью 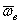. Вследствие переносного движения подвижной системы отсчета радиус-вектора 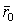и направления единичных векторов 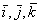изменяются. Если векторы 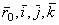заданы в функции времени, то переносное движение подвижной системы отсчета вполне определено.

Положение точки М по отношению к подвижной системе отсчета можно определить радиусом-вектором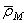

,

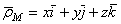где координаты x, y, z точки М изменяются с течением времени вследствие движения точки М относительно подвижной системы отсчета. Если радиус-вектор 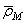задан в функции времени, то относительное движение точки М, т.е. движение этой точки относительно подвижной системы отсчета, задано.

Положение точки М относительно неподвижной системы отсчета 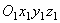, может быть определено радиусом-вектором 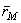. Из рис.49 видно, что

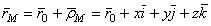. (1)

Если относительные координаты x,y,z точки М и векторы 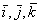определены в функции времени, то слагающееся из относительного и переносного движений составное движение точки М, т.е. движение этой точки по отношению к неподвижной системе отсчета, также надо считать заданным.

Скорость составного движения точки М, или абсолютная скорость этой точки, равна, очевидно, производной от радиуса-вектора 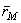точки M по времени t

.

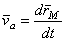Поэтому, дифференцируя равенство (1) по времени t, получим

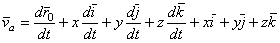. (2)

Разобьем слагаемые в правой части этого равенства на две группы по следующему признаку. К первой группе отнесем те слагаемые, которые содержат производные только от относительных координат x,y,z, а ко второй - те слагаемые, которые содержат производные от векторов 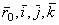, т.е. от величин, изменяющихся только вследствие переносного движения подвижной системы отсчета

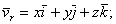(3)

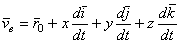. (4)

Каждая из групп слагаемых, обозначенных через 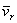и 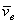, представляет собой, по крайней мере, по размерности некоторую скорость. Выясним физический смысл скоросте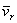й и _.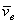

Скорость 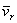, как это следует из равенства (3), вычисляется в предположении, что изменяются только относительные координаты x,y,z точки М, но векторы 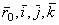остаются постоянными, т.е. подвижная система отсчета Oxyz как бы условно считается неподвижной. Итак, скорость 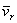представляет собой относительную скорость точки М.

Скорость 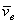вычисляется так, как будто бы точка М не двигалась относительно подвижной системы отсчета, так как производные x,y,z в равенство (4) не входят. Поэтому скорость 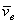представляет собой переносную скорость точки М.

Итак, 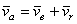. (5)

Это равенство выражает теорему сложения скоростей в случае, когда переносное движение является произвольным: абсолютная скорость точки М равна геометрической сумме переносной и относительной скоростей этой точки.

Теорема сложения ускорений. Ускорение Кориолиса.

Ускорение составного движения точки М, или абсолютное ускорение этой точки, равно, очевидно, производной от абсолютной скорости точки М по времени t

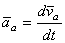
Поэтому, дифференцируя равенство по времени, получим

.

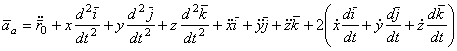Разделим слагаемые правой части этого равенства на три группы.

К первой группе отнесем слагаемые, содержащие только производные от относительных координат x,y и z, но не содержащие производные от векторов :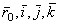

.

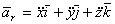Ко второй группе отнесем слагаемые, которые содержат только производные от векторов 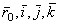, но не содержащие производных от относительных координат x,y,z:

.

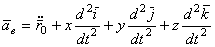Осталась еще одна группа слагаемых, которые не могли быть отнесены ни к первой, ни ко второй, так как они содержат производные от всех переменных x, y, z, 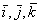. Обозначим эту группу слагаемых через :

.

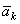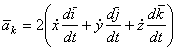Каждая из выделенных групп представляет собой, по крайней мере по размерности, некоторое ускорение. Выясним физический смысл всех трех ускорений: .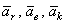

Ускорение 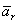, как это видно из равенства, вычисляется так, как если бы относительные координаты x,y,z изменялись с течением времени, а векторы 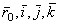оставались неизменными, т.е. подвижная система отсчета Oxyz как бы покоилась, а точка М двигалась. Поэтому ускорение 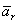представляет собой относительное ускорение точки М. Так как ускорение (и скорость) относительного движения вычисляется в предположении, что подвижная система отсчета находится а покое, то для определения относительного ускорения (и скорости) можно пользоваться всеми правилами, изложенными ранее в кинематике точки.

Ускорение 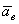, как это видно из равенства, вычисляется в предположении, что сама точка М покоится по отношению к подвижной системе отсчета Oxyz (x =const, y =const, z =const) и перемещается вместе с этой системой отсчета по отношению к неподвижной системе отсчета 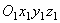. Поэтому ускорение 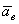представляет собой переносное ускорение точки М.

Третья группа слагаемых определяет ускорение 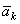, которое не может быть отнесено не к относительному ускорению 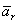, так как содержит в своем выражении производные 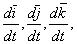не к переносному ускорению 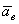, так как содержит в своем выражении производные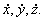

Преобразуем правую часть равенства, припомнив, что

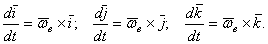
Подставляя эти значения производных в равенства, получим

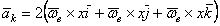
или .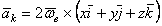

Здесь вектор 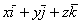есть относительная скорость 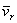точки М, поэтому

.

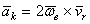Ускорение 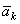называют ускорением Кориолиса. Ввиду того, что ускорение Кориолиса появляется в случае вращения подвижной системы отсчета, его называют еще поворотным ускорением.

С физической точки зрения появление поворотного ускорения точки объясняется взаимным влиянием переносного и относительного движений.

Итак, ускорение Кориолиса точки равно по модулю и направлению удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки.

Равенство, которое теперь можно сокращенно записать в виде

.

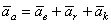представляет теорему сложения ускорений в случае, когда переносное движение является произвольным: абсолютное ускорение точки равно векторной сумме переносного, относительного и поворотного ускоре­ний. Эту теорему часто называют теоремой Кориолиса.

Из формулы следует, что модуль поворотного ускорения будет

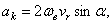
где 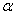- угол между вектором 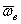и вектором 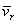. Чтобы определить направление поворотного ускорения 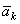, нужно мысленно перенести вектор 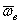в точку М и руководствоваться правилом векторной алгебры. Согласно этому правилу, вектор 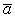нужно направлять перпендикуляр­но к плоскости, определяемой векторам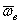и и 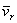, и так, чтобы, смотря с конца вектора 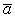, наблюдатель мог видеть кратчайший поворот от 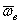к 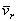происходящим против движения часовой стрелки (рис. 30).

Для определения направления 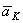можно также пользоваться следующим правилом Н. Е. Жу­ковского: чтобы получить направление поворот­ного ускорения 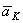, достаточно составляющую 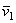относительной скорости 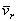точки М, перпенди­кулярную к вектору 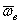, повернуть (в плоскости, перпендикулярной к вектору 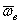) на прямой угол вокруг точки М в направлении переносного вра­щения (рис.51).

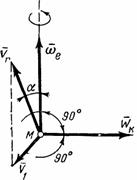
Рис.51

Если переносное движение подвижной систе­мы отсчета есть поступательное движение, то 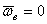и поэтому поворотное ускорение 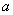точки также равно нулю. Поворотное ускорение равно, очевидно, нулю и в том случае, когда 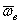в данный момент времени обращается в нуль.

Кроме того, поворотное ускорение точки может, очевидно, обращать­ся в нуль, если:

а) вектор относительной скорости 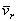точки параллелен вектору уг­ловой скорости 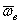переносного вращения, т.е. относительное движение точки происходит по направлению, параллельному оси переносного вращения;

б) точка не имеет движения относительно подвижной системы от­счета или относительная скорость 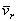точки в данный момент времени равна нулю ().

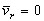23.Основные понятия и аксиомы динамики.Дифференциальные уравнения движения точки в инерциальной системе отсчета и две основные задачи динамики(прямая и обратная).
Аксиомы классической механики

Первая аксиома или закон инерции. Материальная точка, на которую не действуют силы или действует равновесная система сил, обладает способностью сохранять свое состояние покоя или равномерного и прямолинейного движения относительно инерциальной системы отсчета.

Материальная точка, на которую действует равновесная система сил, называется изолированной материальной точкой.

Равномерное и прямолинейное движение точки называется движением по инерции.

Вторая аксиома или основной закон динамики. Ускорение материальной точки относительно инерционной системы отсчета пропорционально приложенной к точке силе и направлено по этой силе.

m

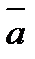
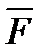
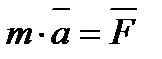
Положительный коэффициент пропорциональности m, характеризует инертные свойства материальной точки и называется массой точки.

Рис. 1-1

Масса не зависит от характеристик движения точки и от природы сил. Масса считается постоянной величиной и зависит только от самой материальной точки.

Сила, приложенная к материальной точке, всегда имеет материальный источник в виде других материальных тел, которые действуют на точку путем контакта при непосредственном соприкосновении с ней или на расстоянии через посредство силовых полей.

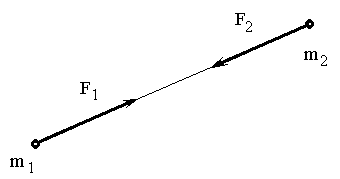Третья аксиома или закон о равенстве сил действия и противодействия. Силы взаимодействия двух материальных точек равны по величине и противоположны по направлению.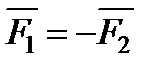

Рис. 1-2

Четвертая аксиома или закон независимого действия сил. При одновременном действии на материальную точку нескольких сил ускорение точки относительно инерционной системы отсчета от действия каждой отдельной силы не зависит от наличия других, приложенных к точке, сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.

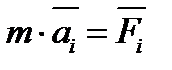
Дата добавления: 2015-06-04