Основные задачи динамики

Дифференциальные уравнения движения точки.

Основное уравнение динамики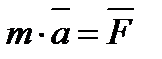

можно записать так 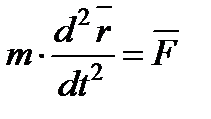или так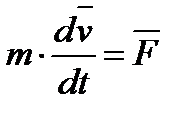

Проецируя уравнение 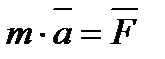на оси координат получаем

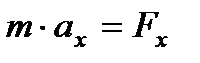
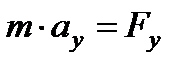
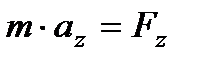
так как 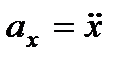, , 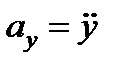, то

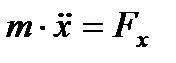
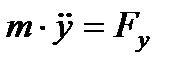
Частные случаи:

А) Точка движется в плоскости. Выбираем в плоскости координаты xOy получаем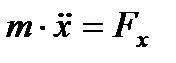

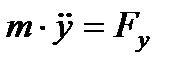
Б) Точка движется по прямой. Выбираем на прямой координату Ox получаем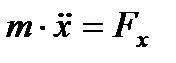

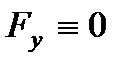
Основное уравнение динамики можно спроецировать на естественные подвижные оси.

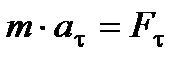
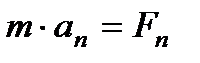
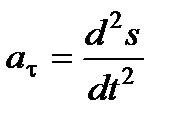
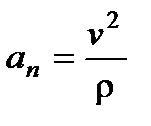
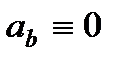
Эта форма уравнений удобна для исследования некоторых случаев полета снарядов и ракет.

Первая или прямая задача:

Известна масса точки и закон ее движения, необходимо найти действующую на точку силу.

m

Вычисляем вторые производные по времени от координат точки, умножаем их на массу и получаем проекции силы на оси координат

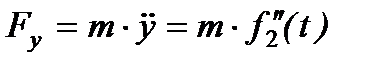
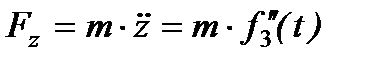
Зная проекции силы на оси координат, определяем модуль силы и ее направляющие косинусы:

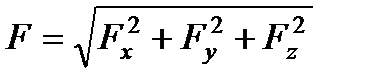
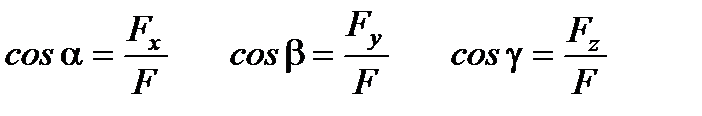
Вторая или обратная задача:

Известна масса точки и действующая на точку сила, необходимо определить закон движение этой точки.

Рассмотрим решение этой задачи в декартовой системе координат. Сила зависит от времени, координат точки, ее скорости и других причин.

, ,

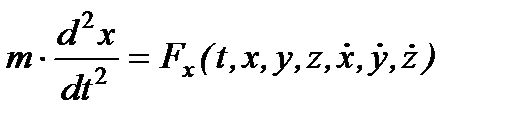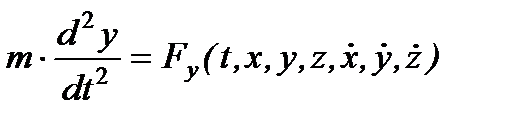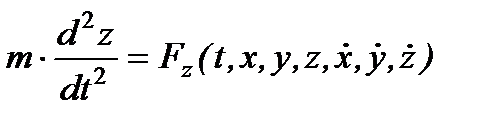
Из теории обыкновенных дифференциальных уравнений известно, что решение одного дифференциального уравнения второго порядка содержит две произвольные постоянные. Для случая системы трех обыкновенных дифференциальных уравнений второго порядка имеется шесть произвольных постоянных: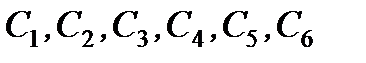

Каждая из координат 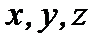движущейся точки после интегрирования системы уравнений зависит от времени и всех шести произвольных постоянных, т.е.

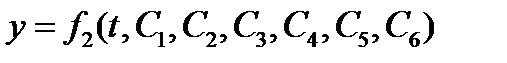
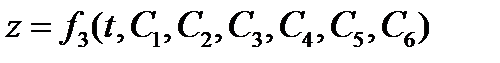
К этим уравнениям необходимо добавить начальные условия:

,

,

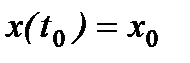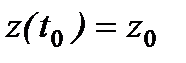
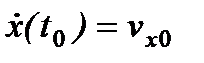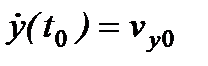
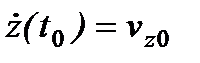
Используя эти начальные условия можно получить шесть алгебраических уравнений для определения шести произвольных постоянных 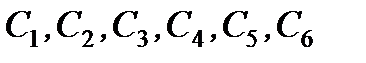. 24.Дифференциальные уравнения движения точки в неинерциальной системе отсчета.Переносная икориолисова силы инерции.Принцип относительности классической механики.

Для получения дифференциальных уравнений движения материальной точки в не 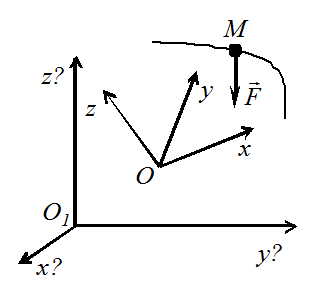инерциальной системе отсчета воспользуемся теоремой сложного движения точки, рассматривая ее движение одновременно в двух системах координат – основной (инерциальная система отсчета) и подвижной . Пусть 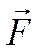- равнодействующая сил, действующих на точку 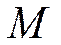(рис. 12.3). В инерциальной системе отсчета: .

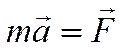Воспользуемся выражением для абсолютного ускорения точки (теорема Кориолиса):

.

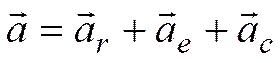Тогда ,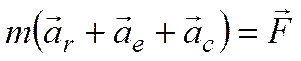

или .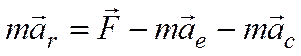

Величины 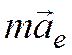и 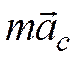имеют размерность силы. Вводя обозначения:

- переносная сила инерции,

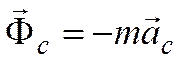- кориолисова сила инерции,

получаем основное уравнение динамики относительного движения

.

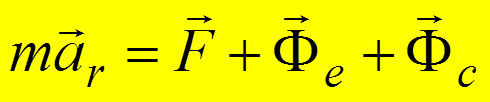Уравнение движения в подвижной системе координат не совпадает с основным уравнением динамики, следовательно, соответствующая система отсчета не является инерциальной.

Дата добавления: 2015-06-04