Вопросы по динамике

- Аналитическое задание связи, классификация связей.

- В чем состоит физический смысл диссипативной функции. Запишите соответствующую формулу.

- Влияние сил сопротивления на движение механических систем. Обобщенные силы, отвечающие силам вязкого трения. Функция Релея.

- Возможные и действительные перемещения.

- Вывести дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.

- Вывести дифференциальное уравнение вынужденных колебаний механической системы с одной степенью свободы без учета сопротивления. Изложить его решение в случае отсутствия резонанса.

- Вывести дифференциальное уравнение вынужденных колебаний механической системы с одной степенью свободы без учета сопротивления. Изложить его решение в случае резонанса. Графики амплитуды и сдвига фаз вынужденных колебаний.

- Вывести дифференциальное уравнение свободных движений механической системы с одной степенью свободы с учетом сил сопротивления. Изложить его решение в случае малого сопротивления.

- Вывести дифференциальное уравнение свободных движений механической системы с одной степенью свободы с учетом сил сопротивления. Изложить его решение в случаях критического и большего сопротивления.

- Вывести дифференциальное уравнение свободных колебаний механической системы с одной степенью свободы. Изложить его решение. Дать определение изохронизма свободных колебаний.

- Вывести закон движения материальной точки, брошенной под углом к горизонту.

- Вывести формулу главного момента количеств движения твердого тела относительно оси вращения.

- Вывести формулы главного вектора и главного момента сил инерции

- Вывести формулы работы силы, приложенной к твердому телу при различных случаях его движения.

- Вычислить главный вектор и главный момент сил инерции механической системы.

- Вычислить кинетическую энергию при плоскопараллельном движении твёрдого тела.

- Вычислить кинетическую энергию при поступательном и вращательном движениях твёрдого тела.

- Вычислить работу вращающего момента.

- Вычислить работу силы тяжести.

- Вычислить работу упругой силы.

- Геометрия масс. Свойства моментов инерции и их вычисление для однородного стержня.

- Гироскопические явления. Теорема Резаля. Действие кратковременной силы на гироскоп.

- Дайте определение действительного и возможного перемещения точки. Каковы их обозначения?

- Дайте определение и запишите формулу возможной работы силы. Какие связи называются идеальными?

- Дайте определение и запишите формулу момента количества движения материальной точки?

- Дайте определение и запишите формулы возможной работы силы. Сформулируйте определение идеальной связи.

- Дайте определение и запишите формулы главного момента количеств движения системы относительно точки и относительно оси.

- Дайте определение коэффициента восстановления. По какой формуле можно определить этот коэффициент опытным путем.

- Дайте определения массы, момента инерции, импульса силы, работы силы, количества движения, кинетической энергии.

- Дайте определение механической системы. Центр масс системы. Классификация сил действующих на систему. Запишите дифференциальные уравнения движения системы.

- Дайте определение обобщенных координат механической системы. Каковы их обозначения?

- Дайте определение силы инерции материальной точки. Запишите формулы касательной и нормальной сил инерции точки.

- Дать определение и указать способ вычисления количества движения механической системы.

- Дать определение кинетической энергии материальной точки и механической системы.

- Дать определение кинетической энергии точки и механической системы. Сформулировать и доказать теорему Кенига.

- Дать определение количества движения точки и механической системы. Доказать формулу для вычисления количества движения механической системы. Что такое элементарный и полный импульс силы.

- Дать определение момента количества движения материальной точки и механической системы относительно центра.

- Дать определение момента количества движения точки и главного момента количеств движения механической системы.

- Дать определение поверхности уровня потенциального силового поля и доказать их свойства.

- Дать определение потенциального силового поля. Доказать свойства стационарного потенциального силового поля.

- Дать определение потенциального силового поля. Указать способ вычисления работы потенциальных сил.

- Дать определение силовой функции и потенциальной энергии системы. Доказать закон сохранения полной механической энергии.

- Дать определение силы инерции точки. Сформулировать и обосновать принцип Даламбера для материальной точки.

- Дать определение центра масс механической системы.

- Дать определение явления удара. Изложить основные понятия и допущения элементарной теории удара

- Дать определения возможных скоростей и возможных перемещений материальной точки и механической системы.

- Дать определения материальной точки, механической системы, геометрически неизменяемой механической системы и абсолютно твёрдого тела.

- Дать определения мощности силы, элементарной работы силы и работы силы на конечном перемещении.

- Движение тела переменного состава. Уравнение Мещерского. Формула Циолковского.

- Динамика точки в неинерциальной системе координат. Случай равновесия.

- Динамические реакции в подшипниках твердого тела, вращающегося вокруг неподвижной оси.

- Дифференциальные уравнения вращения твердого тела вокруг неподвижной оси.

- Дифференциальные уравнения движения системы материальных точек.

- Дифференциальные уравнения Эйлера твердого тела с одной неподвижной точкой.

- Докажите условия равновесия механической системы в обобщенных координатах.

- Доказать вторую теорему Кёнига.

- Доказать и сформулировать законы сохранения движения центра масс.

- Доказать и сформулировать законы сохранения количества движения механической системы.

- Доказать необходимое и достаточное условия прямолинейного движения материальной точки и записать дифференциальное уравнение её прямолинейного движения.

- Доказать первую теорему Кёнига, устанавливающую связь между кинетическими моментами механической системы относительно её центра масс и любого неподвижного центра.

- Доказать приближенную формулу кинетической энергия системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия.

- Доказать приближенную формулу потенциальной энергия системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия.

- Доказать принцип возможных перемещений.

- Доказать теорему о движении центра масс механической системы.

- Доказать теорему о зависимости между моментами инерции относительно параллельных осей (теорему Гюйгенса–Штейнера).

- Доказать теорему об изменении кинетического момента механической системы относительно её центра масс.

- Доказать теорему об изменении кинетической энергии механической системы.

- Доказать теорему об изменении количества движения механической системы.

- Доказать теорему об изменении момента количества движения (кинетического момента) механической системы относительно неподвижного центра (неподвижной оси).

- Доказать формулы вычисления моментов инерции круга и однородного круглого цилиндра.

- Доказать формулы для вычисления кинетической энергии твердого тела в различных случаях его движения.

- Доказать формулы для вычисления моментов инерции прямолинейного тонкого стержня и прямоугольной пластины.

- Доказать чему равна работа внутренних сил, приложенных к твердому телу.

- Доказать, что суммарная мощность всех внутренних сил геометрически неизменяемой механической системы равна нулю.

- Зависимость веса тела от широты места.

- Законы Ньютона и две основные задачи динамики материальной точки.

- Записать дифференциальные уравнения движения материальной точки в проекциях на декартовы оси и на оси естественного трёхгранника.

- Записать дифференциальные уравнения движения точек механической системы. Дать определение внешних и внутренних сил.

- Записать уравнения Лагранжа 2-го рода. Привести пример составления этих уравнений.

- Запишите дифференциальное уравнение вращательного движения твердого тела.

- Запишите дифференциальное уравнение вынужденных колебаний системы с одной степенью свободы без учета сопротивления.

- Запишите дифференциальное уравнение малых движений системы с одной степенью свободы с учетом сил сопротивления.

- Запишите дифференциальное уравнение малых колебаний системы с одной степенью свободы.

- Запишите и сформулируйте теорему об изменении кинетической энергии точки в различных формах.

- Запишите приближенную формулу для диссипативной функции механической системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия.

- Запишите различные формулы для определения элементарной работы силы.

- Запишите уравнения Лагранжа II рода. Изложите последовательность действий при решении задач аналитической динамики с помощью уравнений Лагранжа II рода.

- Запишите уравнения Лагранжа II рода. Сколько этих уравнений можно составить для конкретной механической системы.

- Запишите формулу и сформулируйте теорему о движении центра масс.

- Запишите формулу и сформулируйте теорему о количестве движения материальной точки в дифференциальной форме?

- Запишите формулу и сформулируйте теорему об изменении количества движения материальной точки на конечном промежутке времени?

- Запишите формулу и сформулируйте теорему об изменении количества движения системы в интегральной форме в векторном виде.

- Запишите формулу и сформулируйте, чему равен главный вектора сил инерции механической системы.

- Запишите формулу и сформулируйте, чему равен главный момент сил инерции механической системы.

- Запишите формулы для кинетической и потенциальной энергии механической системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия.

- Запишите формулы для нахождения положения центра масс материальной системы.

- Идеальные связи. Проблема замыкания уравнений Ньютона для систем со связями.

- Изложите вывод принципа Даламбера–Лагранжа (общего уравнения динамики), сформулируйте его и запишите соответствующие формулы в векторной и аналитической формах.

- Изложите вывод уравнений Лагранжа II рода в случае потенциального поля сил. Что такое функция Лагранжа.

- Изложить последовательность интегрирования дифференциального уравнения прямолинейного движения точки в случае, когда сила зависит только от времени.

- Изложить последовательность интегрирования дифференциального уравнения прямолинейного движения точки в случае, когда сила зависит только от скорости.

- Изложить последовательность интегрирования дифференциального уравнения прямолинейного движения точки в случае, когда сила зависит только от координаты точки.

- Как в аналитической динамике вводится понятие обобщенные силы. Изложите способы вычисления обобщенных сил.

- Как вычисляется работа потенциальных сил на конечном перемещении точки?

- Как вычисляется элементарная и полная работа переменной по величине и направлению силы на криволинейном участке траектории?

- Как вычисляются силовые функции однородного поля силы тяжести и линейной силы упругости.

- Как записывается и формулируется теорема об изменении момента количества движения материальной точки?

- Как определить кинетическую энергию системы, состоящей из нескольких тел?

- Как определяется работа однородных сил тяжести, действующих на систему?

- Как формулируются условия равновесия механической системы в обобщенных координатах.

- Какое уравнение называется дифференциальным уравнением динамики? Какой алгоритм решения задач динамики с помощью дифференциальных уравнений?

- Какие оси называются осями Кёнига? Запишите и сформулируйте теорему Кёнига.

- Какие силы называются потенциальными? Приведите примеры потенциальных сил.

- Какой вывод можно сделать о движении центра масс, если главный вектор внешних сил системы равен нулю?

- Кинематические уравнения Эйлера.

- Кинетическая энергия твердого тела в общем случае движения.

- Кинетическая энергия твердого тела при поступательном, вращательном и плоском движениях.

- Кинетическая энергия твердого тела с одной неподвижной точкой.

- Кинетическая энергия. Теорема Кенига.

- Кинетический момент и его проекции на оси координат. Связь между моментами количества движения относительно разных точек.

- Кинетический момент относительно центра масс в абсолютном и относительном движении.

- Кинетический момент твердого тела относительно неподвижной оси.

- Кинетический момент твердого тела относительно неподвижной точки.

- Линейное сопротивление и диссипативная функция. Доказать приближенную формулу диссипативной функции системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия.

- Механический смысл функции Релея.

- Момент инерции относительно произвольной оси, проходящей через данную точку.

- Напишите дифференциальные уравнения движения несвободной точки в проекциях на оси декартовой системы координат.

- Напишите дифференциальные уравнения движения свободной точки в проекциях на оси декартовой системы координат.

- Напишите дифференциальные уравнения движения свободной точки в проекциях на естественные оси координат.

- Напишите и сформулируйте теорему об изменении количества движения системы в дифференциальной форме в векторном виде.

- Напишите формулы для определения кинетической энергии тела, совершающего: поступательное, вращательное, плоское движения.

- Напишите формулы для определения моментов количеств движения системы относительно осей декартовой системы координат.

- Напишите формулы для определения элементарной работы силы, приложенной к вращающемуся телу, и для определения работы этой силы на конечном перемещении тела.

- Обобщённые координаты и обобщённые силы. Указать способы вычисления обобщённых сил.

- Обобщенные координаты. Число степеней свободы. Конфигурационное пространство.

- Обобщенные силы. Способы их определения.

- Обобщенный интеграл энергии.

- Обосновать формулы элементарной и полной работы переменной силы в случае криволинейной траектории движения точки. Дать определение и записать формулу мощности силы.

- Опишите последовательность решения второй задачи динамики точки. Что такое начальные условия движения точки?

- Опишите последовательность решения первой задачи динамики точки.

- Основы теории малых колебаний около положения устойчивого равновесия. Сформулировать теорему Лагранжа–Дирихле.

- Получить дифференциальное уравнение вращательного движения твёрдого тела.

- Получить дифференциальные уравнения плоско-параллельного движения твёрдого тела.

- Получить дифференциальные уравнения поступательного движения твёрдого тела.

- Получить закон сохранения полной механической энергии.

- Получить общее уравнение динамики.

- Получить основные свойства внутренних сил механической системы.

- Потенциальные силовые поля. Работа силы в потенциальном поле.

- Преобразование моментов инерции при параллельном переносе осей.

- Преобразование тензора инерции при повороте координатных осей.

- Прецессия тяжелого гироскопа. Гироскопический момент.

- Применение уравнений Лагранжа второго рода к системам с неудерживающими связями.

- Принцип возможных перемещений.

- Принцип Гамильтона-Остроградского для консервативных механических систем.

- Принцип Даламбера. Силы инерции.

- Принцип Даламбера-Лагранжа. Общее уравнение динамики.

- Рассмотреть задачу о движении материальной точки под действием восстанавливающей силы .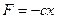

- Рассмотреть задачу о движении материальной точки под действием восстанавливающей силы 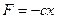и постоянной силы (силы тяжести).

- Рассмотреть задачу о движении материальной точки под действием восстанавливающей силы 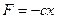и силы сопротивления 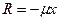, пропорциональной первой степени скорости, в случае .

- Рассмотреть задачу о движении материальной точки под действием восстанавливающей силы 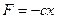и возмущающей силы в случае .

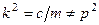- Рассмотреть задачу о движении материальной точки под действием восстанавливающей силы 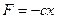и возмущающей силы в случае 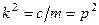(резонанс).

- Рассмотреть решение задачи о падении тела в сопротивляющейся среде. Как определить критическую скорость падения.

- Рассмотреть случай прямого удара тела о неподвижную поверхность. Коэффициент восстановления и его опытное определение.

- Рассмотреть частные случаи приведения сил инерции твердого тела в различных случаях его движения и записать соответствующие формулы.

- Свойства матрицы направляющих косинусов.

- Свойства моментов инерции: случай системы с материальной симметрией.

- Структура кинетической энергии механической системы.

- Структура уравнений Лагранжа второго рода.

- Сформулировать две основные задачи динамики материальной точки и изложить методы их решения.

- Сформулировать и доказать законы сохранения главных моментов количеств движения механической системы.

- Сформулировать и доказать теорему о главном моменте количеств движения механической системы. Сформулировать теорему Резаля.

- Сформулировать и доказать теорему о движении центра масс механической системы.

- Сформулировать и доказать теорему о кинетической энергии материальной точки в различных формах.

- Сформулировать и доказать теорему о кинетической энергии механической системы различных формах.

- Сформулировать и доказать теорему о количестве движения механической системы в различных формах.

- Сформулировать и доказать теорему о количестве движения точки в различных формах.

- Сформулировать и доказать теорему о моменте количества движения материальной точки. Рассмотреть движение точки под действием центральной силы.

- Сформулировать и доказать физический смысл диссипативной функции.

- Сформулировать определения действительного и возможного перемещения материальной точки и механической системы. Записать формулы для их вычисления.

- Сформулировать основные законы механики (законы Ньютона).

- Сформулировать принцип Даламбера для механической системы и обосновать метод кинетостатики.

- Сформулируйте второй закон Ньютона. Напишите в векторном виде основное уравнение динамики точки.

- Сформулируйте закон сохранения полной механической энергии системы.

- Сформулируйте законы сохранения количества движения системы.

- Сформулируйте законы сохранения момента количеств движения системы.

- Сформулируйте и запишите общее уравнение динамики в векторной и аналитической формах.

- Сформулируйте и запишите принцип возможных перемещений для механической системы.

- Сформулируйте и запишите принцип Даламбера для механической системы.

- Сформулируйте общие теоремы динамики.

- Сформулируйте определение и запишите формулу количества движения системы. Как связано количество движения системы с величиной и направлением скорости центра масс?

- Сформулируйте определение кинетической энергии системы. Как зависит кинетическая энергия системы от направления скоростей ее точек?

- Сформулируйте определение обобщенной силы.

- Сформулируйте определение связи. Какая связь называется стационарной, голономной, удерживающей?

- Сформулируйте основные задачи динамики.

- Сформулируйте основные законы динамики.

- Сформулируйте понятие мощности и запишите формулу для ее определения.

- Сформулируйте принцип возможных перемещений и докажите его достаточность.

- Сформулируйте принцип возможных перемещений и докажите его необходимость.

- Сформулируйте принцип возможных перемещений. Для каких условий применяется принцип возможных перемещений?

- Сформулируйте принцип Даламбера для материальной точки.

- Сформулируйте принцип Даламбера. Как определяются силы инерции?

- Сформулируйте теорему об изменении главного момента количеств движения материальной системы относительно точки и относительно оси.

- Сформулируйте теорему об изменении кинетической энергии системы в дифференциальной и в интегральной форме.

- Сформулируйте математическую постановку и изложите решение двух основных задач динамики точки.

- Сформулируйте, в чем заключаются первая и вторая задачи динамики точки?

- Тензор инерции однородного тонкого диска.

- Теорема о движении центра масс.

- Теорема об изменении кинетического момента механической системы относительно неподвижной точки.

- Теорема об изменении кинетического момента механической системы относительно центра масс.

- Теорема об изменении кинетического момента относительно произвольной точки.

- Теорема об изменении количества движения системы материальных точек.

- Углы Эйлера. Теорема Эйлера об определении взаимного положения двух систем координат.

- Уравнения Лагранжа второго рода в обобщенных координатах для консервативных механических систем. Функция Лагранжа.

- Уравнения Лагранжа второго рода в обобщенных координатах.

- Условия балансировки (отсутствия динамических реакций) твердого тела и их физический смысл.

- Циклические координаты. Циклические интегралы.

- Что называется потенциальной энергией и как определяется ее значение?

- Что называется элементарным импульсом и импульсом силы за конечный промежуток времени?

- Элементарная работа и мощность силы. Мощность системы сил, приложенных к твердому телу.

- Эллипсоид инерции. Главные оси инерции твердого тела.

Дата добавления: 2015-06-04