Рекомендации пользователю

В произведение

Тригонометрических функций

Формулы преобразования суммы

Функций в сумму

Произведения тригонометрических

Формулы преобразования

Формулы понижения степени

Двойного и тройного аргументов

Тригонометрические функции

Суммы и разности углов

Тригонометрические функции

Функциями одного аргумента

Тригонометрическими

Соотношения между

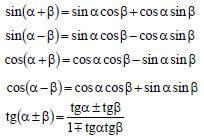
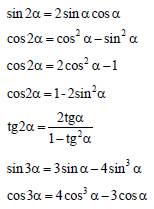
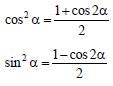
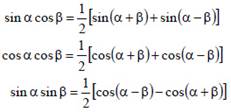
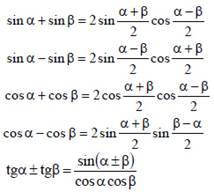
Глубокое и фундаментальное овладение основами физических знаний невозможно без самостоятельного систематического изучения курса физики по учебным пособиям.

В процессе изучения теоретического материала предполагается, что работа над учебником является основной и при этом рекомендуется вести краткий конспект, в котором указывается тема, рассматриваемый вопрос, формулировки, определения, схемы, выводы формул и типичные задачи. Но перед тем как приступить к этой работе, необходимо ознакомиться с основным содержанием и объемом знаний и умений по данной теме.

Следует также учитывать и то, что более качественному усвоению теоретического материала способствует работа по решению качественных и количественных задач. И, наоборот, уровень владения умениями и навыками решения задач по данной теме говорит об уровне ее усвоения.

Поэтому после изучения соответствующего теоретического материала необходимо рассмотреть данные в пособии задачи с решениями. Каждую из этих задач рекомендуется решить самостоятельно и сопоставить свое решение с решением, • приведенным в пособии. Затем необходимо решить задачи для самоподготовки, которые даны с ответами, и только после этого можно приступать к решению зачетных (контрольных) заданий. Задачи рекомендуется решать в такой последовательности:

Ознакомление с условием задачи и его запись. Условия записываются полностью, а ниже сокращенно.

Анализ задачи. В первую очередь необходимо выяснить физическую сущность задачи, а затем установить функциональную зависимость между величинами, данными в условии и величиной, которую необходимо найти. Чтобы лучше понять условие, следует сделать рисунок или схему. Заключительным этапом анализа задачи является выбор метода ее решения.

Решение задачи. Задачи можно решать аналитическим или синтетическим методом. Аналитический метод состоит в том, что сначала находят формулу, содержащую искомую величину и наибольшее количество величин, известных из условия задачи. Если в этой формуле имеются неизвестные величины, то чтобы выразить их через известные величины, необходимо использовать вспомогательные формулы. Подставив найденные выражения этих неизвестных величин в формулу искомой величины, мы получим формулу общего решений задачи.

Синтетический метод состоит в том, что решение задачи начинается не с искомой величины, а с величин, известных из условия. Используя известные связи между физическими величинами, данными в условии задачи, находим формулы, которые выражают функциональную зависимость между ними. В конечном итоге определяем искомую величину через ряд других величин, которые связаны с условием задачи.

Вычисление искомой величины. В правую часть формулы общего решения подставляем числовые значения физических величин с наименованиями, согласно Международной системе единиц СИ. Если формула общего решения сложна, то для проверки правильности решения правую часть сначала подставляются только наименования величин. Если наименование правой части совпадает с наименованием искомой величины, то решение задачи правильно. В противном случае в решении допущена ошибка. Вычисления следует выполнять с помощью калькулятора.

Объяснение решения задачи. Решение каждой задачи должно сопровождаться кратким объяснением, которое в строгой логической последовательности раскрывает ход рассуждений, ведущий к искомой величине.

Анализ результата. Получив искомую величину, необходимо проанализировать ее, чтобы убедиться в том, что она реальна и соответствует условию задачи.

Дата добавления: 2015-06-04