
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Картографические проекции
|
|
|
|
Картографическая проекция – это математически определенный способ изображения поверхности эллипсоида на плоскости, устанавливающий аналитическую зависимость между географическими координатами точек земного эллипсоида и прямоугольными координатами тех же точек на плоскости.
Картографические проекции обычно различают: 1) по характеру искажений; 2) по виду вспомогательной геометрической поверхности, применяемой при переходе от поверхности эллипсоида к плоскости (или по виду нормальной сетки); 3) по ориентировке этой поверхности по отношению к элементам земного эллипсоида (земной оси, экватору, полюсам).
По характеру искажений проекции делятся на равноугольные, равновеликие и произвольные (рис. 4).
Равноугольные - на карте отсутствуют искажения углов, а также формы бесконечно малых фигур. Масштаб длин в каждой точке постоянен по всем направлениям и зависит только от положения точки. Эллипсы искажений – окружности, увеличивающие радиус по мере удаления от места нулевых искажений.
Равновеликие − на карте отсутствуют искажения площадей. В этих проекциях площади эллипсов искажений равны. Увеличение масштаба длин по одной оси эллипса искажений компенсируется уменьшением масштаба длин по другой оси, что вызывает сильное искажение углов и форм.
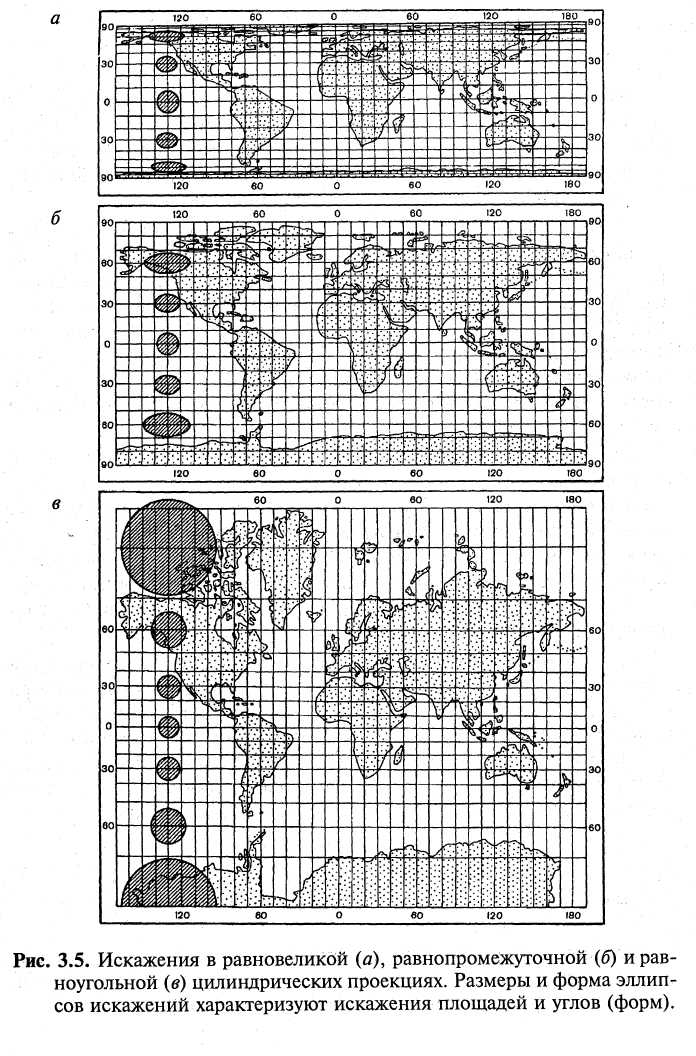 Произвольные − на карте имеются искажения и углов, и площадей. Карты, построенные в этих проекциях, отличаются меньшим искажением площадей, чем в равноугольных проекциях, и меньшим искажением углов и форм, чем в равновеликих проекциях. Среди произвольных проекций можно выделить равнопромежуточные проекции, во всех точках которых масштаб по одному из направлений (по параллелям или меридианам) постоянен и равен главному.
Произвольные − на карте имеются искажения и углов, и площадей. Карты, построенные в этих проекциях, отличаются меньшим искажением площадей, чем в равноугольных проекциях, и меньшим искажением углов и форм, чем в равновеликих проекциях. Среди произвольных проекций можно выделить равнопромежуточные проекции, во всех точках которых масштаб по одному из направлений (по параллелям или меридианам) постоянен и равен главному.
 а в
а в

б
Рис. 4. Искажения в равновеликой (а), равнопромежуточной (б) и равноугольной (в) цилиндрических проекциях
По виду вспомогательной геометрической поверхности различают цилиндрические, конические и азимутальные проекции.
Цилиндрическими называют проекции, в которых сеть меридианов и параллелей с поверхности эллипсоида переносится на боковую поверхность касательного или секущего цилиндра, затем цилиндр разрезается по образующей и развертывается в плоскость. В зависимости от ориентировки цилиндра относительно земной оси различают проекции:
а) нормальные, когда ось цилиндра совпадает с малой осью земного эллипсоида. Сетка: меридианы представляют собой равноотстоящие друг от друга параллельные прямые линии; параллели – прямые, перпендикулярные меридианам. Линия нулевых искажений – экватор. Поэтому в этих проекциях строят карты территорий, вытянутых вдоль экватора, или карты мира.
б) поперечные, когдаось цилиндра лежит в плоскости экватора (т. е. перпендикулярна малой земной оси). Линия нулевых искажений – меридиан касания. Сетка: параллели и меридианы – кривые линии.
в) косые, когдаось цилиндра составляет с осью эллипсоида острый угол. Линия нулевых искажений – линия касания цилиндра и эллипсоида. Сетка: параллели и меридианы – кривые линии.
Проекции, построенные на касательном цилиндре, имеют одну линию нулевых искажений, а проекции, построенные на секущем цилиндре, – две линии нулевых искажений (рис. 5).
Коническими называют проекции, в которых сеть меридианов и параллелей с поверхности эллипсоида переносится на боковую поверхность касательного или секущего конуса, затем конус разрезается по образующей и развертывается в плоскость. В зависимости от ориентировки конуса относительно земной оси различают проекции:
а) нормальные, когдаось конуса совпадает с малой осью земного эллипсоида. Сетка: меридианы представляют собой прямые линии, расходящиеся из вершины конуса; параллели – дуги концентрических окружностей. Линия нулевых искажений – любая параллель касания, кроме экватора. Поэтому в этих проекциях строят карты территорий, вытянутых вдоль параллели касания. Например, карты России.
б) поперечные, когдаось конуса лежит в плоскости экватора (т. е. перпендикулярна малой земной оси). Линия нулевых искажений – меридиан касания. Сетка: параллели и меридианы – кривые линии.
в) косые, когдаось конуса составляет с осью эллипсоида острый угол. Линия нулевых искажений – линия касания. Сетка: параллели и меридианы – кривые линии.
Два последних вида проекций употребляются очень редко.
 а б
а б

в

г
Рис. 5. Цилиндрические проекции (а – развертка нормальной цилиндрической проекции на касательном цилиндре; б – нормальная цилиндрическая проекция на секущем цилиндре; в – поперечная цилиндрическая проекция на касательном цилиндре; г – косая цилиндрическая проекция на секущем цилиндре)
Проекции, построенные на касательном конусе, имеют одну линию нулевых искажений, а проекции, построенные на секущем конусе, – две линии нулевых искажений (рис. 6).


а б
Рис. 6. Нормальная коническая проекция (а – проекция на касательный конус и развертка; б – проекция на секущий конус и развертка)
Азимутальными называют проекции, в которых сеть параллелей и меридианов переносится с поверхности эллипсоида на касательную (или секущую) картинную плоскость. Точка касания плоскости и земного эллипсоида является точкой нулевых искажений. В зависимости от положения точки касания, среди азимутальных проекций различают простые:
а) полярные (нормальные), когдаплоскость касается земного эллипсоида в одном из полюсов. Сетка: параллели – концентрические окружности с центром в точке полюса; меридианы – прямые линии, радиусы этих окружностей. Используются для построения карт Антарктиды и Северного Ледовитого океана.
б) экваториальные (поперечные), когдаплоскость касается эллипсоида в любой точке на экваторе. Сетка: средний меридиан и экватор − взаимно перпендикулярные прямые линии, остальные параллели и меридианы – кривые линии (иногда параллели изображаются прямыми линиями). В этих проекциях строят карты полушарий и Африки.
в) горизонтальные (косые), когдаплоскость касается эллипсоида в какой-либо точке, лежащей между полюсом и экватором. Сетка: средний меридиан, на котором расположена точка касания, – прямая линия; остальные меридианы и параллели – кривые линии. Эти проекции используются при построении карт материков, когда точка нулевых искажений находится в центре изображаемого материка (рис. 7).
а б

в г


Рис. 7. Азимутальные проекции (а – нормальная проекция на плоскость; б – сетка в нормальной проекции; в – сетка в поперечной проекции; г – сетка в косой проекции)
В зависимости от положения центра проектирования (точки зрения) среди азимутальных проекций выделяют перспективные (рис.8):
а) центральные (гномонические) - центр проектирования расположен в центре Земли.
б) стереографические - центр проектирования расположен на конце диаметра Земли, противоположном точке касания.
в) внешние - центр проектирования находится вне поверхности Земли, но на определенном расстоянии.
г) ортографические - центр проектирования удален в бесконечность.
Поликоническими называют проекции, в которых проектирование сети параллелей и меридианов производится сразу на несколько конусов. Сетка: центральный меридиан и экватор – взаимно перпендикулярные прямые линии, остальные параллели – дуги эксцентрических окружностей, а меридианы – кривые линии (рис. 9). Используются при построении карт мира.
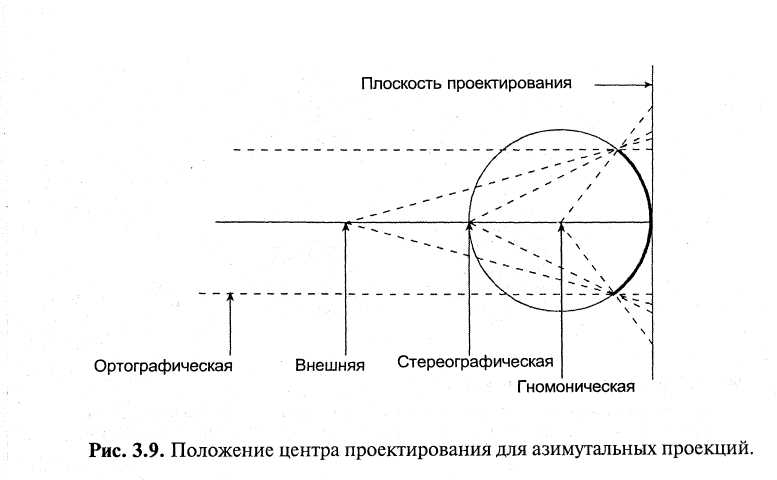
Рис. 8. Положение центра проектирования для азимутальных перспективных проекций
Условными называют проекции, при построении которых не прибегают к использованию вспомогательной геометрической поверхности. Сеть параллелей и меридианов строят исходя из каких-либо заданных условий. К условным проекциям принадлежат псевдоцилиндрические, псевдоконические, псевдоазимутальные и другие проекции, полученные путем преобразования исходных проекций (рис. 9).

а б в г
Рис. 9. Вид сетки меридианов и параллелей в разных картографических проекциях (а – псевдоцилиндрическая; б – псевдоконическая; в – поликоническая; г – псевдоазимутальная)
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 3245; Нарушение авторских прав?; Мы поможем в написании вашей работы!