Силы называют сходящимися, если их линии действия пересекаются в одной точке

Геометрический метод сложения сил

Плоская система сходящих сил.

Различают плоскую систему сходящихся сил, когда линии действия всех данных сил лежат в одной плоскости, и пространственную систему сходящихся сил, когда линии действия сил лежат в разных плоскостях. На основании следствия из третьей аксиомы, силу можно переносить по линии ее действия. Поэтому сходящиеся силы всегда можно перенести в одну точку — в точку пересечения их линий действия. Выполнив перенос, получим четыре силы:F1,F2,F3,F4, приложенные к точке С. Для определения их равнодействующей сложим последовательнов все данные силы, используя правило треугольника.

Находим частичные равнодействующие:

И, наконец, сложив все силы, определяем полную равнодействуюшую:

Промежуточные векторы можно не строить, а последовательно, в указанном выше порядке одну за другой отложить все заданные силы и начало первой соединить с концом последней. Фигура OABCD называется силовым многоугольником. Замыкающая сторона этого многоугольника представляет собой равнодействующую 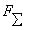заданной системы сил, равную их геометрической сумме. Необходимо обратить внимание на то, что равнодействующая сила 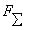всегда направлена от начала первого слагаемого к концу последнего слагаемого. Иными словами, стрелка равнодействующей силы всегда направлена навстречу обхода многоугольника, соответствующему последовательному сложению заданных сил.

Когда при построении силового многоугольника конец последней слагаемой силы совместится с началом первой, равнодействующая F2 системы сходящихся сил окажется равной нулю. В этом случае система сходящихся сил находится в равновесии.

Самозамыкание силового многоугольника данной системы сходящихся сил является геометрическим условием ее равновесия.

1.2.2 Проекция силы на ось

Решение задач на равновесие сходящихся сил с помощью построения замкнутых силовых многоугольников в большинстве случаев сопряжено с громоздкими построениями. Более общим и универсальным методом решения таких задач является переход к определению проекций заданных сил на координатные оси и оперирование с этими проекциями. Осью называют прямую линию, которой приписано определенное направление. Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными на нее из начала и конца вектора.

Проекция вектора считается положительной (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси.
Проекция вектора считается отрицательной (—), если направление от начала проекции к ее концу противоположно положительному направлению оси.

Рассмотрим ряд случаев проецирования сил на ось:

• Вектор силы F составляет с положительным направлением оси х острый угол а. Чтобы найти проекцию, из начала и конца вектора силы опускаем перпендикуляры на ось х; получаем: . Проекция вектора в данном случае положительна.
• Сила F составляет с положительным направлением оси х тупой угол а. Тогда,
  т. е. Fx = — F*cos р. Проекция силы F на ось х в данном случае отрицательна.
• Сила F (рис.12,в) перпендикулярна оси х. Проекция силы F на ось х равна нулю, т.е. Fx — F cos 90° = 0.

Дата добавления: 2015-06-04