Введение 2 страница. В случае шестиэлектродного и восьмиэлектродного электростатических подвесов проводится сравнение возмущающих моментов высших гармоник

В случае шестиэлектродного и восьмиэлектродного электростатических подвесов проводится сравнение возмущающих моментов высших гармоник, возникающих при наличии в форме тела гармоник одинаковой амплитуды.

Рассматривается задача о выборе оптимального радиуса ротора, минимизирующего угловую скорость ухода электростатического гироскопа, вызванного наличием первой и второй гармоник в форме ротора.

Для описания и анализа моментного взаимодействия в неконтактном подвесе используются также теоретико-вероятностные методы. Поверхность взвешенного в неконтактном подвесе тела рассматривается как реализация некоторого случайного поля. При этом устанавливается связь вероятностных характеристик возмущающих моментов со статистическими оценками качества поверхности тел. Знание такой связи имеет большое практическое значение, так как позволяет, не проводя детального анализа поверхности, оцепить вероятный уровень возмущающих моментов, действующих на твердое тело в неконтактном подвесе. Предполагается, что поверхность тела, взвешенного в неконтактном подвесе, близка к сферической и может рассматриваться как случайное поле па сфере с нулевым математическим ожиданием и известной корреляционной функцией. Определяется зависимость дисперсии возмущающего момента от параметров неконтактного подвеса.

Гл. III монографии посвящена анализу динамики твердого тела в неконтактном подвесе в случае, когда поверхность тела есть сфера, а центр масс не совпадает с центром сферической поверхности твердого тела. При этом из-за взаимосвязи движения центра масс и углового движения твердого тела вокруг центра масс возникает ряд механических эффектов, исследование которых и является целью гл. III. Предполагается, что поддерживающие силы в неконтактном подвесе действуют по нормали к поверхности тела, и, следовательно, приводятся к равнодействующей, приложенной в геометрическом центре твердого тела. Равнодействующая «притягивает» геометрический центр шара к некоторой неподвижной точке пространства О, которая называется центром неконтактного подвеса. Твердое тело предварительно раскручено вспомогательной системой и в рабочем режиме вращается по инерции. Силы сопротивления движению отсутствуют - тело находится в вакууме. Разделение быстрых и медленных движений в рассматриваемой задаче проводится при помощи общей схемы осреднения, причем правые части уравнений для медленных переменных осредняются как по движению Эйлера - Пуансо, так и по движению центра масс твердого тела.

Показано, что взаимосвязь поступательных и вращательных движений несбалансированного шара может приводить как к торможению, так и к разгону твердого тела, т. е. неконтактный подвес может выполнять роль своеобразного двигателя, регулирующего угловую скорость вращения тела. Найдены условия, которым должна удовлетворять передаточная функция следящей системы неконтактного подвеса, чтобы обеспечить существование стационарных вращений несбалансированного шара. Определены условия устойчивости нутационных колебаний твердого тела и проведены оценки амплитуды биений несбалансированного шара в неконтактном подвесе. Обсуждается механизм возникновения тормозящих или ускоряющих моментов в неконтактном подвесе.

Далее в гл. III исследуется динамика несбалансированного шара в неравножестком подвесе, установленном на равномерно вращающемся основании. Проводится анализ выражений для моментов, действующих на тело в случае, когда ось динамической симметрии тела близка к вектору кинетического момента. Оказывается, что силовая функция потенциальной части моментов, приложенных к несбалансированному шару в неконтактном подвесе, является однородной квадратичной формой направляющих косинусов оси динамической симметрии тела, т. е. потенциальная часть моментов будет аналогична моменту, вызываемому наличием второй гармоники в форме тела. Непотенциальная часть моментов в неравножестком подвесе может приводить к разгону (или торможению) шара, а также к изменению положения вектора кинетического момента в инерциальном пространстве. Найдена зависимость углового ускорения твердого тела от ориентации вектора кинетического момента относительно осей, жестко связанных с неконтактным подвесом.

Исследуется динамика твердого тела в неконтактном подвесе, установленном на вибрирующем основании. Предполагается, что подвес равножесткий, а основание совершает гармонические поступательные колебания вдоль неизменно ориентированной в пространстве оси. При помощи соответствующих результатов теории асимптотических методов, относящихся к резонансным задачам, построены осредненные уравнения для расширенного вектора медленных переменных. (Кроме переменных, определяющих положение вектора кинетического момента твердого тела, вводится дополнительная медленная переменная - так называемая фазовая расстройка.) Анализ осредненных уравнений показывает, что вибрация оказывает влияние па движение твердого тела только в тех случаях, когда частота вибрации основания близка к одной из частот углового движения твердого тела.

Проводится исследование стационарных резонансных режимов движения твердого тела в неконтактном подвесе при поступательной однокомпопентной вибрации основания. Обсуждается возможность синхронизации частоты вращения тела с частотой вибрации основания.

Более подробно рассмотрен случай консервативного подвеса (такой случай может иметь место в неконтактных подвесах, у которых равнодействующая силового поля пропорциональна смещению геометрического центра шара из центра подвеса - так называемый «чисто упругий подвес»). В консервативном подвесе для осредненных уравнений движения удается найти три первых интеграла, которых достаточно для того, чтобы свести задачу к квадратурам. Указанные интегралы аналогичны интегралам задачи о резонансных движениях динамически симметричного спутника в гравитационном поле [18]. Отличие состоит только в структуре силовой функции, поэтому исследование осредненных уравнений можно провести методами, изложенными в монографии В. В. Белецкого [18]. Анализ резонансных движений несбалансированного шара позволил получить формулы для ухода вектора кинетического момента.

Исследуется движение несбалансированного шара с произвольным эллипсоидом инерции. Вместо медленной переменной угла нутации J вводится медленная переменная k ₂, которая является модулем эллиптических функций Якоби, описывающих движение твердого тела около центра масс в случае Эйлера - Пуансо. В случае, когда параметр k ₂ мал, что соответствует малым колебаниям оси наибольшего или наименьшего моментов инерции твердого тела вблизи вектора кинетического момента, в нерезонансной ситуации построены осредненные уравнения движения твердого тела в неконтактном подвесе. Из этих уравнений найдены условия устойчивости вращения твердого тела вокруг осей наибольшего и наименьшего моментов инерции тела.

Изучается влияние нелинейности неконтактного подвеса на движение несбалансированного шара. Обнаружено явление ухода вектора кинетического момента, вызванного нелинейностью подвеса. Получено необходимое и достаточное условие интегрируемости прецессионных уравнений движения твердого тела под действием только неконсервативных моментов. Построены траектории движения вектора кинетического момента для частных случаев нелинейности подвеса.

В заключение в гл. III исследуется динамика несбалансированного шара в неконтактном подвесе с импульсной системой регулирования. Необходимость подобного исследования связана с широким применением импульсных систем при конструировании новых типов неконтактных подвесов [207, 214]. Оказывается, что и в случае импульсного управления имеют место многие механические эффекты, найденные в случае непрерывного управления: существование стационарных скоростей вращения шара, возможность изменения амплитуды нутационных колебаний и т. п.

В гл. IV сформулирована задача исследования совместной системы уравнений электродинамики, записанных в квазистационарном приближении, и уравнений движения твердого тела вокруг центра масс. Определяются классы движений, для которых возможно построение асимптотического решения задачи. В случае малой глубины проникновения магнитного поля в проводник перед оператором Лапласа в уравнении параболического типа для вектора напряженности магнитного поля возникает малый параметр. Для решения электродинамической задачи применяется метод пограничного слоя. Показано, что решение задачи движения твердого тела в магнитном поле разбивается на две части. Первая, электродинамическая часть задачи сводится к решению некоторых стандартных краевых задач, зависящих от формы области, занятой проводящим материалом тела, и не зависящих от движения тела, и затем к подсчету компонент тензоров, определяемых на решении указанных стационарных краевых задач. Вторая часть задачи сводится к решению уравнений движения твердого тела и не требует решения уравнений с частными производными. Такое разбиение позволяет существенно упростить исходную задачу. Так, в случае малой глубины проникновения поля в проводник задача о движении твердого тела произвольной формы в магнитном поле сводится к исследованию некоторого интегродифференциального уравнения.

В качестве иллюстрации использования построенного интегродифференциального уравнения рассматривается задача о плоских колебаниях относительно горизонтальной оси тяжелого твердого тела сферической формы, находящегося в высокочастотном однородном магнитном поле. В указанной задаче обнаружен эффект нарастания амплитуды колебаний тела.

При анализе электродинамической задачи другой предельный случай - случай большой глубины проникновения поля в проводник - возникает при медленных движениях тела относительно поля. Здесь малый параметр появляется при производной по времени в параболическом уравнении для вектора напряженности магнитного поля, а пограничный слой развивается вдоль временной оси. При помощи методов сингулярных возмущений и в этом случае нестационарная электродинамическая задача сводится к решению серии стационарных краевых задач, зависящих лишь от формы тела. При этом удается установить аналогию между задачей расчета тензоров поляризуемости проводящего твердого тела и задачей расчета тензора присоединенных моментов инерции, возникающих при исследовании движения твердого тела с полостями, содержащими жидкость. В случае осесимметричного внешнего поля, в котором находится твердое тело, определяется структура момента сил, действующих на тело.

В конце гл. IV рассматривается задача построения двусторонних оценок момента сил в магнитном поле. Развитый в гл. IV асимптотический подход для определенных, заранее обусловленных классов движения существенно расширяет возможности отыскания приближенного выражения для момента сил, действующих на проводящее твердое тело. Вместе с тем аналитическое решение построенных стационарных краевых задач известно далеко не всегда, а численные алгоритмы громоздки и требуют больших затрат машинного времени. Поэтому представляет интерес получение эффективных двусторонних оценок для тензоров поляризуемости тела, компоненты которых представляют собой функционалы на решениях стационарных краевых задач. В книге с помощью методов теории двойственности [68, 144] получены верхние и нижние оценки диагональных компонент тензоров поляризуемости и, следовательно, оценены моменты сил, действующих на проводящее твердое тело в магнитном поле. Кроме того, использование методов выпуклого анализа позволило сформулировать экстремальные принципы для диссипации энергии истинных токов в проводящей среде и энергии магнитного поля, создаваемого вихревыми токами, индуцированными в проводнике.

Установление эквивалентности традиционной постановки задачи в терминах краевых задач для систем дифференциальных уравнений и проблемы экстремума функционалов, являющихся диагональными компонентами тензоров поляризуемости, существенно расширяет возможности решения задач динамики твердого тела произвольной формы в магнитном поле. Полученные неравенства могут быть применены и для двусторонних оценок диагональных элементов тензора присоединенных моментов инерции в задаче Стокса - Жуковского о вращении тела с полостью, целиком заполненной идеальной жидкостью.

Гл. V посвящена исследованию механических задач. возникающих при рассмотрении движения проводящего твердого тела произвольной формы в однородном магнитном поле при большой глубине проникновения поля в проводник. В случае, когда кинетическая энергия тела велика по сравнению с моментом сил, создаваемых магнитным полем, при помощи метода осреднения построены эволюционные уравнения для медленных переменных задачи. В качестве порождающего решения общей схемы осреднения используется известное решение Эйлера - Пуансо движения твердого тела около неподвижной точки, которое рассматривается как нулевое приближение к искомому возмущенному движению. В качестве примера использования построенных осредненных уравнений рассматривается задача о влиянии вихревых токов на вращение и ориентацию спутника. Показывается, что при угловых скоростях вращения спутника, меньших его орбитальной скорости, момент от вихревых токов может приводить к раскрутке спутника. Определяются стационарные вращения спутника и исследуется их зависимость от наклонения плоскости орбиты и соотношения между компонентами тензора поляризуемости спутника. Устанавливается аналогия между моментом от вихревых токов и моментом приливных сил, действующих на деформируемое небесное тело в гравитационном поле притягивающего центра. Анализируется существование и устойчивость стационарных вращений небесного тела в зависимости от соотношения между компонентами тензора приливного момента.

В качестве другого приложения рассматриваемой задачи в гл. V исследуется раскрутка ротора неконтактного гироскопа вращающимся магнитным полем. Анализ осредненных уравнений показывает, что вектор кинетического момента стремится совпасть с осью вращения магнитного поля. В случае, когда эллипсоид инерции ротора сжат, ось динамической симметрии ротора стремится совпасть с вектором кинетического момента. В случае вытянутого эллипсоида инерции окончательным движением будет вращение вокруг оси, перпендикулярной оси динамической симметрии. В случае, когда коэффициенты поляризуемости ротора относительно главных осей инерции не равны между собой, обнаружено существование критического значения вектора кинетического момента гироскопа, при котором скорость изменения угла нутации обращается в нуль, а угол нутации достигает своего экстремального значения.

Рассматривается процесс раскрутки ротора неконтактного гироскопа вращающимся магнитным полем с учетом сопротивления среды. Определяются условия устойчивости стационарного вращения ротора гироскопа как в резонансном, так и в нерезонансном случаях. Рассмотрены стационарные режимы, допускаемые осредненными уравнениями, полученными в нерезонансном случае. Найдены области в пространстве параметров, в которых возможно существование устойчивых регулярных прецессий ротора гироскопа.

Исследуется устойчивость стационарных вращений твердого тела с произвольным эллипсоидом инерции во вращающемся и постоянном магнитных полях. Анализ корней характеристического уравнения позволяет оценить быстроту затухания угловых колебаний твердого тела и рассмотреть вопрос о выборе моментов инерции тела, обеспечивающих наиболее быстрое приведение оси наибольшего момента инерции тела к оси вращения магнитного поля в силу линеаризованной системы уравнений.

В конце гл. V изучено некоторое резонансное движение динамически симметричного твердого тела во вращающемся магнитном поле. Это движение представляет собой регулярную прецессию, при которой вектор кинетического момента тела направлен по оси вращения поля, а ось симметрии тела совпадает с вектором напряженности магнитного поля (в этом случае возникает резонанс 1:1 между частотой прецессии и частотой вращения магнитного поля). Характеристическое уравнение для линеаризованной системы уравнений имеет нулевые корни, и анализ устойчивости указанной регулярной прецессии при помощи методов теории критических случаев [119] позволяет сделать вывод о неустойчивости по Ляпунову найденного резонансного движения.

В гл. VI анализируется динамика твердого тела, имеющего проводящую область, обладающую сферической симметрией, при произвольной глубине проникновения магнитного поля в проводник. В случае быстрых вращений твердого тела удается провести разделение быстрых и медленных составляющих движения в совместной системе уравнений электродинамики и твердого тела. При этом электродинамическая часть задачи сводится к известной стационарной краевой задаче, допускающей для сферы или сферической оболочки решение стандартным методом разделения переменных. Механическая часть задачи после процедуры осреднения в нерезонансном случае сводится к исследованию нелинейных уравнений движения твердого тела, записанных в оскулирующих переменных.

Выписываются осредненные уравнения, построенные в случаях движения в однородном постоянном, переменном и вращающемся магнитных полях как динамически симметричного твердого тела, так и твердого тела с произвольным эллипсоидом инерции при малых отклонениях оси наибольшего момента инерции тела от вектора кинетического момента. В случае переменного магнитного поля указывается на возможность существования ускоряющего момента и стационарных движений, при которых ось симметрии тела не совпадает с вектором кинетического момента. Кроме того, определяются стационарные режимы движения твердого тела, представляющие собой медленные прецессии вектора кинетического момента вокруг направления, вдоль которого изменяется сектор напряженности магнитного поля.

В случае вращающегося магнитного поля найдены условия убывания амплитуды нутационных колебаний твердого тела. Определено движение шарового гироскопа при малых отклонениях оси симметрии ротора от оси статора двигателя.

Автор надеется, что предлагаемая книга может оказаться полезной для специалистов, разрабатывающих электромеханические системы различных назначений.

Движение упругого ротора с произвольном эллипсоидом инерции в неконтактном подвесе.

3.1. построение уравнений движения тела с произвольном эллипсоидом инерции

Рассмотрим ротор электростатического гироскопа с произвольным эллипсоидом инерции. Пусть ξ, х, η, по – прежнему, правые ортогональные трехгранники с началом в центре масс тела – точке О (рис 2.1), имеющие тот же смысл, что и в главе 2.

Уравнение (2.4), не замкнуто, так как содержит два неизвестных вектора L и ω. Для получения замкнутой системы уравнений выпишем в матричной форме кинематические уравнение Пуассона:

Ѓ = Г * ὣ, (3.1)

, ,

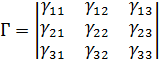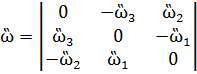где Г – матрица направляющих косинусов между осями трехгранников η и х, так что

η=Г* х (3.2)

В качестве порождающего решения уравнения движения тела относительно центра масс используем известное решение Эйлера-Пуансо движение твердого тела около неподвижной точки. Допустим, что I₁˂I₂˂I₃. Будем рассматривать невозмущенное движения при условии 2ТI₂ ≤L² ≤ 2TI₃ (Т – кинетическая энергия ротора относительно центра масс), что соответствует траекториям вектора кинетического момента, охватывающим ось х ₃. Тогда согласно из (2.4) получим

, ,

, ,

,

, ,

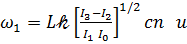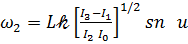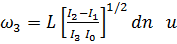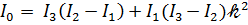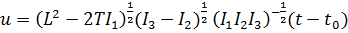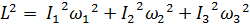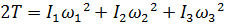где cn u, sn u, dn u – эллиптические функции якобы, модуль которых 𝓀² определяется формулой

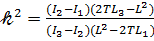. (3.4)

Проекции вектора кинетического момента L тела на оси х₁ х₂ х₃ имеют вид

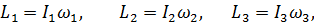
и направляющие косинусы между осью η₃, направленной по вектору L, и осями х₁ х₂ х₃ определяются как

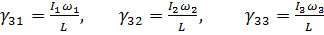(3.5)

Рассмотрим такие движения твердого тела, при которых ось х₃ совершает малые колебания вблизи вектора кинетического момента L твердого тела, следовательно, параметр 𝓀² мал по сравнению с единицей.

Выпишем разложение по параметру 𝓀² решения уравнения (2.4). При 𝓀²=0 из (3.3) получим ω₁= ω₂=0, ω₃=L/I₃, и тело совершает равномерное вращение вокруг оси х₃ совпадающей с осью η₃.

Для нахождения членов первого порядка малости по 𝓀 рассмотрим динамические уравнения Эйлера (2.4), в которых ω₃ постоянная, а ω₁,ω₂ считаются величинами первого порядка малости и, имеем

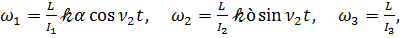(3.6)

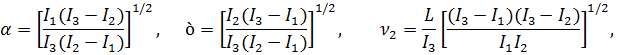
Как следует из 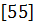, коэффициенты матрицы Г (3.1) при разложении по малому параметру 𝓀 с точностью до 𝓀² определяется выражениями

,

,

.

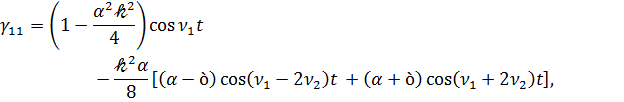
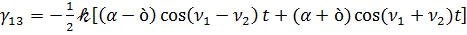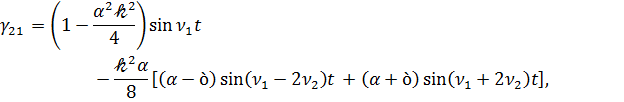
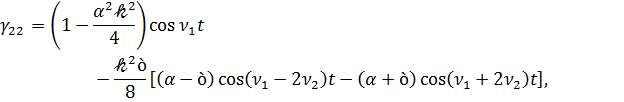
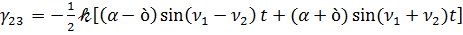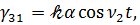
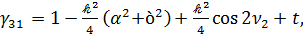
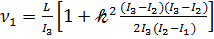3.2. Определение деформаций ротора, вызванных инерционными силами

Удельная величина вектора инерционных сил F, возникающих при вращении ротора, определяеться формулой (2.9).

Запишем проекции вектора F на очи трехгранника х₁ х₂ х₃, с учетом (3.6)

,

,

,

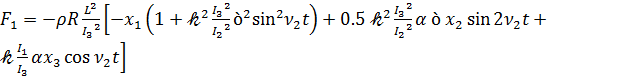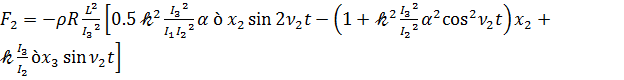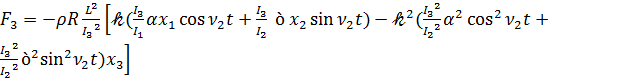С учетом (2.10) перепишем уравнения (3.8) и после некоторых выкладок, получим

,

,

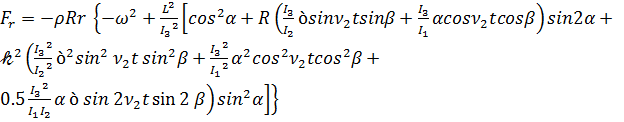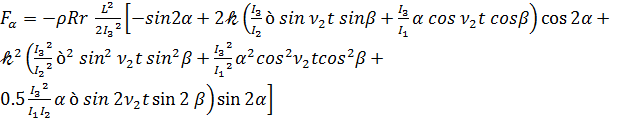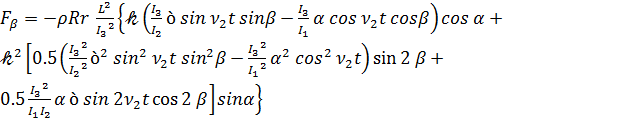(3.9)

Как и в главе 2, силы (3.9) являются потенциальными и определяются выражением (2.12), при этом параметр ᴂ в полиноме Лежандра имеет вид

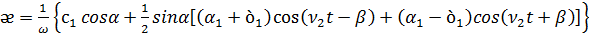(3.10)

где , , .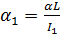

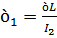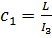Формулу для полинома Лежандра Р (ᴂ), учитывая (3.10), можно представить так

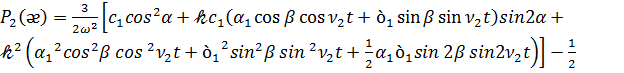(3.11)

Решая квазистационарную задачу теория упругости (2.13) с граничным условием (2.14), найден вектор перемещений u (u_r u_α u_β) точек ротора, вызванных наличием инерционных сил (3.9).

Так же как в главе 2, при решении (2.13), (2.14) будем пренебрегать изменением плотности в экваториальной плоскости ротора и ограничимся нахождением перемещений для однородного шара.

Выражение для компонент вектора перемещений в рассматриваемом случае в сферической системе координат r, α, β с точностью до обозначений совпадает с выражением (2.21), полученным для динамически симметричного ротора, только в этих уравнениях вместо полинома, определяемого формулой (2.21), следует подставить полином (3.11)

3.3. Определение постоянной времени затухания нутационных колебаний

Дифференцируя формулы (2.21) по времени, учитывая (3.11), находим компоненты относительной скорости точек ротора гироскопа

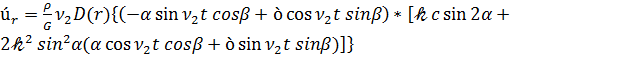, (3.12)

,

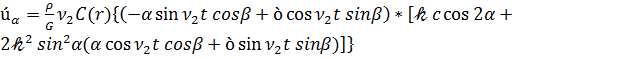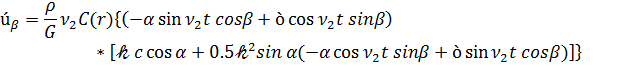
где функции D(r) и C(r) те же, что и формулах (2.23)

Для оценки потерь энергии так же, как и в главе 2, предположим, что внутренне трение в материале подчиняется гипотезе Кельвина-Фойгта, и введем диссипативную функция Рэлея по формуле (2.24)

Воспользовавшись соотношениями (2.25), выражающими тензор деформации через производные от компонент вектора перемещений в сферических координатах r, α, β с учетом (3.12), для скорости тензора деформации имеем

,

,

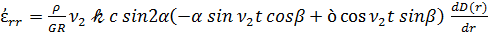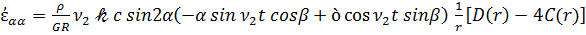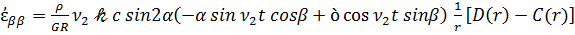(3.13)

,

,

,

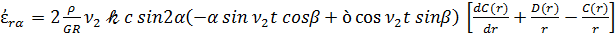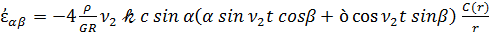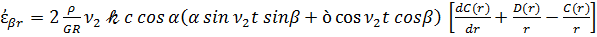Представляя (3.13) в (2.24) и выполняя необходимые вычисления, находим диссипативную функцию Рэлея

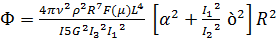, (3.14)

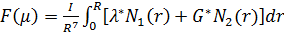, (3.15)

,

,

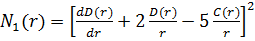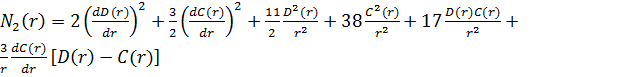В качестве оценки коэффициента вязкого трения воспользуемся формулой (2.36).

Введем функцию 𝓀² (0≤𝓀2≤1), определяемую формулой (3.4) и однозначно связанную с энергией тела Т. Значение 𝓀² = 0 соответствует вращению тела вокруг оси х₃, а 𝓀² = 1 – движению по сепаратрисе.

Функция 𝓀², так же как модуль кинетического момента L и кинетическая энергия Т, есть медленно меняющаяся переменная. Дифференцируя формулу (3.4) по времени, получаем

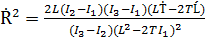(3.16)

Предположим так же, как и в главе 2, что момент внешних сил относительно центра масс ротора гироскопа равен нулю (L=const). Скорость убывания механической энергии системы равняется удвоенной диссипативной функции Ф, поэтому, принимая во внимание (3.14) и (3.16), приходим к следующему дифференциальному уравнению для функции 𝓀²

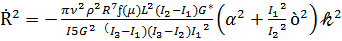, (3.17)

Подстановка параметра G^*, определяющего внутреннее трение (2.36), в выражение постоянную времени приводит к следующему окончательному уравнению

Дата добавления: 2015-06-04