Введение 3 страница. Числовой пример 3.1. Рассмотрим электростатический гироскоп со сплошным бериллиевым ротором, физические и геометрические размеры к

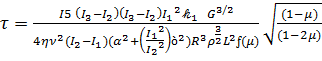, (3.18)

Где

,

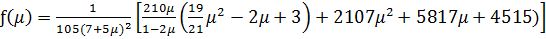Числовой пример 3.1. Рассмотрим электростатический гироскоп со сплошным бериллиевым ротором, физические и геометрические размеры которого описаны в примере 2.1. Номинальная угловая скорость ω=1.88*10⁴ сек^-1, I₁=0.9*I, I₂=0.95I, I₃=I, α²=0.9, ò²=1.9, ν²=0.058*ω², логарифмический декремент затухания η=0.02. В этом случае из (3.18) для постоянной времени получаем 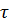=205 часов.

Числовой пример 3.2. Теперь рассмотрим ЭСГ со сплошным алюминиевым ротором. Физические и механические характеристики оставим таким же, как и в примере 2.22 Тогда из (3.18) находим что 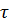=20.3 час.

3.4. Возмущающие моменты, вызванные упругими деформациями ротора.

Полагая в первом уравнений системы (2.21) r=1, получим, учитывая (3.11), уравнение деформации ротора в сферической системе координат, жестко связанной с ротором

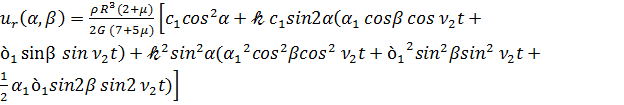
Переход от неподвижных осей ξ _i к подвижным х_i совершается при помощи следующего соотношения

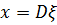
Здесь элементы δ _{i j} матрицы D определяются при помощи матричных преобразований (2.2) и (3.2)

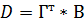
Предположим, что вектор кинетического момента лежит в плоскости ξ₁ ξ₃, т.е. ξ=0, тогда для направляющих косинусов трехгранника ξ_i в х₁ х₂ х₃ получим следующее выражения

,

,

,

,

,

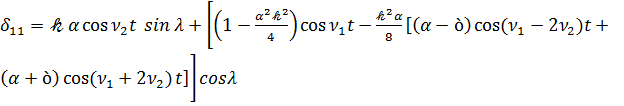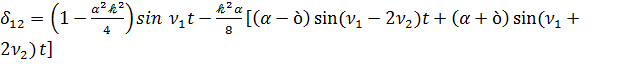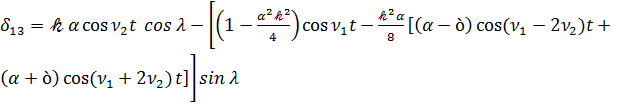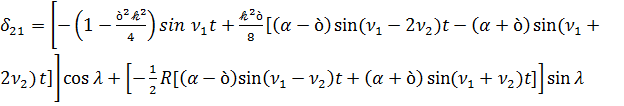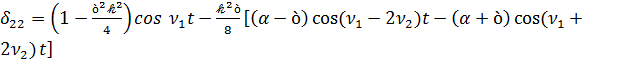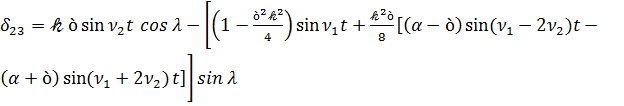, (3.21)

,

,

,

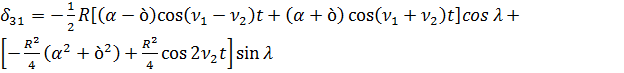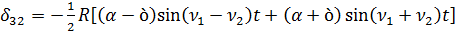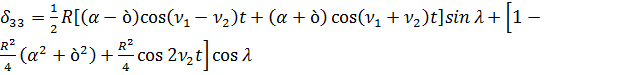С учетом (3.21) получим уравнение деформированной поверхности ротора в трехграннике ξ₁ ξ₂ ξ₃ жестко связанном с корпусом ротора в сферических координатах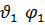

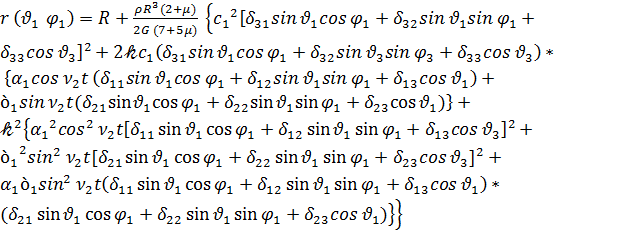, (3.22)

Далее проводим асферизацию ротора, как это делалось во второй главе. Это означает, что в (3.22) первое слагаемое с множителем с₁², следует положить равным нулю.

Подставляя уравнение (3.22) в формулу (2.67) и выполняя интегрирование по поверхностям электродов (2.68), затем осредняя полученные выражения по явно входящему времени с учетом (3.21) имеем для проекции момента поддерживающих сил, действующих со стороны пятого и шестого электродов следующие выражения:

,

,

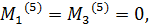
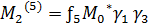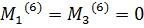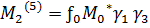
где

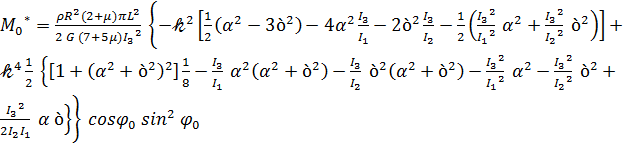, (3.24)

Заметим, что уравнения (3.23) совпадают по структуре с уравнениями (2.74), однако, М₀ в (2.74) следует заменить на М₀^*, следовательно, выражение силовой функции для моментов сил (2.81) полученные при анализе поведения вектора кинетического момента динамически симметричного ротора, будут справедливы и при вращении ротора с произвольным эллипсоидом инерции.

Как и в главе 2, остановимся на рассмотрении системы регулирования на постоянном токе. Подставляя (2.81) с учетом (3.24) и (2.83) в (2.79) можно найти проекции моментов сил на неподвижные оси ξ_i, действующих на ротор со стороны электростатического поля.

Числовой пример 3.3. Рассмотрим электростатический гироскоп, у которого физические и геометрические характеристики описаны в примере 3.1. Опорные напряжения, подаваемые на электроды, относительной зазор между ротором и электродов такие же как в примере 2.3. Пусть вектор кинетического момента лежит в плоскости ξ₁ ξ₃. По формуле (2.60) получаем М_max=3.66*10^-4 г см²/с². Это значение достигается, когда 𝓀²=0.5 и когда вектор кинетического момента образует с осью ξ₃ угол π/4 или 3π/4, т.е. γ₁ γ₃ =0.5. По формуле М_max/L получаем величину возможного ухода электростатического гироскопа ω^*=4*10^-2 град/час.

Дата добавления: 2015-06-04