Метод зон Френеля

Френель показал, в случаях, отличающихся симметрией, нахождение амплитуды резуль­тирующего колебания может быть осуществлено простым алгебраическим или геометрическим суммированием.

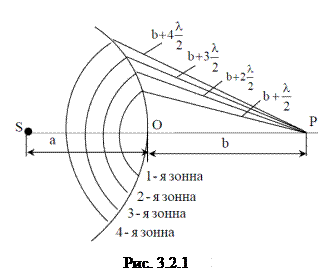Чтобы понять суть метода, разработанного Френелем, опреде­лим амплитуду светового колебания, возбуждаемого в точке Р сфе­рической волной, распространяющейся в изотропной однородной среде из точечного источника S (рис. 3.2.1). Волновые поверхности такой волны симметричны относительно прямой SP. Воспользовав­шись этим, разобьем изображенную на рисунке волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки Р отличается на l/2 (l - длина волны в той среде, в которой распространяется волна). Обладающие таким свойством зоны носят название зон Френеля.

Из рис. 3.2.2 видно, что расстояние b_m от внешнего края m -й зоны до точки Р равно 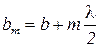(b — расстояние от вершины волновой поверхности О до точки Р). Колебания, приходящие в точку Р от аналогичных точек двух соседних зон (т. е. от точек, лежащих в середине зон или у внешних краев зон и т. д.), находятся в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на p.

Вычислим площади зон. Внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высоты h_m (рис. 3.2.2). Обозначим площадь этого сегмента через S_m. Тогда площадь m -й зоны можно представить в виде , где S_m-1 — площадь сферического сегмента, выделяемого внешней границей (m - 1) -й зоны.

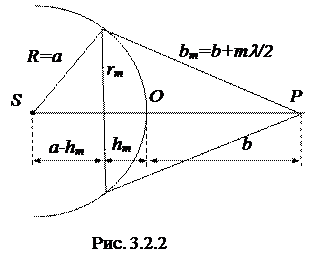Из рис. 3.2.2 видно, что

, (3.2.1)

где а - радиус волновой поверхности, r_m - радиус внешней границы m -й зоны.

Возведя скобки в квадрат, получим

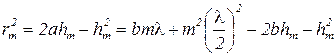, (3.2.2)

Отсюда

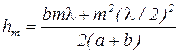. (3.2.3)

Ограничившись рассмотрением не слишком больших т, можно ввиду малости l пренебречь слагаемым, содержащим l². В этом приближении

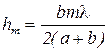(3.2.4).

Площадь сферического сегмента равна S=2pRh (R — радиус сферы, h - высота сегмента). Следовательно,

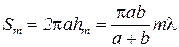, (3.2.5)

а площадь m-й зоны

. (3.2.6)

Полученное нами выражение не зависит от т. Это означает, что при не слишком больших т площади зон Френеля примерно одинаковы.

Из равенства (3.2.2) можно найти радиусы зон. При не слишком больших т высота сегмента h_m<a, поэтому можно считать, что 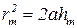. Подставив значение (3.2.4) для h_m, получим для радиуса внешней границы т-й зоны выражение

. (3.2.7)

Итак, плошади зон Френеля примерно одинаковы. Расстояние b_m от зоны до точки Р медленно растет с номером зоны т. Угол j между нормалью к элементам зоны и направлением на точку Р. также растет с т. Всe это приводит к тому, что амплитуда A_m колебания, возбуждаемого m -й зоной в точке Р, монотонно убыва­ет с ростом т. Даже при очень больших m, когда площадь зоны на­чинает заметно расти с т (см. (3)) А_m продолжает убывать. Таким образом, амплитуды колебании, возбуждаемых в точке Р зонами Френеля, образуют монотонно убывающую последовательность:

Фазы колебаний, возбуждаемых соседними зонами, отличаются на p. Поэтому амплитуда A результирующего колебания в точке Р может быть представлена в виде

(3.2.8)

В это выражение все амплитуды от нечетных зон входят с одним знаком, а от четных зон — с другим. Запишем выражение (3.2.8) в виде

(3.2.9)

Вследствие монотонного убывания A_m можно приближенно счи­тать, что

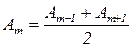. (3.2.10)

Тогда выражения в скобках будут равны нулю, и формула (3.2.9) упрощается следующим образом:

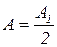. (3.2.11)

Согласно формуле (3.2.11) амплитуда, создаваемая в некоторой точке Р всей сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной.

Если на пути волны поставить непрозрачный экран с отверстием, оставляю­щим открытой только центральную зону Френеля, амплитуда в точке Р будет равна А₁, т. е. в два раза превзойдет амплитуду (3.2.11). Соответственно интенсивность света в точке Р будет в этом случае в четыре раза больше, чем в отсутствие преград между точками S и Р.

Колебания от четных и нечетных зон Френеля находятся в противофазе и, следовательно, взаимно ослабляют друг друга. Если поставить на пути световой волны пластинку, которая перекрывала бы все четные или нечетные зоны, то интенсивность света в точке Р резко возрастает. Такая пластинка, называемая зонной, действует подобно собирающей линзе. Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на p. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным или нечетным зонам, отличается на надлежащим образом подобранную величину. Такая пластинка называется фазовой зонной пластинкой. По сравнению с перекрывающей зоны амплитудной зонной пластинкой фазовая дает дополнительное увеличение амплитуды в два раза, а интенсивности света - в четыре раза.

Дата добавления: 2015-06-04