Расчета стержней 2 страница

[v] = 0.002l.

Решение.

Запишем уравнения прогибов, углов поворота, изгибающего момента и поперечных сил:

V (z) = A+Bz+Cz²/2+Dz³/6│₁+P (z-l)³/6EI_x+q (z-l)⁴/24EI_x│₂

φ (z) = - B – Cz - Dz²/2│₁ - P (z-l)²/2EI_x – q (z-l)³/6EI_x │₂

M_x (z) = -CEI_x - DzEI_x│₁ - P (z-l) - q (z-l)²/2│₂

Q_y (z) = -DEI_x│₁ – P - q (z-l) │₂

В соответствии с условиями закрепления стержня запишем граничные условия в следующем виде: V (0) = 0 → A = 0,

M_x (0) = - L → C = L/EI_x,

V (3l) = 0,

M_x (3l) = 0.

16,11

21,67

Рис.7

Для нахождения неизвестных B и D составим систему уравнений, учитывая граничные условия: V (3l) = 0 и M_x (3l) = 0. Решив эту систему, получим: D = -21.67/EI_x и B = 16.11/EI_x, откуда следует, что Q_y (0) = 21.67кН и φ (0) = -16,11/EI_x.

Теперь, учитывая найденные константы, уравнения интегральных характеристик можно переписать в следующем виде:

Q_y (z) = 21.67│₁ – P – q (z-l) │₂

M_x (z) = -L – 21.67z│₁ – P (z-l) – q (z-l)²/2│₂

φ (z) = -16.11/EI_x – Lz/EI_x + 21.67z²/2EI_x│₁ – P (z-l)²/2EI_x – q (z-l)³/6EI_x│₂

V (z) = 16.11z/EI_x + Lz²/2EI_x – 21.67z³/6EI_x│₁ + P (z-l)³/6EI_x + q (z-l)⁴/24EI_x│₂

Построение графиков будем производить аналогично примеру 1.

1 участок: 0 ≤ z ≤ l

Q_y (0) = 21.67 кН φ (0) = -16.11/EI_x

Q_y (l) = 21.67 кН φ (l) = -10.28/EI_x

M_x (0) = -5 кНм V (0) = 0

M_x (l) = 16.67 кНм V (l) = 15/EI_x

2 участок: l ≤ z ≤ 2l

Q_y (l) = 11.67 кН φ (l) = -10.28/EI_x

Q_y (2l) = -28.33 кН φ (2l) = 19.74/EI_x

M_x (l) = 16.67 кНм V (l) = 15/EI_x

M_x (2l) = 0 кНм V (l) = 0

Определим координаты экстремумов и значения функций в экстремальных точках:

1) Q_y (z1) = 21.67 – P – q (z1-l) = 0 → z1 = 1.58 м.

M_x (1.58) = -L + 21.67·1.58 – P (1.58-l) – q (1.58-l)²/2 = 20.07 кНм.

2) M_x (z2) = -L – 21.67·z2 = 0 → z2 = 0.23 м.

φ (0.23) = -16.11/EI_x – L·0.23/EI_x + 21.67(0.23)²/2EI_x = -16.69/EI_x.

3) φ (z3) = -16.11/EI_x – L·z3/EI_x + 21.67(z3)²/2EI_x – P (z3-l)²/2EI_x –

- q (z3-l)³/6EI_x = 0 → z3 = 1.47м.

V (1,47) = 16.11·1,47/EI_x + L·(1,47)²/2EI_x – 21.67·(1,47)³/6EI_x +

+ P (1,47-l)³/6EI_x + q (1,47-l)⁴/24EI_x = 17,61/EI_x.

Расчет на прочность: σ_max ≤ [σ], σ_max = M_{x max}/I_x.

Для прямоугольника I_x = bh³/12 = b (1.5b)³/12 = 0.28b⁴.

Найдем b: b = 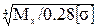= = 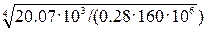0.145м.

h = 0.218м.

Расчет на жесткость: V_max ≤ [v].

17.61/EI_x = 0.002 → I_x = 17.61·10³/ (2·10¹¹·0.002) = 0.000044 м⁴.

I_x = 0.28b⁴ → b = 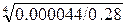= 0.112 м, h = 0.168 м.

Из полученной пары значений необходимо выбрать удовлетворяющие условиям прочности и жесткости. После выбора из стандартного ряда: b = 0.15м, h = 0.22м

.

Пример 4.

Для заданной схемы нагружения стержня построить графики поперечных сил, изгибающего момента, угловых и линейных перемещений. Из расчета на прочность и жесткость подобрать размеры двутаврового поперечного сечения при следующих исходных данных: L = 20 кНм, q = 10 кН/м, l = 1м, [σ] = 160 МПа, [V] = 0.002l.

Решение.

Заменим промежуточную опору эквивалентной ей неизвестной пока реакцией R (см. рис.), которая будет внесена в уравнения как сосредоточенная сила:

V (z) = A+Bz+Cz²/2+Dz³/6 + q z⁴/24EI_x │₁+R (z-l)³/6EI_x│₂

φ (z) = - B – Cz - Dz²/2 - q z³/6EI_x │₁ - R (z-l)²/2EI_x │₂

M_x (z) = -CEI_x - DzEI_x q z³/6EI_{x 1} - R (z-l) │₂

Q_y (z) = -DEI_x - q z │₁ – R │₂

Запишем граничные условия: V (0) = 0 → A = 0,

M_x (0) = 0 → С = 0,

V (l) = 0 V (3l) = 0 M_x (3l) = -L → V'' (3l) = L/EI_x

Составив систему из трех неиспользованных граничных условий, найдем неизвестные B, R и D: D = -7.94/EI_x → Q_y (0) = 7.94 кН,

B = 0.91/EI_x→ φ (0) = -0.91/EI_x,

R = 0.6 кН.

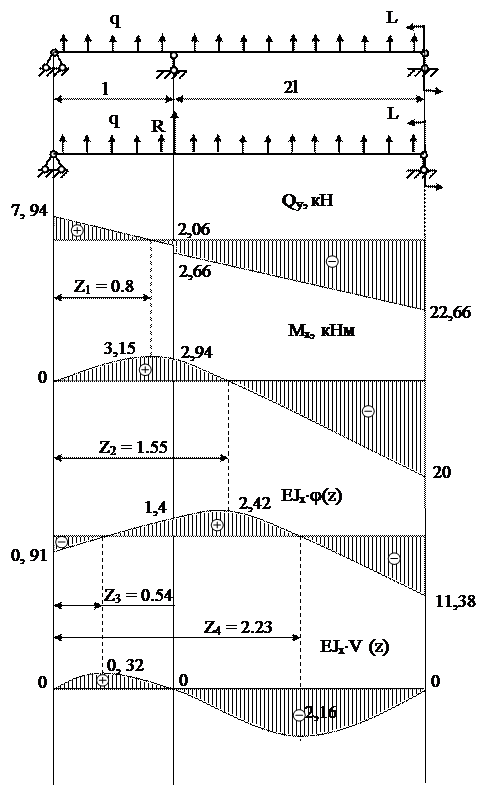
Рис.8

С учетом найденных констант уравнения перепишутся следующим образом:

V (z) = 0.91z/EI_x - 7.94 z³/6EI_x + q z⁴/24EI_x │₁+0.6 (z-l)³/6EI_x│₂

φ (z) = -0.91/EI_x + 7.94 z²/2EI_x - q z³/6EI_x │₁ – 0.6 (z-l)²/2EI_x │₂

M_x (z) = 7.94z - q z³/6EI_x│₁ - 0.6 (z-l) │₂

Q_y (z) = 7.94 - q z │₁ – 0.6│₂.

Вычислим значения для границ участков:

1 участок: 0 ≤ z ≤ l

Q_y (0) = 7.94 кН φ (0) = - 0.91/EI_x

Q_y (l) = - 2.06 кН φ (l) = 1.4/EI_x

M_x (0) = 0 кНм V (0) = 0

M_x (l) = 2.94 кНм V (l) = 0

2 участок: l ≤ z ≤ 3l

Q_y (l) = - 2.66 кН φ (l) = 1.4/EI_x

Q_y (3l) = - 22.66 кН φ (3l) = -11.38/EI_x

M_x (l) = 2.94 кНм V (l) = 0

M_x (3l) = - 20 кНм V (l) = 0

Расчет координат экстремума и значений интегральных характеристик в экстремальных точках проведем аналогично показанным ранее примерам. В нашем случае: z₁ = 0.8 м, M_x (0,8) = 3,15 кНм,

z₂ = 1.55 м, φ (1.55) = 2.42/EI_x,

z₃ = 0.54 м, V (0.54) = 0.32/EI_x,

z₄ = 2.23 м, V (2.23) = - 2.16/EI_x.

По полученным значениям строим графики.

Расчет на прочность и жесткость:

1) Расчет на прочность: σ_max ≤ [σ].

σ_max = M_{x max}/ W_x.

В пределе получим: M_{x max}/ W_x = [σ].

Откуда: W_x = M_{x max}/[σ] = 20·10³/160·10⁶ = 0,000125 м³ = 125 см³.

Из таблиц сортамента выберем двутавр № 18 с W_x = 143 см³.

2) Расчет на жесткость: V_max ≤ [V].

2.16/EI_x = 0.002·1,

откуда: I_x = 2.16·10³/(0.002·2·10¹¹) = 0.0000054 м⁴ = 540 м⁴.

Из таблиц сортамента выберем двутавр № 14 с I_x = 572 см⁴.

Окончательно примем двутавр № 18, т.к. он удовлетворяет условиям прочности и жесткости.

Пример 5.

Для заданной схемы нагружения кривого стержня радиуса R построить эпюры продольных и поперечных сил, а также изгибающего момента при следующих исходных данных: L = 10 кНм, l = 1 м.

Рис.9

Решение.

Х

Данный кривой стержень является статически неопределимым, т.к. имеет четыре связи – три в жесткой заделке и одну – в подвижном шарнире. Задачу будем решать методом сил, т.е. «лишнюю» связь отбрасываем и заменяем ее реакцией.

Рис.10

Запишем каноническое уравнение метода сил:

х·δ₁₁ + δ_1Р = 0,

где х – неизвестная реакция, заменяющая отброшенную связь,

δ₁₁ – перемещение точки А от силы х = 1,

δ_1Р – перемещение точки А под действием внешних сил.

Перемещения будем искать при помощи интеграла Мора.

Составим уравнения моментов:

- от действия внешних сил M_xp(φ) = 0│₁ - L│₂;

- от действия силы х = 1: M_x1(φ) = - 1Rsin φ.

δ₁₁ = 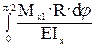= = 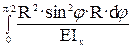= 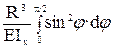0.785/EI_x

δ_1Р = 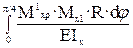+ 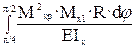= 7.07/EI_x.

Определим неизвестную реакцию:

х = - δ_1Р/ δ₁₁ = - 7,07· EI_x/ EI_x·0.785 = - 9 кН.

Теперь рассмотрим стержень, приложив в подвижном шарнире найденную реакцию х. Составим уравнения изгибающих моментов, поперечных и продольных сил:

M_x(φ) = X·R·sin φ│₁ - L│₂,

Q_y (φ) = X·cos φ│_{1, 2}

N (φ) = - X·sin φ│_{1, 2}

Рассчитаем значения функций на границах участков.

1 участок - 0 ≤ φ ≤ π/4: 2 участок - π/4 ≤ φ ≤ π/2:

N (0) = 0 N (π/4) = -6.36 кН

N (π/4) = -6.36 кН N (π/2) = -9 кН

Q_y (0) = 9 кН Q_y (π/4) = 6.36 кН

Q_y (π/4) = 6.36 кН Q_y (π/2) = 0

M_x(0) = 0 M_x(π/4) = -3.64кНм

M_x(π/4) = 6.36 кНм M_x(π/2) = -1 кНм

Построим графики:

Рис.11

Пример 6.

Для кривого стержня радиуса r, показанного на рисунке, построить эпюры продольных и поперечных сил, а также изгибающего момента при следующих исходных данных: r = 1м, Р = 10 кН, [σ] = 160 МПа. Найти также перемещение точки А.

Рис.12

Решение.

Данный стержень является статически определимым, поэтому решать задачу будем классическим методом.

Рис.13

Реакции в опорах найдем, составив уравнения равновесия:

Σ Y = R₁ + R₃ + P₁·cos45 = 0,

Σ X = R₂ + P₁·sin45 = 0,

Σ M_B = R₁·r + P·r·sin45 = 0.

Решая систему, получим:

R₂ = -P·sin45 = -7.07кН,

R₁ = -P·r·sin45/r = -7.07кН,

R₃ = - P·cos45 - R₁ = 0.

Составим теперь уравнения продольных, поперечных сил и изгибающего момента:

M_x (φ) = - R₁·r·sinφ│₁ – P·r(φ – π/4) │₂,

Q_y (φ) = - R₁·cosφ│₁ – P·cos(φ – π/4) │₂,

N (φ) = R₁·sinφ│₁ + P(φ – π/4) │₂.

Рассчитаем значения функций на границах участков.

1 участок - 0 ≤ φ ≤ π/4: 2 участок - π/4 ≤ φ ≤ π/2:

N (0) = 0 N (π/4) = -5 кН

N (π/4) = -5 кН N (π/2) = 0 кН

Q_y (0) = 7.07 кН Q_y (π/4) = -5 кН

Q_y (π/4) = 5 кН Q_y (π/2) = -7.07 кН

M_x(0) = 0 M_x(π/4) = 5 кНм

M_x(π/4) = 5 кНм M_x(π/2) = 0 кНм

7.07

Построим графики:

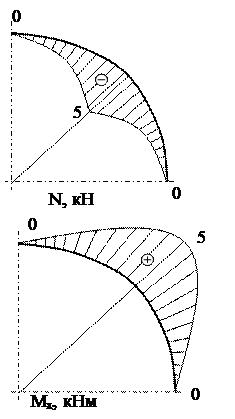Рис.14

Расчет на прочность произведем по изгибающему моменту:

σ_max = M_{x max}/ W_x ≤ [σ],

где W_x – момент сопротивления сечения изгибу.

W_x = M_{x max}/ [σ] = 5·10³/ 160·10⁶ = 3.125·10^-5 м³.

С другой стороны, W_x = 0.1d³.

Приравняв полученные выражения, найдем:

d = = = 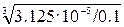0.068 м.

Из стандартного ряда примем d = 0.07 м.

Найдем линейное перемещение точки А. Для этого, в точке А приложим единичную силу в направлении предполагаемого перемещения.

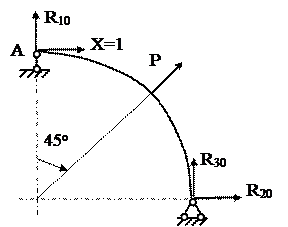Рис.15

Для определения реакций в опорах составим следующие уравнения равновесия:

Σ Y = R₁₀ + R₃₀ = 0,

Σ X = Х + R₂₀ = 0,

Σ M_B = X·r + R₁₀·r = 0.

Решая систему, получим:

R₁₀ = - X·r/r = - 1,

R₃₀ = - R₁₀ = 1,

R₂₀ = - X = -1.

Запишем уравнение изгибающего момента:

M_x0 (φ) = - R₁₀·r·sin φ – X·r (1 - cos φ).

Перемещение точки А найдем с помощью интеграла Мора:

δ_А = = +

+ = =

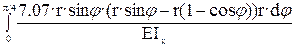= = 0,008м.

Пример 7.

Для стержневой системы, показанной на рисунке, построить графики поперечных сил и изгибающего момента, из расчета на прочность подобрать размеры квадратного поперечного сечения при следующих исходных данных: q = 10 кН/м, L = 20 кНм, l = 1 м, [σ] = 160 МПа. Найти перемещение

сечения А.

Рис.16

Решение.

Рассматриваемая стержневая система является статически определимой, т.к. не имеет «лишних» связей, поэтому решать ее будем классическим методом, т.е., разбив систему на два стержня, запишем уравнения интегральных характеристик для каждого в отдельности.

Для первого стержня:

Q_y1 (z) = Q_y1 (0) + qz,

M_x1(z) = M_x1(0) + Q_y1 (0)·z + qz²/2.

Для второго стержня:

Q_y2 (z) = Q_y2 (0),

M_x2 (z) = M_x2 (0) + Q_y2 (0)·z.

Запишем граничные условия: M_x1 (0) = 0,

M_x2 (l) = L,

Q_y2 (l) = 0,

M_x1(l) = M_x2 (0) – условие сопряжения.

Используя граничные условия и условие сопряжения, определим неизвестную константу Q_y1 (0): Q_y1 (0) = 15 кН.

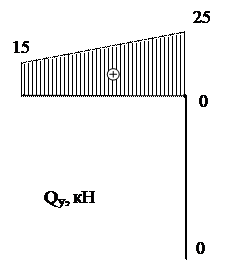
Построим графики.

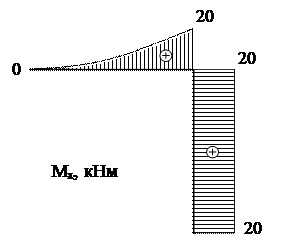Рис.17

Расчет на прочность.

Условие прочности: σ_max ≤ [σ].

В нашем случае σ_max = M_{x max} / W_x; W_x = a³/6.

6M_{x max}/ a³ = [σ] → a = 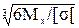= = 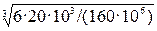0.028 м.

Примем а = 0.03 м.

Пример 8.

Для стержневой системы, показанной на рисунке, построить эпюры поперечных сил и изгибающего момента при следующих исходных данных:

q = 10 кН, l = 1м.

Рис.18

Решение.

Данная система является статически неопределимой, поэтому сначала необходимо определить количество «лишних» связей: n = m – 3,

где m – количество связей, наложенных на систему.

В нашем случае: n = 5 – 3 = 2, т.е. система дважды статически неопределима.

Для решения задачи отбросим «лишние» связи в неподвижном шарнире и заменим их неизвестными пока реакциями Х₁, Х₂.

основная система метода сил

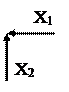Рис.19

Запишем каноническую систему уравнений метода сил:

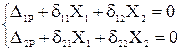
Здесь Х₁, Х₂ – силы, действующие как реакции в опоре,

Δ_1Р, Δ_2Р – перемещения опорных сечений, вызванные внешними нагрузками в основной системе,

δ₁₁, δ₂₂, δ₁₂, δ₂₁ – перемещения от единичных сил (причем δ₁₂ = δ₂₁).

Рассмотрим основную систему:

а) нагруженную реальной нагрузкой (без реакций опор)

1 стержень: 2 стержень:

Q_y1 (0) = 0 Q_y2 (0) = 0

M_x1 (0) = 0 M_x2 (0) = 0

M_x1 (z) = 0 M_x2 (z) = qz²/2

б) нагруженную единичной горизонтальной силой

1 стержень: 2 стержень:

M⁰_x1 (0) = 0 M⁰_x2 (0) = M⁰_x1 (l) = -1·l

Q⁰_y1 (0) = -1 Q⁰_y2 (0) = 0

M⁰_x1 (z) = Q⁰_y1 (0)·z = -1z M⁰_x2 (z) = -1·l

в) нагруженную единичной вертикальной силой

1 стержень: 2 стержень:

M⁰_x1 (0) = 0 M⁰_x2 (0) = 0

Q⁰_y1 (0) = 0 Q⁰_y2 (0) = -1

M⁰_x1 (z) = 0 M⁰_x2 (z) = Q⁰_y2 (0) ·z = -1·z

Определим перемещения:

Δ_1Р = = =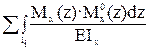

Δ_2Р = =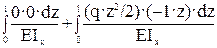

δ₁₁ = =

δ₂₂ =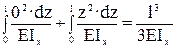

δ₁₂ =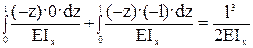

С учетом найденных значений перемещений перепишем каноническую систему уравнений метода сил следующим образом:

Решая систему, получим: Х₁ = 3ql / 7

Х₂ = -ql / 28.

Отрицательное значение реакции Х₂ говорит о том, что направление этой реакции на схеме необходимо изменить на противоположное.

Теперь, когда известны все силы, можно строить графики ИХНС.

Запишем уравнения поперечных сил и изгибающего момента для каждого стержня в отдельности.

1 стержень:

Q_y1 (z) = Q_y1 (0) = X₁ = ql / 28.

M_x1 (z) = M_x1 (0) + Q_y1 (0)·z = ql·z / 28.

2 стержень:

Q_y2 (z) = Q_y2 (0) + q·z = -3ql / 7 + q·z.

M_x2 (z) = M_x2 (0) + Q_y2 (0)·z + qz² / 2 = ql² / 28 – 3ql·z / 7 + q·z² / 2.

M_x2 (0) = M_x1 (l) = ql² / 28.

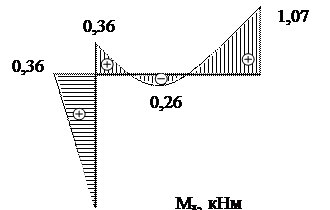Рис.20

Пример 9.

Для заданной схемы нагружения стержня определить значение критической силы.

Решение.

Рис.21

Форму изогнутой оси выберем в тригонометрическом виде (см. приложение 2):

V (z) = a (1 – cosπz/l).

Для расчетов и проверки граничных условий нам потребуется первая, вторая и третья производные: V' (z) = aπ/l·sinπz/l,

V'' (z) = aπ²/l²· cosπz/l,

V''' (z) = -aπ³/l³· sinπz/l.

Граничные условия на концах стержня: V (0) = 0,

V' (0) = 0,

V' (l) = 0,

V''' (l) = 0.

Запишем уравнение равновесия деформированного стержня:

EI_{x 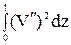= q .}

EI_x = EI_xa²π⁴/l⁴· (z/2 + l/4π·sin2πz/l) │ 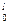= EI_x·a²π4/2l³.

q = (qa²π²/l²) · (z²/4 + l²/8π²·cos2πz/l) │ 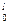= qa²π²/4.

Приравняем полученные выше выражения:

EI_x· a²2π⁴/2l³ = qa²π²/4.

Формула Эйлера для критической силы записывается в виде: P_кр = EI_xπ²/(μl)².

Приведем полученное выражение к виду формулы Эйлера:

(ql)_кр = EI_x π²/ (0.71·l)².

Пример 10.

Груз массой 400 кг падает с высоты Н на балку двутаврового сечения № 20, длина балки l =2м, I_x = 2370 см⁴, W_x = 237 см³. Определить максимальные напряжения, возникающие в балке при ударе и высоту падения груза при [σ] = 160 МПа.

Дата добавления: 2015-06-04