Возможности автоматов

Конечные автоматы позволяют избежать использования в программах, реализующих алгоритмы, условного оператора «if», а также операторов выбора (например, «case»). Поэтому «автоматный» стиль программирования предпочтителен при построении сложных программ. Рассмотрим несколько примеров, демонстрирующих преимущества использования автоматов в процессе решения некоторых задач.

Счетчик. Требуется создать устройство, которое на каждом такте выдает целое число, большее предыдущего на единицу; при достижении некоторого предельного значения серия выводимых значений повторяется. Пусть предельное значение равно шести. Автомат, реализующий алгоритм, является автоматом Мура и может быть описан в стандартном виде:

	1/0	2/1	3/2	4/3	5/4	6/5	0/6

Предположим, что вслед за этим счетчиком предполагается разместить еще один, который бы отсчитывал количество шестерок. В таком случае достаточно в качестве выходного алфавита принять следующий набор: 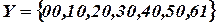. Первая из цифр выводится на экран, вторая подается на выход, являющийся входом для следующего счетчика. Если на вход второго счетчика подается 0, то его состояние не меняется и на выход подается пустой символ. Если же подается единица, то он изменяет состояние так же, как и рассмотренный выше счетчик:

	0/-	0/-	0/-	0/-	0/-	0/-
	1/0	2/1	3/2	4/3	5/4	0/5

Однако следует отметить, что счетчики рассмотренного типа не позволяют считать до бесконечности. Это ограничение принципиально для конечных автоматов. Однако данной схемы достаточно для реализации обычных электронных часов [1].

Счетчик является примером так называемых автономных автоматов, входной алфавит которых содержит единственный символ. Если считать, что в каждой вершине графа имеется один выход, причем выходной сигнал совпадает с номером состояния, то он является эквивалентом отношения порядка, а граф автономного автомата – это простой ориентированный граф [2, 3]. Для входного слова достаточной длины выходное слово автономного автомата содержит периодически повторяющееся подслово.

Проверка четности. Пусть входной алфавит содержит два символа – ноль и единицу. Требуется построить алгоритм, согласно которому на выходе повторяется входное слово, но после каждого подслова, содержащего три символа, должен быть вставлен символ «0», если количество единиц в подслове четно, и символ «1» в противном случае.

Прежде всего отметим, что выходной алфавит конструируемого автомата не может состоять только из нуля и единицы, так как количество символов во входном и выходном словах должно быть одно и то же (требование автоматности).

Это требование удовлетворяется введением такого выходного алфавита: 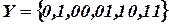. Выход после третьего символа состоит из двойки символов: «00», «01», «10», «11». Обозначим состояния автомата как «-», «0», «1», «00», «01», «10», «11», подразумевая под «-» стартовое состояние. После этого оказывается возможным построение автомата проверки четности в следующем виде:

	-
	0/0	00/0	10/0	-/00	-/01	-/01	-/00
	1/1	01/1	11/1	-/11	-/10	-/10	-/11

Выполним кодирование состояний и выходов, сопоставляя состояние «-» и номер 0, «0» – номер 1, «1» – 2, «00» – 3, «01» – 4, «10» – 5, «11» – 6; выход «0» и номер элемента алфавита 0, выход «1» и номер 1, «00» – 2, «01» – 3, «10» – 4, «11» – 5. Тогда таблица построенного автомата примет такой вид:

	1/0	3/0	5/0	0/2	0/3	0/3	0/2
	2/1	4/1	6/1	0/5	0/4	0/4	0/5

Граф этого автомата изображен на рис. 4.7.

Отметим, что состояния 3 и 6 эквивалентны. Это же относится и к паре состояний 4 и 5. Поэтому в данном случае имеется возможность минимизировать найденный автомат, объединив состояния 3, 6 в класс 3 эквивалентных состояний, а классы 4, 5 – в класс 4. Минимизированный автомат, эквивалентный исходному, в таком случае можно изобразить графически (рис. 4.8) и в виде таблицы:

	1/0	3/0	4/0	0/2	0/3
	2/1	4/1	3/1	0/5	0/4

Если поставлена задача проверить четность в словах длиной n, то граф неминимизированного автомата будет содержать 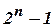вершин, а минимизированного – .

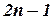Таким образом, задача минимизации, т.е. построение автомата, эквивалентного исходному, но с меньшим количеством состояний, является очень важной.

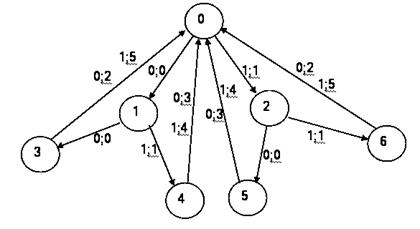
Рис. 4.7. Граф автомата проверки четности

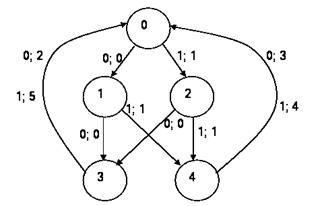
Рис. 4.8. Минимизированный автомат проверки четности

Сумматор. Пусть поставлена задача найти сумму двух чисел в троичной системе счисления. Сложение будем производить поразрядно с учетом возможного перенесения в старший разряд.

Напрямую автомат построить в этом случае невозможно, поэтому требуется ввести в рассмотрение входной алфавит, состоящий из пар цифр.

Учитывая, что слагаемые можно переставлять, кодировщик представим в виде матрицы X:

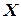
	0 (0+0)	1 (0+1)	2 (0+2)
	1 (1+0)	2 (1+1)	3 (1+2)
	2 (2+0)	3 (2+1)	4 (2+2)

Например, пара цифр (1,2) кодируется как элемент X[1,2] = 3, как и пара цифр (2,1). Автомат суммирования может быть задан в виде матрицы :

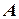
	0/0 (0+0 = 0·3 + 0)	0/1 (0+1= 0·3 + 1)
	0/1 (1+0 = 0·3 + 1)	0/2 (1+1= 0·3 + 2)
	0/2 (2+0 = 0·3 + 2)	1/0 (2+1= 1·3 + 0)
	1/0 (3+0 = 1·3 + 0)	1/1 (3+1= 1·3 + 1)
	1/1 (4+0 = 1·3 + 1)	1/2 (4+1= 1·3 + 2)

Собственно, сложение производится поразрядным (начиная с младшего разряда) пропусканием двух слов a и b (т.е. чисел, представленных в троичной системе счисления) через цепочку (рис. 4.9).

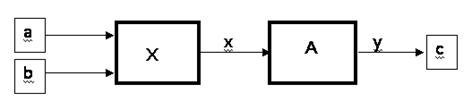
Рис. 4.9. Автоматное суммирование

Достоинством автоматного суммирования является то, что все действия ограничиваются нахождением элементов матриц X и А.

Автоматное декодирование. Рассмотрим основную идею на примере. Пусть задана таблица кодов, получаемых как пути в дереве (рис. 4.10). С движением от узла влево сопоставим символ «а», прямо – «б», вправо – «в». Таблица кодов имеет следующий вид:

Р	а	Т	ва	Л	бба
К	ба	Ы	ббб	С	вб
О	бв	У	вв	М	ббв

В качестве номеров состояний автомата примем номера узлов, не являющихся листами; корень дерева имеет номер 0.

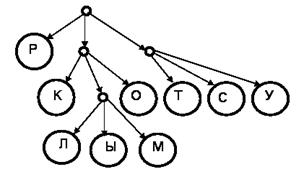
Рис. 4.10. Дерево кодирования

Выходной алфавит содержит буквы, соответствующие листам, а также пустой символ «-». В результате получаем таблицу автомата следующего вида:

а	0/Р	0/К	0/Т	0/Л
б	1/-	3/-	0/С	0/Ы
в	2/-	0/О	0/У	0/М

Для проверки работоспособности построенного автомата предлагается самостоятельно получить выходное слово, если на вход подается слово «бабвабвббвбббвбббабв». Входное слово следует подавать в порядке слева направо (первый входной символ – б, второй – а, третий – б и т.д.).

По каждой из рассмотренных задач желательно самостоятельно сконструировать автоматы, реализующие различные частные случаи.

С помощью конечных автоматов решается огромное количество задач. Тем не менее, имеется множество задач, для которых не существует алгоритмического решения и, следовательно, нельзя построить автомат.

Краткий перечень задач, для которых отсутствует алгоритм решения, таков [1]:

1. Проблема остановки. По описанию произвольного алгоритма и его исходных данных определить, остановится ли алгоритм на этих данных или будет работать вечно.

2. Проблема эквивалентности алгоритма. По двум произвольным алгоритмам определить, будут ли они выдавать одинаковые выходные результаты при одинаковых входных данных.

3. Проблема эквивалентности грамматики. По двум произвольным грамматикам установить, совпадают ли порожденные ими языки.

4. Проблема тотальности. По произвольному заданному алгоритму определить, будет ли он завершаться во всех возможных наборах.

Дата добавления: 2015-06-04