Вычислимость по Тьюрингу

Алану Тьюрингу принадлежит идея построения гипотетической вычислительной машины. Опишем основные положения формальной теории машины Тьюринга.

Считаются заданными:

1. Внешний алфавит .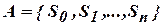

2. Внутренний алфавит .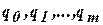

3. Внешняя память – лента с ячейками. В каждой из ячеек может находиться тот или иной символ внешнего алфавита. Таким образом, лента содержит слова – набор символов, помещенных в ячейку.

4. Управляющая головка. На каждом такте управляющая головка находится напротив некоторой ячейки.

Работа машины Тьюринга описывается набором команд, имеющих синтаксис

,

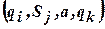где 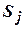– содержимое ячейки, напротив которой находится управляющая головка; 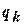– новое внутреннее состояние машины; 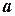– ячейка, которая может содержать символ из внешнего алфавита.

Результат работы команд: при наличии в структуре 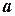символа 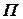головка сдвигается вправо к следующей ячейке; при наличии символа 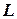происходит сдвиг влево; если в структуре 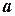присутствует символ внешнего алфавита, то в рассматриваемую ячейку заносится этот символ, а старый убирается.

Гипотетическая машина Поста строится сходным образом.

Команды теории Поста называются приказами. Считаются заданными (выполнимыми) шесть приказов:

1. Записать 1 и перейти к приказу .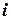

2. Записать 0 и перейти к приказу .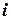

3. Сдвинуть вправо и перейти к приказу .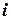

4. Сдвинуть влево и перейти к приказу .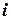

5. Если в ячейке 1, то перейти к приказу .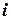

6. Если в ячейке 0, то перейти к приказу .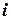

Более детальное рассмотрение показывает, что машины Тьюринга и Поста эквивалентны.

Набор команд для преобразования слова называется Т-программой. Т-программа может быть задана двумя способами: табличным способом, который сводится к заполнению таблицы

	Внешний алфавит
Внутренний алфавит

и в виде потока команд.

Пример 1. Рассмотрим работу машины Тьюринга, заданную следующей таблицей:

	-
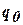
	П	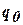П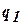
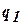
	1П	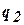П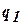

Последовательность действий:

-	-				-	-	-

-	-				-	-	-

-	-				-	-	-

-	-				-	-	-

-	-					-	-

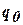
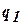
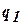
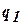
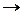
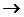
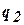
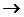
Для состояния 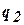описание отсутствует, т.е. при достижении состояния 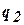работа машины Тьюринга завершается.

Итак, слово 111 преобразовалось в слово 1111. Это значит, что вычислимой по Тьюрингу является функция, прибавляющая к целому числу единицу.

Целью работы машины Тьюринга является преобразование некоторого исходного слова в заданное.

Пример 2. Построить Т-программу, с помощью которой слово «лето» преобразуется в слово «осень».

Внешний алфавит:

;

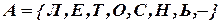-	Л	Е	Т	О	С	Н	Ь	-
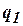
	ОП	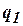СП	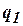ЕП	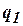				ЬП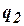

Синтез машины Тьюринга. Пусть надо решить несколько задач, для каждой из которых имеется Т-программа. Существует две возможности:

1) применить несколько машин Тьюринга (для каждой задачи);

2) оставаясь в рамках одной машины Тьюринга, записать входные слова в различных областях одной ленты; финальное состояние первой задачи отождествить со стартовым состоянием второй.

Универсальной машиной Тьюринга называется машина, реализующая все задачи в заданном алфавите. К. Шеннон поставил вопрос о сложности универсальной машины Тьюринга, определив сложность как произведение количеств внутренних и внешних состояний.

К настоящему времени установлено, что для построения универсальной машины Тьюринга достаточно располагать четырьмя внутренними и шестью внешними состояниями.

Дата добавления: 2015-06-04