Рекурсия

Понятие рекурсии связано с фамилиями таких ученых, как Клини и Черч. Клини ввел понятие частичной рекурсивной функции. Им высказана гипотеза: все частичные функции являются частично рекурсивными (эта гипотеза недоказуема).

В силу тезиса Черча вычислимость эквивалентна рекурсивности (этот тезис также недоказуем).

Формальная теория строится следующим образом. Функция является частично рекурсивной, если она за конечное число шагов может быть получена из простейших функций путем применения простейших операций.

Функция является общерекурсивной или рекурсивной, если она частично рекурсивна и всюду определена.

Три простейшие функции теории:

1) – функция, которая позволяет добавлять к аргументу единицу;

2) 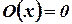– операция обнуления;

3) 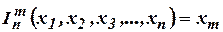– оператор проектирования (индекс показывает количество аргументов в функции, а 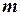– указывает,который из них предлагается выбрать, например, ).

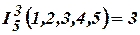Три простейшие операции теории:

1. Суперпозиция. Пусть заданы следующие функции:

,

,

,

.

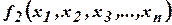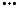
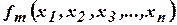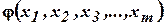Суперпозицией функции , построенной с помощью функции 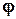, называется функция 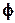от тех же аргументов 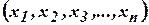, которая представляет собой следующее:

.

Пример 1. Заданы следующие функции:

;

;

;

.

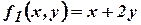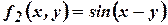Выполним суперпозицию:

.

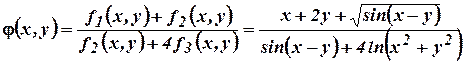Пример 2. Дана функция

.

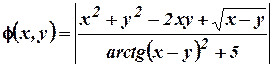Требуется представить ее в сокрашенном виде. Для этого введем отдельные функции:

.

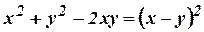Введем новое обозначение:

.

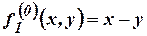Исходная функция приняла следующий вид:

.

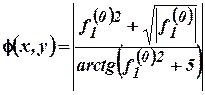Обозначим 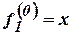, тогда

.

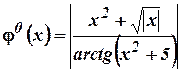Введем следующие обозначения:

.

Тогда

.

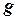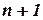2. Примитивная рекурсия. Пусть заданы следующие функции: – местная ; – местная 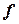; 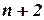– местная .

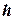Построение примитивной рекурсии:

,

.

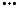
Замечание. В случае требуется некоторое уточнение:

;

…

.

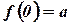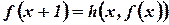Основная идея сводится к вычислению функции при значении аргумента на основании вычисления этой же функции при значении аргумента .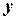

Основные функции являются рекурсивными.

Сложность состоит в подборе 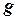и .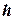

Пример. Доказать, что функция является примитивно-рекурсивной.

Пусть 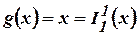, , 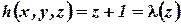, 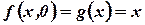тогда

;

;

.

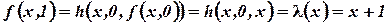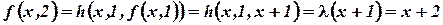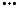
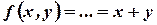Итак, функция 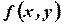является примитивно-рекурсивной.

Построим рекурсивную функцию с помощью следующей конструкции:

;

;

;

;

;

;

.

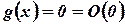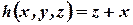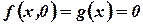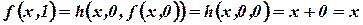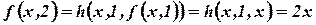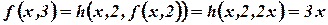3. -оператор. Рассмотрим функцию 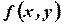. В некоторых случаях 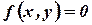. Корней 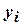может оказаться несколько. C помощью -оператора считается возможным реализовать следующую последовательность операций:

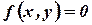– – находят все корни при заданном ;

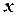– среди всех корней выбирают наименьший.

Дата добавления: 2015-06-04