Квантовые статистики Ферми-Дирака и Бозе-Эйнштейна

Для решения многих задач статистической физики достаточно знать функцию распределения системы по возможным состояниям. В классической стат. физике основными являются распределения Гиббса и распределения Максвелла по энергиям отдельных частиц. Распределение Гиббса обобщается на случаи квантовых систем введением минимального объема фазового пространства . Распределение же по энергиям будет зависеть от природы частиц, образующих систему.

а) Если частицы обладают целым спином, то они называются бозонами и подчиняются статистике Бозе-Эйнштейна с фукцией распределения

,

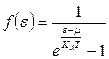где μ- химический потенциал.

Бозонами являются фотоны, фононы, К- и π-мезоны, ядра и атомы с целым спином. В этом случае справедлив принцип неразличимости частиц и в одном квантовом состоянии может находиться любое число частиц 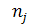= 0, 1, 2,…∞.

Полная энергия системы равна .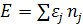

j- номер квантового состояния, - его энергия, 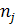- число частиц.

б) Если же частицы имеют полуцелый спин, то они называются фермионами и подчиняются статистике Ферми- Дирака с фукцией распределения

.

К ним относятся электроны, нейтроны, протоны, атомы и ядра с полуцелым спином. В этом случае кроме принципа неразличимости частиц работает принцип запрета Паули, то есть в каждом квантовом состоянии может находиться не более одной частицы

Ясно, что энергия такой системы 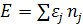будет отличаться от энергии системы бозонов.

2.20. Условие перехода к классической статистике. Критерий вырождения.

Рассмотрим квантовые распределения Ферми-Дирака и Бозе-Эйнштейна

.

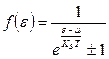Газы, подчиняющиеся квантовым статистикам принято называть вырожденными. При выполнении условия 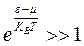различие между этими статистиками исчезает и

.

Это соотношение называют распределением Больцмана. По сути, оно совпадает с классическим распределением Максвелла-Больцмана. Газы, подчиняющиеся классической статистике, называют невырожденными.

При условием применимости классической статистики будет неравенство

.

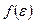Расстояние между энергетическими уровнями для поступательного движения малы по сравнению с , поэтому вместо удобно ввести среднее число частиц, энергии которых лежат от ε до ε+dε

,

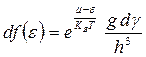где g=2I+1, - элемент объема 6-ти мерного фазового пространства для одной частицы (µ - пространства). подчиняется условию нормировки

,

которое выражает постоянство числа частиц в данном объеме. Пусть энергия частицы сводится к кинетической ,

тогда

Витоге критерий применимости классической статистики примет вид:

.

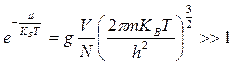При выполнении обратного условия

газ вырождается и для его описания следует применять квантовые статистики. Видно, что вырождение может быть вызвано следующими причинами: а) большая концентрация (), б) малая масса частиц, в) низкая температура, либо любым сочетанием этих факторов.

Дата добавления: 2015-06-04