Математическое моделирование

Основные понятия теории массового обслуживания. Графы состояний, уравнения Колмогорова, Эрланга. Типы задач машиностроения, решаемые с использованием теории массового обслуживания.

Задачи о движении снаряда

Разработкой математических моделей, получением число-вых результатов и анализом показателей эффективности занимается теория массового обслуживания (ТМО). Методы ТМО основаны на расчетах,

основанных на случайных процессах, в частности, на процессах

гибели и размножения.

Теория массового обслуживания занимается изучением процессов, связанных с массовым обслуживанием, разработкой методов решения типичных задач массового обслуживания.

Проводя рассуждения аналогичным образом для всех других состояний системы, получим систему дифференциальных уравнений, которые называются уравнениями А.Н. Колмогорова:

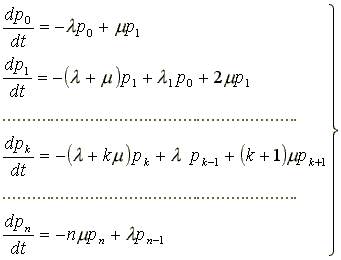
Для составления уравнений Колмогорова существуют общие правила.

Уравнения Колмогорова позволяют вычислить все вероятности состояний СМО Si в функции времени pi(t). В теории случайных процессов показано, что если число состояний системы конечно, а из каждого из них можно перейти в любое другое состояние, то существуют предельные (финальные) вероятности состояний, которые показывают на среднюю относительную величину времени пребывания системы, в этом состоянии. Если предельная вероятность состояния S0 - равна p0 = 0,2, то, следовательно, в среднем 20% времени, или 1/5 рабочего времени, система находится в состоянии So. Например, при отсутствии заявок на обслуживание к = 0, р0 = 0,2,; следовательно, в среднем 2 ч в день система находится в состоянии So и простаивает, если продолжительность рабочего дня составляет 10 ч.

Так называется широкий класс случайных процессов, происходящих в системе, размеченный граф состояний которой изображен на рис.

Граф состояний многоканальной СМО с отказами

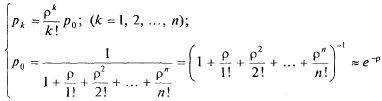
Формула Эрланга

Под системой массового обслуживания (СМО) будем понимать ком-плекс, состоящий: а) из случайного входящего потока требований (событий), нуждающихся в обслуживании; б) дисциплины очереди; в) механизма, осуще-ствляющего обслуживание

Дата добавления: 2015-06-04