Теорема Бэкингема

Обобщением полученного выше результата является следующая теорема.

Если существует величин 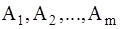, размерность которых образуется с помощью основных размерностей , то из этих величин можно построить безразмерных комплексов [1].

Для доказательства теоремы представим размерности величин 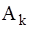в виде

и образуем из них безразмерный комплекс

. (1.3)

Подставим в это выражение размерности входящих в него величин:

.

Запишем условия безразмерности комплекса

. (1.4)

При система (1.4) не может иметь единственного решения. Для получения совокупности ее решений представим систему в виде

.

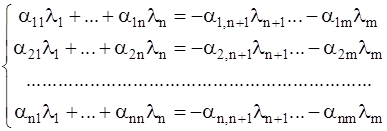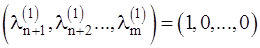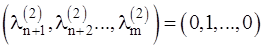Если определитель , то для каждого набора чисел , входящих в ее правую часть, можно рассчитать соответствующий набор . Построим линейно-независимую совокупность таких решений: набору соответствует решение , набору соответствует решение 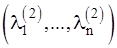, наконец, набору соответствует решение .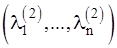

Итак, мы построили линейно независимых решений системы (1.4). Каждому такому решению, согласно (1.3), соответствует безразмерный комплекс. Таким образом, мы не только доказали возможность построения безразмерных комплексов, но и дали рецепт их построения.

Пример. Рассмотрим, как и в п.1.1, математический маятник, представляющий собой точечную массу , подвешенную на веревке длины 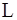в гравитационном поле с ускорением свободного падения 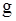. Не предполагая амплитуду колебаний 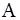малой величиной, найдем зависимость периода колебаний маятника от массы груза, длины веревки, ускорения свободного падения и амплитуды колебаний .

Для определения вида этой функции составим из величин , , 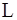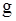и безразмерный комплекс

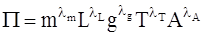. (1.5)

Подставим в это выражение размерности входящих в него величин: .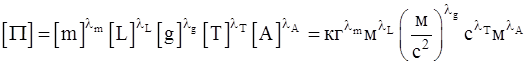

Условия безразмерности комплекса запишем в виде

,

или

. (1.6)

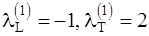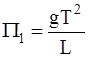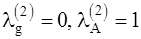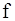В соответствии с общей теорией, положим . Тогда, согласно (1.6), . В соответствии с (1.5), получаем . Для получения второго безразмерного комплекса, положим . Тогда и . Как и следовало ожидать, из пяти величин при наличии трех основных размерностей мы построили два безразмерных комплекса. Тогда , причем вид функции не может быть определен из теории размерностей. Используя полученные выше выражения для и 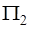, находим , или

, (1.7)

где . В случае малых колебаний 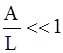и (1.7) переходит в (1.2), причем .

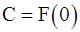Задание. Используя теорию размерностей, рассчитать зависимость периода колебаний гармонического осциллятора от его массы и жесткости .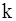

Литература

1. Бриджмен П.В. Анализ размерностей. М.-Л. 1934. 120 с.

Дата добавления: 2015-06-04