Изменение средних со временем

Теперь мы познакомим вас с еще одной интересной вещью: вы узнаете, как средние изменяются во времени. Представим на минуту, что у нас есть оператор А^, в который время явным образом не входит. Имеется в виду такой оператор, как х^ или р^.

[А исключаются, скажем, такие вещи, как оператор внешнего потенциала V (x, t), меняющийся во времени.] Теперь предста­вим, что мы вычислили < A >_ср в некотором состоянии |y>, т. е.

Как < A >_ср будет зависеть от времени? Но почему оно вообще может зависеть от времени? Ну, во-первых, может случиться, что оператор сам явно зависит от времени, например, если он был связан с переменным потенциалом типа V (x, t). Но даже если оператор от t не зависит, например оператор А^=х^, то соответствующее среднее может зависеть от времени. Ведь среднее положение частицы может перемещаться. Но как может такое движение получиться из (18.76), если А от времени не за­висит? Дело в том, что во времени может меняться само состоя­ние |y>. Для нестационарных состояний мы часто даже явно отмечали зависимость от времени, записывая их как |y(t)>. Теперь мы хотим показать, что скорость изменения < A >_ср

дается новым оператором, который мы обозначим 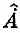. Напомним, что 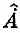это оператор, так что точка над А вовсе не означает диффе­ренцирования по времени, а является просто способом записи

нового оператора 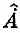, определяемого равенством

Задачей нашей будет найти оператор .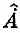

Прежде всего, нам известно, что скорость изменения со­стояния дается гамильтонианом. В частности,

Это всего-навсего абстрактная форма записи нашего перво­начального определения гамильтониана

Если мы комплексно сопряжем это уравнение, оно будет эквивалентно

Посмотрим теперь, что случится, если мы продифференцируем (18.76) по t. Поскольку каждое y зависит от t, мы имеем

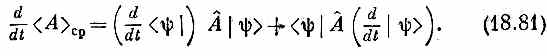
Наконец, заменяя производные их выражениями (18.78) и (18.80), получаем

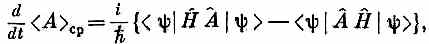
а это то же самое, что написать

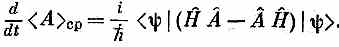
Сравнивая это уравнение с (18.77), мы видим, что

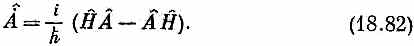
Это и есть то интересное соотношение, которое мы обещали; и оно справедливо для любого оператора А.

Кстати заметим, что, если бы оператор А сам зависел от вре­мени, мы бы получили

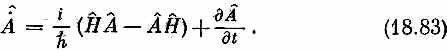
Проверим (18.82) на каком-либо примере, чтобы посмотреть, имеет ли оно вообще смысл. Какой, например, оператор соот­ветствует х? Мы утверждаем, что это должно быть

Что это такое? Один способ установить, что это такое — перейти в координатное представление и воспользоваться алгебраи­ческим оператором

. В этом представлении коммутатор равен

Если вы подействуете всем этим выражением на волновую функцию y(х)и вычислите везде, где нужно, производные, вы в конце концов получите

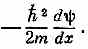
Но это то же самое, что и

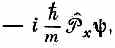
так что мы обнаруживаем, что

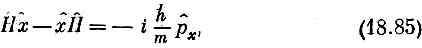
или что

Прелестный результат. Он означает, что если среднее значе­ние х меняется со временем, то перемещение центра тяжести равно среднему импульсу, деленному на массу т. Точно как в классической механике.

Другой пример. Какова скорость изменения среднего им­пульса состояния? Правила игры прежние. Оператор этой ско­рости равен

Опять все можно подсчитать в x -представлении. Напомним, что р^ обращается в d/dx, а это означает, что вам придется дифферен­цировать потенциальную энергию V (в ), но только во втором слагаемом. В конце концов остается только один член, и вы получаете

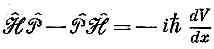
или

Опять классический результат. Справа стоит сила, так что мы вывели закон Ньютона! Но помните — это законы для операто­ров, которые дают средние величины. Они не описывают в де­талях, что происходит внутри атома.

Существенное отличие квантовой механики в том, что р^х^ не равно х^р^. Они отличаются на самую малость — на малень­кое число h. Но все поразительные сложности интерференции волн и тому подобного проистекают из того небольшого факта, что х^р^-р^х^ не совсем нуль.

История этой идеи тоже интересна. С разницей в несколько месяцев в 1926 г. Гейзенберг и Шредингер независимо оты­скали правильные законы, описывающие атомную механику. Шредингер изобрел свою волновую функцию y(х)и нашел уравнение для нее, а Гейзенберг обнаружил, что природу можно было бы описывать и классическими уравнениями, лишь бы хр-рх было равно h/i, чего можно было добиться, определив их с по­мощью особого вида матриц. На нашем теперешнем языке он пользовался энергетическим представлением и его матрицами. И то и другое — и матричная алгебра Гейзенберга и дифферен­циальное уравнение Шредингера — объясняли атом водорода. Несколькими месяцами позднее Шредингер смог показать, что обе теории эквивалентны — мы только что это видели. Но две разные математические формы квантовой механики были от­крыты независимо.

Дата добавления: 2015-06-04