Фильтрация аномальных нефтей в пористой среде

При фильтрации аномальной нефти в пористой среде линейный закон Дарси нарушается. Отклонение от линейного закона обусловлено аномалией вязкости структурированной нефти, т.е.тем, что эффективная вязкость нефти в порах породы оказывается переменной и зависящей от действующего градиента давления. При низких градиентах давления в породе фильтруется нефть с высокой вязкостью. Подвижность нефти при этом небольшая. С превышением градиента давления некоторой критической величины подвижность нефти в породе многократно увеличивается из-за соответствующего снижения вязкости нефти. При выполнении экспериментов с неньютоновскими нефтями с использованием достаточно точной аппаратуры большинство исследователей получают реологические линии (графики зависимости скорости фильтрации от градиента давления), соответствующие аномальным жидкостям. Эти линии обычно проводят через начало координат, что свидетельствует о фильтрации аномальных нефтей и при малых градиентах давления.

Для облегчения решения гидродинамических задач реальные реологические линии заменяют различными приближенными моделями. Так называемый обобщенный закон Дарси получен путем замены реологической кривой линейной зависимостью. Он обычно записывается в следующем виде:

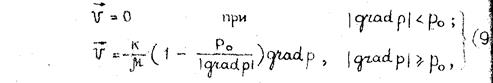
где υ - скорость фильтрации, k - коэффициент проницаемости пористой среды; µ - коэффициент динамической вязкости жидкости; р₀ – начальный градиент давления; р – переменное давление. Формула (9) представляет собой уравнение прямой линии, отсекающей на оси градиентов давления некоторый отрезок. Эту аппроксимационную константу называют начальным градиентом давления. В этом случае предполагается, что фильтрация происходит лишь при градиентах давления, превышающих р_0. Еще раз следует отметить, что такая идеализированная модель, существенно облегчая решение задач, недостаточно полно описывает важнейшие особенности фильтрации аномальной нефти в пористой среде.

Криволинейные реологические линии, соответствующие случаю фильтрации вязко-пластических систем, В.М. Ентов предлагает аппроксимировать кусочно-линейной зависимостью, ломаной линией, состоящей из нескольких отрезков.

Кусочно-линейный закон фильтрации исходит из условия осреднения скорости движения в тонких слоистых пластах, каждый из которых характеризуется мощностью h_i, коэффициентом абсолютной проницаемости k_i и параметром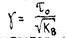

(здесь τ₀ – статическое напряжение сдвига). Считается, что в отдельном слое закон фильтрации описывается выражением (9), а средняя скорость фильтрации во всех точках пласта направлена одинаково и сохраняет постоянное значение в пределах каждого слоя. С такими допущениями кусочно-линейный закон предложен в следующем виде:

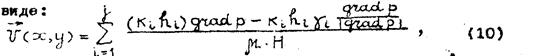
где Н – суммарная мощность всех слоев пласта; индекс i определяется из условия γ_i < |grad р| < γ_i + 1.

Преимуществом кусочно-линейного закона является то, что он позволяет описывать случай фильтрации вязко-пластической нефти в слоистом пласте. Причем осреднение скорости фильтрации сводит пространственную задачу к решению двумерной задачи движения несжимаемой жидкости в однородном пласте при условии использования закона фильтрации вида (10).

В слоистом пласте при отсутствии непроницаемых перемычек между пропластками будут перетоки жидкости. Они необходимы для выравнивания давления по вертикали. Это обстоятельство кусочно-линейным законом фильтрации не учитывается. Кроме указанных выше моделей закон фильтрации аномальной нефти может быть описан в виде степенной зависимости, а также комбинацией закона Дарси при сравнительно малых скоростях и обобщенного закона Дарси при больших скоростях фильтрации.

Из степенных законов фильтрации заслуживает внимание модель, предложенная А.Т.Горбуновым, Н.А.Ефремовой и Я.Хорнешем:

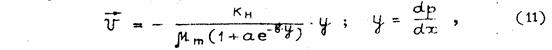
где постоянные а и в подлежат определению из результатов экспериментов.

В Уфимском нефтяном институте в течение более десяти лет проводятся опыты по фильтрации пластовых нефтей через естественные песчаники. Эксперименты выполнены с нефтями месторождений Башкирии, Татарии, Западного Казахстана и Коми. Обобщение большого количества опытов позволяет выделить реологические линии, типичные для нефтей месторождений этих районов страны, т.е. реологические линии ньютоновских жидкостей, описываемые законом Дарси, аномально-вязких систем с формой кривых С.Оствальда и реологические кривые нефтей с сверханомалией вязкости. Математическая модель фильтрации аномально-вязких нефтей с достаточной для практических целей точностью мжет быть представлена эмпирической формулой вида

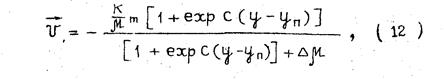
где 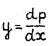- действующий градиент давления; ∆μ = μ₀ – μ_m; постоянные С и y_n определяются путем обработки результатов экспериментов.

Известно, что фильтрацию нефти, подчиняющейся закону Дарси, можно охарактеризовать одним параметром – подвижностью нефти. Для описания особенностей фильтрации аномально-вязких нефтей по аналогии с течением в узких зазорах или в капиллярах необходимо ввести четыре параметра. Это – подвижность нефти с практически неразрушенной структурой k/µ₀, простирающаяся до градиента динамического давления сдвига Н; градиент давления предельного разрушения структуры Н_m, после достижения которого фильтрация обычно происходит при постоянном значении подвижности, равной подвижности с предельно разрушенной структурой k/µ_m. Опыты показывают, что Н, как правило, соответствует началу роста подвижности нефти.

Для характеристики фильтрации нефти со сверханомалией вязкости необходимо использовать дополнительно еще один фильтрационный параметр – критический градиент давления сдвига Н_кр.

Зависимость подвижности от градиента давления называется аномалией подвижности нефти. Она характеризуется индексом аномалии подвижности (ИАП), т.е. отношением (k/µ₀)/(k/µ_m).

Фильтрационные параметры неньютоновских нефтей зависят от физических свойств пористой среды и реологических свойств жидкости. В частности, градиент динамического давления сдвига определяется предельным динамическим (статическим) напряжением сдвига нефти, проницаемостью и пористостью породы. Кроме того, на величину этого параметра оказывает влияние и структура порового пространства породы.

Б.И.Султанов, в результате обработки экспериментальных данных по фильтрации смесей различных нефтяных масел через насыпную пористую среду, для оценки начального градиента давления вязко-пластических систем предлагает следующую формулу:

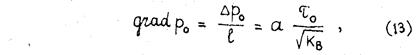
где ∆р₀ – перепад давления, расходуемый на преодоление предельного напряжения сдвига; l – длина образца породы. Коэффициент а меняется в пределах от 0,016 до 0,018.

Для аномальных пластовых нефтей нами получена следующая эмпирическая формула для расчета градиента динамического давления сдвига:

где Н и θ – соответственно градиент динамического давления сдвига в песчанике и предельное динамическое напряжение сдвига пластовой нефти; k_н – нефтепроницаемость песчаника при больших градиентах давления.

Значения параметров фильтрационных свойств аномальных пластовых нефтей изменяются в следующих пределах: градиент динамического давления сдвига от 0,002 до 0,16 кгс/см²∙м; интервал изменения Н_m в 1,3-1,5 раза больше, чем Н; индекс аномалии подвижности (ИАП) – от нескольких единиц до 50.

Дата добавления: 2015-06-04