Лекция 2 3 страница

µ= ds'/ds.

Нa карте чаще всего подписывают главный масштаб длин.

Главный масштаб площадей есть отношение, показы­вающее, во сколько раз уменьшены площадные размеры поверх­ности эллипсоида или шара при их отображении на карте. Он со­храняется на карте только в тех местах, где нет искажений пло­щадей. В других местах карты масштабы площадей больше или меньше главного и их называют частными масштабами площадей.

Частный масштаб площадей р есть отношение беско­нечно малой площади dp' на карте к соответствующей бесконечно малой площади dp на поверхности эллипсоида или шара:

р = dp'/dp.

Картографическая проекция — это математически определенное отображение поверхности эллипсоида или шара на плоскости. При этом на карте передаются положения и очертания картографируемых объектов, а также сетка меридианов и парал­лелей. Закон, определяющий картографическую проекцию, может быть выражен ее уравнениями, указанием графического построе­ния, таблицей координат и другими способами. Уравнениями картографической проекции называют два уравнения, определяющие связь между координатами точек на карте и со­ответствующих точек на поверхности эллипсоида или шара.

Координатные сетки — это картографическая, прямо­угольная, километровая и другие сетки. Картографическая сетка есть изображение меридианов и параллелей на карте. Прямоугольная сетка па карте — это координатная сетка в системе плоских прямоугольных координат в данной картогра­фической проекции. Километровая сетка — это координат­ная сетка, линии которой проведены на карте через интервалы, соответствующие определенному числу километров. Точки пересе­чения линий координатной сетки па карте называют узловыми точками.

К математической основе относят те элементы компоновки, которые обусловливают границы картографического изображения и взаимное размещение его частей. Система разграфки нужна при построении многолистных карт, при этом вводится система обозначений листов. Обозначение каждого листа определяется его номенклатурой. Номенклатура в системе разграфки определяет строго однозначное соответствие между листами и соответствую­щими им участками местности. Примером может служить раз­графка и номенклатура листов топографических карт и карт мира масштабов 1: 1 000 000 и 1 -.2 500000.

Геодезическая основа карты — это совокупность геодезиче­ских данных, необходимых для создания карты. К, ним относят параметры принятой для картографирования поверхности, систему координат и определенные в этой системе координаты опорных пунктов.

Вследствие сложности фигуры картографируемого тела ее за­меняют наиболее близко подходящей к пей математически пра­вильной поверхностью. Обычно это шар или эллипсоид (чаще всего применяют эллипсоид вращения, в отдельных случаях — трехосный эллипсоид).

Размеры шара определяют его радиусом R, положение точек на шаре — географической широтой φ и географической долготой λ (рис. 8). Широты отсчитывают от 0 на экваторе до +90° на северном полюсе и до —90° на южном полюсе. Счет долгот ведут от 0 на начальном меридиане до -И80^э в восточном направлении и до —180° в западном направлении либо от 0 до 360° в восточ­ном или западном направлениях. Международный астрономиче­ский союз (MAC) рекомендует планетографические долготы счи­тать в направлении, противоположном вращению небесного тела.

Эллипсоид вращения характеризуется большой полуосью а (экваториальной) и малой полуосью b (полярной), а также сжа­тием α и эксцентриситетами е и е'. При этом

а = (а—b)/а; е² = (а²—b²)a²; е'² = (а²— b²)/b².

Положения точек на эллипсоиде вращения определяют геоде­зической широтой В и геодезической долготой L (рис. 9), отсчитываемыми относительно нормалей к его поверхности. Начало и направление счета широт и долгот приняты так же, как на шаре.

На шаре и эллипсоиде вращения линии постоянных долгот и широт образуют сетку меридианов и параллелей, которые назы­вают географической сеткой. Эта сетка ортогональна.

Кривизна поверхности эллипсоида вращения характеризуется главными радиусами кривизны. Если в произвольно выбранной точке на поверхности восстановить нормаль к ней и через эту нормаль провести множество плоскостей, то каждая плоскость пе­ресечет поверхность но кривой линии, называемой нормальным сечением. Из них два взаимно перпендикулярных сечения будут главными, одно из которых имеет наибольшую кривизну, а дру­гое — наименьшую. Одним главным нормальным сечением явля­ется меридиан, вторым будет сечение, перпендикулярное к ме­ридиану. Его называют нормальным сечением первого вертикала. Для картографирования вычисляют радиусы кривизны меридиана М, первого вертикала N, а также средний радиус кривизны R и радиус параллели r:

; ;

;

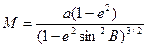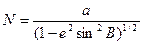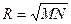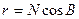
При картографировании Луны со поверхность принимают за сферу радиуса 1738 км, или, чтобы не было отрицательных вы­сот,— за сферу радиуса 1730 км. Для Венеры =6051 км, чтобы все ее высоты были положительными, можно принять —6045 км.

В разных странах применялись и применяются различные эл­липсоиды. Они отличаются как параметрами, так и исходными геодезическими датами, определяющими установку эллипсоида в теле Земли. Их называют референц-эллипсоидами или поверх­ностями относимости. В СССР в 1942 г. н качестве обязательного введен референц-эллинсоид Красовского, имеющий следующие па­раметры: a= 6378245 м; b = 6356863 м;

e² = 0,006 6934 (первый эксцентриситет); е'² = 0,0067385 (второй эксцентриситет); α = 1:298,3. Для эллипсоида Красовского колебание значений М составляет приблизительно 1 %, колебание значений N - около 1/3%, значений R — около 2/3%. Параметры референц-эллипсоидов, применяющихся в других странах, приведены в справочных сведениях. Введением исходных геодезических дат устанавливают геодезическую широту и долготу начального пункта, координаты центров основных рсференц-эллипсоидов приведены в справочных сведениях.

При отображении на карте группы материков или океана до­пустимо заменить эллипсоид шаром, т. е. приравнять широты и долготы соответствующих точек эллипсоида и шара. Искажения, которые при этом возникнут, будут в десятки или даже в сотни способов изыскания проекций, изыскание новых и совершенство­вание известных проекций, анализ проекций, изучение характера распределения искажений в проекциях и оценка их достоинства применительно к различным картам, выбор для карт проекций и математической основы в целом, разработка способов трансфор­мирования картографического изображения из одной проекции в другую, разработка способов измерений на мелкомасштабных картах в случаях, когда приходится учитывать влияние искаже­ний в проекциях, разработка способов распознавания проекций, а также разработка способов автоматизированного решения ука­занных задач.

§ 8. Искажения в картографических проекциях

Карте присущи искажения длин, площадей, углов и форм. Искажения длин на карте выражаются в том, что масштаб длин на ней изменяется при переходе от одной точки к другой, а также при изменении направления в данной точке. Вследствие этого соотношения линейных размеров географических объектов передаются с искажениями. Искажения площадей выра­жаются в том, что масштаб площадей в разных местах карты различен и нарушаются соотношения площадей различных гео­графических объектов. Искажения углов заключаются в том, что углы между направлениями на карте не равны соответствую­щим углам па поверхности и, следовательно, не равны соответ­ствующим углам на местности. Углы между линиями очертаний географических объектов искажены. Это приводит к нарушению форм самих объектов. Искажения форм заключаются в том, что фигуры объектов на карте не подобны фигурам соответствую­щих географических объектов на местности. Все виды искажений на карте связаны друг с другом, и изменение одного из них вле­чет за собой изменение других. Особый характер имеет связь между искажениями площадей и углов. Они на карте как бы на­ходятся в противоречии друг с другом и уменьшение одного из них тут же влечет за собой увеличение другого. Нет карт без искажений, однако имеются карты, в которых либо отсутствуют искажения углов, либо отсутствуют искажения площадей, либо искажения углов и площадей как бы уравновешены.

Показателем искажений длин в данной точке по данному на­правлению является частный масштаб длин р, выражаемый в до­лях главного масштаба. Он может быть больше главного (на­пример, 2,32) и меньше его (например, 0,81). Масштаб р. меняет свою величину в данной точке в зависимости от направления. По одному из направлений в данной точке масштаб длин имеет наи­большее, а по другому — наименьшее значение. Эти направления взаимно перпендикулярны, и их называют главными на­правлениями. Наибольший масштаб длин обозначим через а', наименьший — b'. Особо выделяют частные масштабы длин по ме­ридианам — т и по параллелям — п. Иногда в качестве показате­лей искажения длин берут не значения масштабов µ, a', b, m и n, а их отличие от единицы, т. е. µ—1, а'—1, b'—1, m—1 и n—1. Этот показатель называют относительным искажением длин и часто выражают в процентах. Например, если а' = 1,62, то а'—1=62%- В некоторых случаях искажение длин оценивают логарифмом частного масштаба длин, например, ln µ. Если иска­жений длин в данной точке нет, т. е. µ =1, то

ln µ = 0.

Показателем искажений площадей принимают частный мас­штаб площадей р, выражаемый в долях главного масштаба пло­щадей. Он также может

быть больше или меньше единицы. Вме­сто р используют относительный показатель р—1, часто выражае­мый в процентах, и ln р.

Величина искажения угла в данной точке карты зависит от направления сторон угла. Поэтому в качестве показателя иска­жения углов на карте принято наибольшее искажение ω. Наи­меньшее искажение углов в данной точке карты всегда равно пулю. В любой точке карты всегда имеется угол, который изобра­жается без искажений. Это угол между главными направле­ниями, который всегда равен 90°. Кроме го используется показа­тель для характеристики угла между изображениями на карте линий меридианов и параллелей. Этот угол на карте в общем случае не равен углу между меридианом и параллелью и обозна­чается 0, а его отклонение от значения угла между меридианом п параллелью на поверхности относимости, характеризующее его искажение,— ε. На шаре или на эллипсоиде вращения меридианы и параллели пересекаются под прямыми углами. Поэтому для указанных поверхностей относимости ε = 0 — 90°.

Искажения форм (как и углов) являются следствием того, что частный масштаб длин по разным направлениям различен. По­этому отношение К=а'/b' характеризует искажения форм. Чем больше отличается величина а' от b', тем сильнее вытянут в на­правлении а' контур па карте. Показатель К характеризует иска­жение форм бесконечно малых фигур. Для конечных фигур он является приближенным показателем. Он достаточно хорошо от­ражает искажения форм относительно малых географических объектов, таких, как Крымский полуостров, остров Тасмания и даже Кольский полуостров. Но для крупных объектов, таких, как материки и даже как остров Гренландия, он неточен.

Используют и другие показатели, например,

; ;

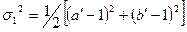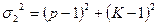Показатель σ₂ учитывает как искажения площадей, так и иска­жения форм (углов). Если его рассматривать как вектор в си­стеме координат (рис. 11), то угол α = arctg(K—1)/(р—1), опре­деляющий поворот этого вектора, характеризует соотношения искажений площадей и искажений углов: при α = 0 нет искажений углов, при отсутствии искажений площадей α = 90°; при α = 45° искажения форм и площадей уравновешены, т. е. К— 1—р—1-

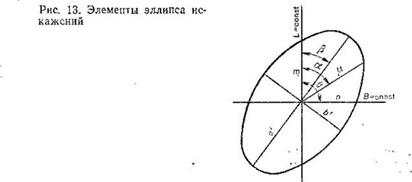
Наиболее полно все виды искажений в данной точке карты можно представить в виде эллипса искажений. Эллипс ис­кажений в данной точке карты изображает бесконечно малый круг на поверхности относимости. Его полуоси равны величинам а' и b' они ориентированы по главным направлениям. Ра­диус-вектор эллипса искажений может быть ориентирован по лю­бому направлению и определяет частный масштаб длин по этому направлению. Форма эллипса характеризует искажения углов и форм — они искажены тем больше, чем больше эллипс отличается от окружности. Площадь эллипса пропорциональна искажению площадей и тем она больше, чем больше искажены площади.

Желая показать па карте эллипсы искажений, условно прини­мают радиусы бесконечно малых окружностей на шаре или эл­липсоиде равными конечной величине (например, 5 мм в мас­штабе карты). Тогда все показываемые на карте эллипсы также примут конечные величины (рис. 12). Их можно сравнивать между собой и сопоставлять с показанными на карте, где нет искажений или отсутствует один из видов искажений. Величины и характер искажений, которые каждый эллипс демонстрирует, следует относить к точке карты, в которой находится центр эллипса.

Определяя по карте или вычисляя по формулам частные мас­штабы длин по меридианам m и параллелям n и угол между ними θ, легко вычислить параметры эллипса искажений (рис. 13). Полуоси эллипса искажений а' и b' (для шара или эллипсоида вращения) находят по формулам

; ;

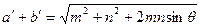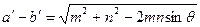Азимут на карте большой оси эллипса вычисляют по формуле

   

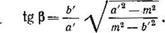
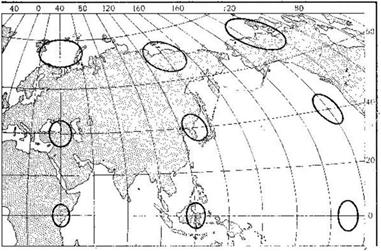
Рис. 12. Эллипсы искажений северо-восточной части миро­вой карты, построенной в поликоничсской проекции ЦНИИГАиК (вариант БСЭ)

Зная а', b', m, п, θ и β, нетрудно построить эллипс искажений в заданной точке карты. По этим данным легко найти и другие показатели искажений. Частный масштаб длин µ по произволь­ному направлению, определяемому азимутом α на карте, можно найти по формуле

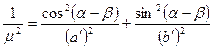
Если азимут направления задан на эллипсоиде и равен А, то

µ= a'² cos² (А — А₀) + b'² si п² (A—А ₀), где

Частный масштаб площади вычисляется по формулам

p= a'b' = тп sin θ = тп cos ε.

Для оценки максимальных искажений углов ω может быть ис­пользована любая из следующих формул:

; ;

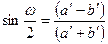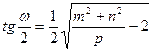В пределах карты величины искажений изменяются. В неко­торых картографических проекциях имеются центральные точки или линии, в которых искажения (обычно углов) невелики и с удалением от них вначале медленно, а затем ускоренно возра­стают. Скоростьэтого возрастания в разных направлениях мо­жет быть различной. Обычно на картах имеются точки или ли­нии, в которых искажения отдельных или всех видов отсутствуют.

Это точки и линии нулевых искажений. На карте могут быть одна- две точки или линии нулевых искажений. Места на карте с мак­симальными искажениями обычно наиболее удалены от линий пли точек нулевых искажений. Чтобы обеспечить возможно мень­шую величину максимальных искажений, точку или линию нуле­вых искажений располагают в центре карты.. Когда линия замк­нута или имеются две линии, их располагают так, чтобы удаления от них к середине и к краям карты были примерно одинаковыми. Как изменяются искажения при удалениях от точек или линий центральных или нулевых искажений, удобно показывать изоко- лами. Изоколы — линии, соединяющие точки с одинаковой ве­личиной того или иного показателя искажений. Изоколы показывают на макетах карт. Обычно в некоторых атласах, а также и учебных пособиях по математической картографии приводятся макеты с изоколами р и ω. Другой способ показа величин иска­жений

— это составление таблиц с определенным набором показа­телей искажений.

Классификация картографических проекций

По характеру искажений различают следующие картографи­ческие проекции:

Равновеликие, в которых на карте отсутствуют искажения пло­щадей, следовательно, соотношения площадей территорий пере­даются правильно. В этих проекциях карты больших территорий отличаются значительными искажениями углов и форм.

Равноугольные, в которых па карте отсутствуют искажения углов. Вследствие этого в них не искажаются также формы бес­конечно малых фигур, а масштаб длин в любой точке остается одинаковым по всем направлениям. В этих проекциях карты больших территорий отличаются значительными искажениями площадей.

Равнопромежуточные, в которых масштаб длин по одному из главных направлений сохраняется постоянным, В них искажения углов и искажения площадей как бы уравновешены.

Произвольные, в которых на карте в любых соотношениях имеются искажения и углов, и площадей.

Различают проекции по виду вспомогательной поверхности, на которую проектируется земной эллипсоид или шар при его ото­бражении па плоскости:

азимутальные, в которых поверхность эллипсоида или шара пе­реносится на касательную к ней или секущую ее плоскость;

цилиндрические, в которых поверхность эллипсоида или шара переносится на боковую поверхность касательного к ней или се­кущего се цилиндра, после чего последний разрезается по обра­зующей и развертывается в плоскость;

конические, в которых поверхность эллипсоида или шара пе­реносится па боковую поверхность касательного к ней или секу­щего ее конуса, а затем последний разрезается по образующей и развертывается в плоскость.

По ориентировке вспомогательной поверхности относительно полярной оси или экватора эллипсоида или шара различают про­екции:

нормальные, в которых ось вспомогательной поверхности сов­падает с осью земного эллипсоида или шара; в азимутальных проекциях плоскость перпендикулярна к полярной оси;

поперечные, в которых ось вспомогательной поверхности ле­жит в плоскости экватора земного эллипсоида или шара и пер­пендикулярна к полярной оси; в азимутальных проекциях плоскость перпендикулярна к нормали, лежащей в экваториальной плоскости поверхности;

косые, в которых ось вспомогательной поверхности совпадает с нормалью, находящейся между полярной осью и плоскостью экватора земного эллипсоида или шара; в азимутальных проек­циях плоскость к этой нормали перпендикулярна.

Различные положения касательной плоскости в азимутальных проекциях показаны на рис. 14;

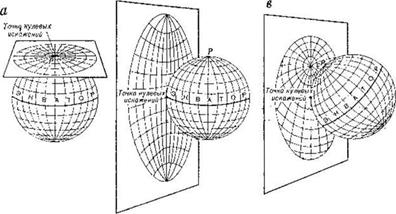
Рис. 14. Положение касательной плоскости относительно референц-поверхности и вид картографической сетки в нормальной (а), поперечной (б) и косой (в) азимутальных проекциях

на рис. 15 изображены положе­ния касательного цилиндра в цилиндрических проекциях. Кони­ческие проекции обычно применяют в нормальной ориентировке (рис. 16).

В косых и поперечных проекциях картографические сетки от­личаются от сетки нормальных проекций. В этих проекциях с нор­мальной сеткой схожи сетки вертикалов и альмукантаратов. Вер­тикалы и альмукантараты можно рассматривать как смещенные меридианы и параллели, получившиеся после перемещения гео­графического полюса в положение Q (рис. 17), которое показано в косой ориентировке. В поперечной ориентировке полюс Q лежит па экваторе, а в нормальной —совпадает с географическим по­люсом.

Положение вертикала определяется азимутом а — двугранным углом между плоскостью меридиана полюса Q и плоскостью, проведенной через нормаль в точке Q в направлении на текущую точку С (см. рис. 17). Положение альмукантарата определяется зенитным расстоянием г, отсчитываемым от полюса Q до теку­щей точки С. Вертикалы— линии, для которых a = const, альмукантараты— линии, для которых z= const. После перемещения на поверхности относимости полюса Q в географический полюс вер­тикалы совпадают с меридианами, альмукантараты — с паралле­лями. В случае шара вертикалы —дуги больших кругов, альму­кантараты — дуги малых кругов. Величины г, а называют поляр­ными сферическими координатами. Переход от широт φ и долгот λ к азимутам A и зенитным расстояниям z осуществляется по фор­мулам сферической тригонометрии:

;

;

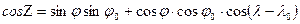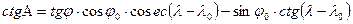В нормальной ориентировке вспомогательные поверхности ка­саются эллипсоида или шара по какой-то параллели или пересе­кают их по двум параллелям. На этих параллелях сохраняется главный масштаб длин, и их называют главными параллелями.

По виду нормальной картографической сетки прежде всего вы­деляют проекции, в которых параллели изображаются на плоско­сти линиями постоянной кривизны, т. е. прямыми линиями, окруж­ностями или их

дугами. Наиболее распространенные картографи­ческие проекции показаны на рис. 18:

а б в г

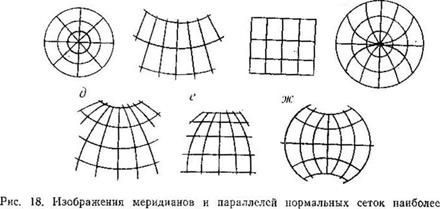
распространенных классов картографических проекций

азимутальные (рис. 18, а), в которых параллели изобража­ются концентрическими окружностями, а меридианы — прямыми, исходящими из общего центра параллелей под углами, равными разности их долгот;

конические (рис. 48, б), в которых параллели изображаются дугами концентрических окружностей, а меридианы — прямыми, расходящимися из общего центра параллелей под углами, про­порциональными разности их долгот; известны также обобщенные конические проекции, которые отличаются от конических тем, что угол между прямыми меридианами есть более сложная функция долготы;

цилиндрические (рис. 18, в), в которых меридианы изобража­ются равноотстоящими параллельными прямыми, а параллели — перпендикулярными к ним прямыми, в общем случае не равно­отстоящими; известны обобщенные цилиндрические проекции, в которых расстояния между меридианами есть более сложная функция долготы;

псевдоазимутальные (рис. 18, г), в которых параллели изобра­жаются концентрическими окружностями, меридианы — кривыми, сходящимися в точке полюса; средний меридиан — прямой;

псевдоконические (рис. 18, д), в которых параллели изобра­жаются дугами концентрических окружностей, средний мери­диан — прямой, проходящей через их общий центр, а остальные меридианы — кривыми;

псевдоцилиндрические (рис. 18, е), в которых параллели изо­бражаются параллельными прямыми, средний меридиан — пря­мая, перпендикулярная к параллелям, а остальные меридианы — кривые или прямые, наклоненные к параллелям;

полиазимутальные, в которых параллели изображаются экс­центрическими окружностями, меридианы — кривыми, сходящи­мися в точке полюса, средний меридиан — прямой;

поликонические (рис. 18, ж), в которых параллели изобража­ются дугами эксцентрических окружностей с радиусами тем боль­шими, чем меньше их

широта, средний меридиан—прямой, на которой расположены центры всех параллелей, остальные мери­дианы — кривые.

Кроме перечисленных существуют проекции, в которых парал­лели изображаются линиями переменной кривизны. Иногда про­екции, не входящие ни в один из этих классов, называют услов­ными. Иногда особо выделяют круговые проекции, в которых и меридианы, и параллели изображаются окружностями или их дугами, однако их можно рассматривать и как частный случаи поликонических проекций.

По способу получения различают проекции: перспективные, которые получают перспективным проектиро­ванием точек поверхности, чаще всего шара, па плоскость, поверхность цилиндра или конуса. Соответственно получают пер­спективные азимутальные, цилиндрические или конические про­екции. Практическое применение имеют две первые. В зависимо­сти от того, где расположен центр проектирования (точка глаза), получают проекции гномонические — проектирование из центра шара, стереографические — проектирование с поверхности шара, внешние — точка глаза за пределами шара на конечном расстоя­нии от него, ортографические — проектирование из бесконечности параллельными прямыми лучами. Если шар проектируется изну­три— получают перспективные проекции с негативным изображе­нием, при проектировании снаружи, когда из центра проектиро­вания (точки глаза) видна внешняя поверхность шара, получают проекции с позитивным изображением;

производные, которые получают преобразованием одной или нескольких ранее известных проекций путем комбинирования и обобщения их уравнений, введением в уравнения дополнительных постоянных, деформацией проекций в одном или нескольких на­правлениях, изменением их уравнений минимизацией по какому- то критерию искажений в них, аналитическими преобразованиями их уравнений и т. п.;

составные, в которых отдельные части картографической сетки построены в разных проекциях или в одной проекции, но с раз­ными параметрами — постоянными величинами, входящими в уравнения картографической проекции.

По особенностям использования различают проекции: многогранные, в которых параметры проекции подобраны для каждого листа или группы листов многолистной карты;

многополосные, в которых параметры подобраны для каждой отдельной полосы, на которые при отображении разбивается по­верхность эллипсоида или шара.

Азимутальным, коническим и цилиндрическим проекциям свой­ственны определенные системы распределения искажений. В них все искажения являются функцией лишь одной координаты— ши­роты или зенитного расстояния. Поэтому изоколы в этих проек­циях совпадают с альмукантаратами, в нормальной ориенти­ровке— с параллелями. Если вспомогательные поверхности про­екций касательны к эллипсоиду или шару, то искажения на картах нарастают по направлениям от мест касания. Так, в ази­мутальных проекциях искажения нарастают в направлениях от точки нулевых искажений, в конических —в направлениях от глав­ной параллели, в цилиндрических — в направлениях от экватора в нормальной ориентировке и в направлениях от дуги касания обозначают арабскими цифрами от 1 до 144, которые также ста­вят после номенклатуры карты масштаба 1: 1 000 000, например, М-39-120.

Лист карты масштаба 1: 100 000 положен в основу разграфки и номенклатуры карт более крупного масштаба. Один лист карты масштаба 1:100 000 разбит на 4 листа карты масштаба 1:50 000, которые обозначают заглавными буквами русского ал­фавита А, Б, В, Г, например, М-39-120-Б. Лист карты масштаба 1:50 000 содержит 4 листа карты масштаба 1:25 000, которые обозначают строчными буквами русского алфавита а, б, в, г, на­пример, М-39-120-Б-Г. Лист карты масштаба 1:25 000 содержит 4 листа карты масштаба 1:10 000, которые обозначают араб­скими цифрами 1, 2, 3, 4, например, М-39-120-Б-Г-4.

Кроме того, лист карты масштаба 1: 100 000 содержит 256 листов карты масштаба 1:5000, которые обозначают арабскими цифрами от 1 до 256, взятыми в скобки, например, М-39-120-(72). Лист карты масштаба 1: 5000 содержит 9 листов масштаба 1:2000, которые обозначают строчными буквами от а до и.

Для автоматизированного учета карт применяют цифровую номенклатуру. Буквы в номенклатуре карт масштаба 1: 1 000 000 заменены двузначными цифрами, например, вместо М-36 при­нято 13-36. Номера листов карт масштаба 1:200 000 обозначают двумя цифрами (например, вместо М-36-ХХ1 будет 13-36-21), а масштаба 1:100 000 — тремя цифрами (вместо М-36-21 будет 13-36-021). Буквы в номенклатурах листов карт масштабов 1: 500 000, I: 50 000 и 1: 25 000 заменяют соответственно циф­рами 1, 2, 3, 4, например, вместо М-36-Б будет 13-36-2.

В сдвоенных и в счетверенных листах номенклатуры также соответственно по порядку даются сдвоенными или счетверен­ными, например Р-4013-А-а, б (масштаб 1:25 000), Т-40-13, 14, 15, 16 (масштаб 1: 100 000).

В западных странах для топографических карт применяют универсальную поперечную проекцию Меркатора (UTM). Ее ос­новное отличие от проекции Гаусса — Крюгера в том, что мас­штаб длин среднего меридиана 0,99960. Получают ее двойным проектированием — эллипсоида на шар, шара на плоскость в по­перечной проекции Меркатора.

Изображение особых линий в некоторых картографических проекциях. Ортодромия—линия кратчайшего расстояния на шаре, ею является на шаре дуга большого круга, которая изобра­жается прямой в гномонической проекции. Поэтому гномонические проекции удобны для навигационных карт, особенно поляр­ных районов.

Дата добавления: 2015-06-04