Уравнение Клеро

Рассмотрим частный случай уравнения Лагранжа при . Уравнение (4.25) принимает вид

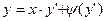(4.29)

и называется уравнением Клеро. Положив 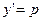,получаем:

. (4.30)

Дифференцируя по х, имеем:

, или .

Если , то р = с. Поэтому, с учетом (4.30), ДУ (4.29) имеет общее решение:

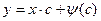. (4.31)

Если , то получаем частное решение уравнения в параметрической форме:

, . (4.32)

Это решение - особое решение уравнения Клеро: оно не содержится в формуле общего решения уравнения.

Пример 4.13. Решить уравнение Клеро .

Решение: Общее решение, согласно формуле (4.31), имеет вид 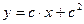. Особое решение уравнения получаем согласно формулам (4.32) в виде:

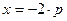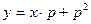, . Отсюда следует: , т.е. .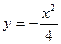

ЛИТЕРАТУРА

1) Евстигнеев Ю.Ф., Матвеева О.П. Основы математического анализа: Учебное пособие. - Спб.: Изд-во СПбГУЭФ, 2006. – 116с.

2) Письменный Д.Т. Конспект лекций по высшей математике: в 2 ч.. Ч.1/ Дмитрий Письменный.- 6-е изд. – М.:Айрис-пресс, 2008. 288с.:ил.

3) Письменный Д.Т. Конспект лекций по высшей математике: в 2 ч.. Ч.2/ Дмитрий Письменный.- 9-е изд. – М.:Айрис-пресс, 2008. 256с.:ил.

4) Общий курс высшей математики для экономистов: Учебник/Под ред. В.И.Ермакова.-М:ИНФРА-М,2000 -656с.

5) Сборник задач по высшей математики для экономистов: Учебное пособие/Под ред. В.И.Ермакова.-М:ИНФРА-М,2002 -575с.

6) Щипачёв В.С. Высшая математика. Учеб. Для вузов. – 4-е изд., стер. М., Высшая школа. 1998. – 479с:ил..

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

Студент должен выполнить контрольную работу, содержащую семь задач. Номер варианта контрольной работы соответствует последней цифре номера зачётной книжки. Номера задач каждого варианта приведены в таблице.

Номер варианта	Номера задач

Дата добавления: 2015-06-04