Фазовая скорость волны

Найдем выражение для скорости продольной волны в однородной газообразной среде. Пусть газ находится в длинном горизонтальном цилиндрическом сосуде с подвижным поршнем площадью S (см. рис.).

d v₁

Первоначально поршень находился в покое (), а в момент времени t пришел в движение и за малый промежуток времени dt приобрел скорость 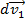, сместившись при этом на расстояние x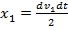₁:

. (1)

Возмущающее действие поршня за время dt распространится в газе на расстояние x₂:

x₂ = vdt (2)

и охватит область среды объемом Svdt, относительная деформация которой

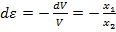(т.к. S = const),

т.е. .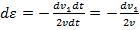

Добавочное давление dp, оказываемое поршнем на газ, можно найти по закону Гука:

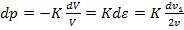. (3)

Сила, действующая на газ со стороны поршня:

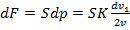, (4)

а импульс этой силы:

(5)

приводит к изменению импульса газа:

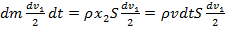, (6)

где ρ – плотность газа.

Из II закона Ньютона в импульсной форме следует, что уравнения (5) и (6) равны: 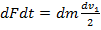. Тогда

,

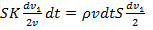следовательно,

,

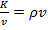откуда получаемвыражение для фазовой скорости продольной волны:

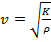. (7)

Аналогичные вычисления для поперечных волн приводят к выражению для фазовой скорости:

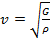, (8)

где G – модуль сдвига.

Скорость упругих волн в идеальном газе зависит от их частоты. Такое явление называется дисперсией волн. Возможны два предельных случая.

Если частота достаточно мала, то процесс деформации можно считать изотермическим, т.е. pV = const; Vdp + pdV = 0, откуда dp = – p 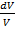.Поскольку, согласно закону Гука, dp = – К 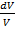, то K = p. Следовательно, фазовая скорость волны: 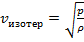. Выразив давление p из уравнения Клайперона-Менделеева: 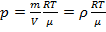, получим выражение для фазовой скорости волны при изотермической деформации:

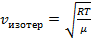. (9)

При больших частотах процесс считается адиабатическим, pV ^γ = const (уравнение Пуассона); V ^γdp + γ V ^{γ –1}pdV = 0; V ^{γ –1}(Vdp + γ pdV) = 0; Vdp + γ pdV = 0; dp = – γ p 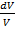; K = γ p. Таким образом, получим выражение для фазовой скорости волны при адиабатической деформации:

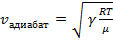. (10)

Опыты показывают, что скорость звука, т.е. слышимых звуковых волн, частота которых лежит в пределах от 16 Гц до 20 кГц, в газах практически не зависит от частоты и соответствует формуле (10).

Дата добавления: 2015-06-04