Теоретичні відомості

Загальне призначення множинної регресії полягає в аналізі зв'язку між декількома незалежними змінними, що називаються також регресорами, або предикторами, й залежною змінною.

Пряму лінію для двох змінних задають рівнянням

Y = b₀ + b₁X,

де X – незалежна змінна, Y – залежна змінна, b₀ – вільний член рівняння, b₁ –кутовий коефіцієнт, що називають регресійним.

Використавши отримане рівняння, можна розрахувати окремі значення залежної змінної.

На рис. 4.1 показано довірчий інтервал (90, 95 і 99%), побудований для двовимірного регресійного рівняння.

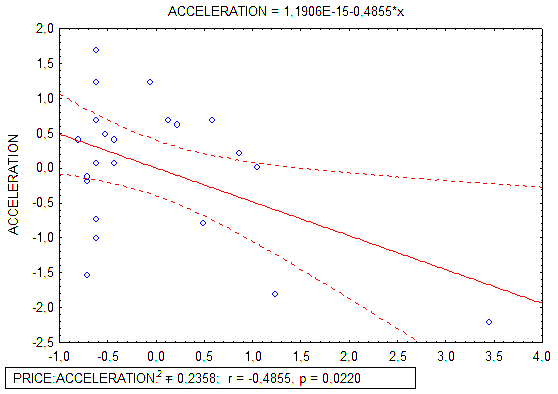
Рис. 4.1. Графік розсіювання з регресійною прямою
та 95%-ним довірчим інтервалом

Звичайно існує розкид спостережуваних точок щодо пригнаної прямої. Відхилення точки від завбаченого значення називають залишком (або помилкою).

Рівняння лінійної множинної регресії має вигляд

,

де X₁ … X_p – незалежні змінні, Y – залежна змінна, b₀ – вільний член рівняння, b₁ … b_p – регресійні коефіцієнти.

У множинній регресії припускають, що залишки підпорядковуються закону нормального розподілу. Регресійні коефіцієнти визначають, наскільки кожна незалежна змінна обумовлює прогнозування залежної змінної. Таку кореляцію називають частковою. Якщо зв'язок між змінними X і Y відсутній, то відношення залишкової мінливості змінної (дисперсії залишків) D_ε до вихідної дисперсії D_y дорівнює одиниці. Коефіцієнт детермінації, що визначає ступінь залежності змінних, розраховують за формулою

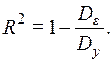
Якщо нелінійність зв'язку є очевидною, то необхідно перетворити змінні. Варто використати, принаймні, від 10 до 20 спостережень за кожною змінною, у протилежному випадку оцінювання регресійної лінії буде неточним.

Проблема мультиколінеарності є загальною для багатьох методів кореляційного аналізу. Ця проблема може виникнути, якщо аналізу підлягає багато змінних. У цьому випадку змінні використовувати недоцільно, тому що дані будуть надлишковими. Існують статистичні індикатори надмірності (толерантність, напівчастне та ін.), а також способи для боротьби з надмірністю (наприклад, метод гребеневої регресії).

Дата добавления: 2015-06-04