Задачі для самостійного розв’язку

.

Приклад 22. Знайти число всіх таких слів довжини mn у n - буквеному алфавіті, у котрих кожна буква алфавіту зустрічається m разом.

Розв’язок. Число слів дорівнює числу перестановок із повтореннями

.

Приклад 23. Скількома способами множина з n елементів може бути розбите на S підмножин, із яких перше містить 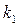елементів, друге - 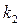елементів, …, s – e - - елементів.

Число способів дорівнює числу перестановок із повтореннями

.

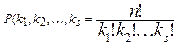Задачі для самостійного розв’язку

1. Скільки тризначних чисел можна скласти з цифр 1, 2, 3, 4, 5?

2. Скільки є п'ятизначних чисел, що діляться на 5?

3. Скільки є двохзначних чисел, у яких обидві цифри парні?

4. Скільки є п'ятизначних чисел, у яких усі цифри непарні?

5. У селищі живуть 1500 жителів. Довести, що принаймні двоє з них мають однакові ініціали.

6. На зборах повинні виступити 5 чоловік: А, Б, У, Г, Д. Скількома способами можна розташувати їх у списку за умови, що Б не повинний виступати до того, як виступить А?

7. Четверо студентів складають іспит. Скількома способами можуть бути поставлені їм оцінки?

8. У кімнаті n лампочок. Скільки усього різних способів освітлення кімнати, при яких горить рівно k лампочок?

9. Є n деталей, із них m із дефектом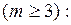

1) скількома способами можна вибрати дві деталі так, щоб одна з них була з дефектом, а інша – доброякісна?

2) скількома способами можна вибрати п'ять деталей так, щоб із них дві були доброякісними, а три - із дефектом?

3) скількома способами можна вибрати R деталей так, щоб серед них було рівно S із дефектом?

10. У студентській групі кожний вивчає англійську або французьку мова. Англійську мову вивчають 18 чоловік, французьку - 13 чоловік, а обидві - 6 чоловік. Скільки студентів у групі?

11. Із 100 студентів англійську мову знають 28 студентів, німецьку - 30, французьку - 42, англійську та німецьку - 8, англійську та французьку - 10, німецьку та французьку - 5, усі три мови знають три студенти. Скільки студентів не знають жодної з трьох мов?

12. Скільки різних слів можна скласти, переставляючи букви слова “математика”?

13. Скількома способами можна переставляти букви слова “город” так, щоб три букви “о” не стояли поруч?

14. У кімнаті студентського гуртожитку живуть троє студентів. У них є 4 чашки, 5 блюдець і 6 чайних ложок (усі чашки, блюдця і ложки відрізняються одне від одноти). Скількома способами вони можуть накрити стіл для чаювання (кожний одержує одну чашку, одне блюдце та одну ложку)?

15. Із групи, що складається з 7 чоловіків і 4 жінок, треба вибрати 6 осіб так, щоб серед них було не менше 2 жінок. Скількома способами це можна зробити?

16. У кондитерському магазині продаються 4 сорти тістечок. Скількома способами можна купити 7 тістечок? Скількома способами можна купити 3 тістечка? Скількома способами можна купити 3 різних тістечок?

17. На студентському вечорі присутні 12 дівчат та 12 юнаків. Скількома способами можна вибрати 4 пари для танцю?

18. Студенту необхідно скласти 4 іспити протягом 8 днів. Скількома способами це можна зробити?

Тема 4. Логічні операції та їхні властивості

Приклад 24. Побудувати істинностну таблицю складного висловлення, заданого формулою .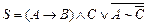

Очевидно, таблиця істиности буде містити 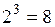рядків. Дужки порушують природний порядок операцій - , указує на те, що спочатку потрібно виконати імплікацію, використовуючи таблицю істинності імплікацій, потім потрібно знайти кон’юнкцію (), з огляду на таблицю істинності операції кон’юнкції. Далі треба виконати заперечення 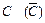з урахуванням таблиці істиности заперечення, еквівалентність 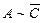і заперечення Заключною операцією в побудові таблиці істиности для S буде диз'юнкція двох висловлень:

Порядок і результати виконання логічних операцій наведені у таблиці:

A	B	C

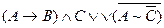
Отже, формула S задає висловлення, яке істинне на таких наборах значень елементарних висловлень: A=1, B=1, C=1 (усі три елементарних вислов

A=0, B=1, C=1 (A - хибне, B і C - істинні);

A=0, B=1, C=0 (У - істинне, A, C - хибні);

A=0, B=0, C=1 (С - істинне, A, B - хибні);

A=0, B=0, C=0 (усі три висловлення хибні).

Приклад 25. Довести рівносильність формул

1. Таблиця істинності для формули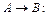

A	B

2. Побудуємо таблицю істинності для формули

A	B

Таблиці істинності збігаються, отже формули рівносильні.

Приклад 26. Показати рівносильність формул

1. Для формули 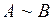таблиця істинності:

A	B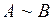

2. Побудуємо таблицю істинності для формули :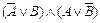

A	B			B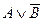

Порівнюючи таблиці, бачимо, що значення істини та хибності обидва висловлення приймають на тих же самих наборах істинності і хибності елементарних висловлень А і В. Виходить, формули рівносильні.

Тема 5. Перевірка правільности міркувань

Приклад 27. Треба встановити, чи правильне міркування:

“Якщо функція на даному інтервалі неперервна і має різні знаки на його кінцях, то усередині даного інтервалу функція обертається в нуль. Функція не обертається в нуль усередині даного інтервалу, але на кінцях інтервалу має різні знаки. Отже, функція розривна”.

У запропонованому для розгляду міркуванні посилки і висновок складаються з таких елементарних висловлень:

А - функція неперервна на даному інтервалі;

В - функція має різні знаки на кінцях інтервалу;

С - функція обертається в нуль усередині даного інтервалу.

Використовуючи ці позначення, запишемо посилки і висновок у виді формул:

_______________________________

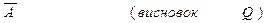
Міркування є вірним, якщо імплікація тотожно істинна.

Для перевірки правильності міркувань будуємо таблицю істинності:

А	В	С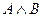

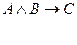
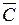
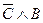
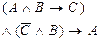
Переконуємося, що міркування є вірним. Проведемо перевірку правильності цього міркування методом від супротивного. Припустимо, що висновок Q хибний. Покажемо, що в цьому випадку кон’юнкція посилок - помилкова, тобто контрапозиція 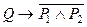тотожно істинна.Справді, якщо 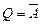- хибна, то А - істинне. Нехай 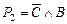- істинне, тоді В - істинне, 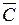- істинне, тобто С - хибне, але в цьому випадку посилка 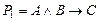приймає значення хибне, тому що ми одержали, що 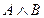- істинне, а С - хибне.

Тема 6. Нормальні форми алгебри висловлень.

Приклад 28. Побудувати КНФ для формули алгебри висловлень:

1. Позбудемося від знаків імплікації, використовуючи рівносильні формули:

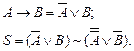
2. Позбудемося від знака еквівалентності, використовуючи рівносильну формулу

3. Позбудемося від знака заперечення, що ставиться до виразів, які складаються більш ніж з однієї змінної, використовуючи закони де Моргана

4. Позбудемося від подвійних і потрійних заперечень:

5. Застосуємо закони дистрибутивності

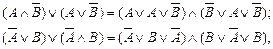
одержимо 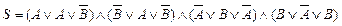, що є КНФ для даної формули S.

6. Використовуючи властивості і 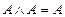, спростимо КНФ для S:

Отже, формула S - здійснена.

Приклад 29. Встановити тип формули

Визначимо КНФ для заперечення S:

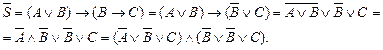
КНФ для 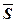не задовольняє умову теореми 1, отже формула S - здійсненна.

Приклад 30. Дана КНФ 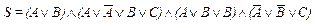. Побудувати СКНФ.

1.

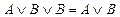
2.

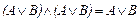
3.

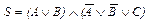
4.

Визначення ДКНФ і ДДНФ дозволяють для кожної формули алгебри висловлень, приведеної до ДНФ або КНФ, побудувати її ДДНФ або ДКНФ.

Приклад 31. Задана ДНФ, призвести до ДДНФ:

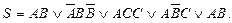
1. Перший і останній доданки однакові. На підставі властивості операції диз'юнкції 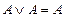один із додатків можна відкинути.

2.

3.

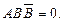
Одержимо

Тепер виконані умови 1-3. Щоб задовольнити умову 4, випливає:

Отже

Тепер умова 4 виконано, але з'явилися однакові доданки. Виключивши їх, отримаємо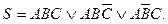

Приклад 32. Дана КНФ Побудувати ДКНФ.

1.

2.

3.

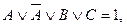
отже

4. 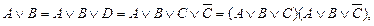отже

1. Показати рівносильність формул

а)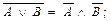

б)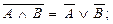

в)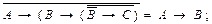

г)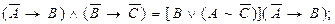

д)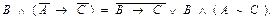

2. Перевірити правильність міркування 3 способами.

1. Якщо 2 - просте число, то це найменше просте число. Якщо 2 - найменше просте число, те 1 не є простим числом. Число 1 не є простим числом. Отже, 2 - просте число.

2. Якщо всі сторони чотирикутника рівні між собою, то він є паралелограмом тоді і тільки тоді, коли його діагоналі діляться в точці перетину навпіл. Протилежні сторони чотирикутника попарно рівні. Отже, його діагоналі діляться в точці перетину навпіл.

3. За допомогою ДНФ і КНФ визначити тип формул:

а)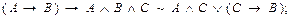

б)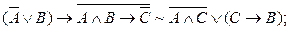

в)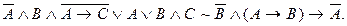

4. За допомогою СДНФ і СКНФ установити рівносильність формул

а)

б)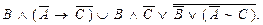

Тема 7. Операції над графами.

Приклад 33. 1. Знайти граф G (X, F), що є об'єднанням графів G1 (X1, F1) і G2 (X2, F2

G1 (X1, F1) G2 (X2, F2)

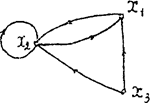
Рисунок 2. Вихідні графи.

X1 = { x₁, x₂, x₃ }; X2 = { x₁, x₂ };

F (x₁) = { x₂ }; F2 (x₁) = { x₁ };

F (x₂) = F (x₃) = { x₁, x₂ }; F2 (x₂) = { x₁, x₂ }.

Знаходимо, що X = X1 U X2 = { x₁, x₂, x₃ }; F = F1 U F2; F (x₁) = F (x₂) = F (x₃)={ x₁, x₂ }.

Геометричне зображення графа G (X, F):

Рисунок 3. Об'єднання графів G1 і G2

2. Знайти граф G (X, F), що є перетином графів G1 (X1, F1) і G2 (X2, F2

Одержуємо X = X1 ∩ X2 = { x₁, x₂ }; F = F1 ∩ F2; F (x₁) = Æ; F (x₂) = { x₁, x₂ }.

Геометричне зображення графа G:

Рисунок 4. Перетин графів G1 (X1, F1) і G2 (X2, F2)

Приклад 34. Задані два графа. Знайти G (X, F) = G1 (X1, F1) ´ G2 (X2, F2).

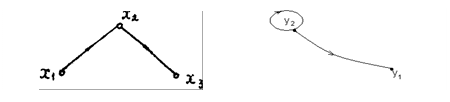G1 (X1, F1) G1 (X2, F2)

Рисунок 5. Вихідні графи.

Розв’язок. Результатний граф G (X, F), де X = { z₁, z₂, z₃, z₄, z₅, z ₆ }

z₁ = (x₁, y₁); z₂ = (x₁, y₂); z₃ = (x₂, y₁); z₄ = (x₂, y₂); z₅ = (x₃, y₁); z₆ = (x₃, y₂);

F1 (z₁) = Æ, тому що F1 (x₁) = { x₂ }, а F2 (y₁) = Æ; F (z₂) = { z₃, z₄ }, тому що F1 (x₁) = { x₂ }, а F2 (y₂) = { y₁, y₂ }; F (z₃) = Æ; F (z₄) = { z₅, z₆ }; F (z₅) = Æ; F (z₆) = Æ.

Рисунок 6. Декартовим(прямий) добуток графів G1 (X1, F1) і G2 (X2, F2)

Тема 8. Максимальний потік у мережі.

Приклад 35. Розглянемо граф, зображений на Рисунке7. Потрібно знайти максимальний потік від х ₁ до x_y.

Розв’язок. Як початковий візьмемо потік із нульовими значеннями на всіх дугах x _ij = 0, "_ij. Пропускні спроможності дуг q_ij зазначені на Рисунке 7.

Крок 1. Припишемо вершині x_i позначку (+ x₁, ¥).

Крок 2. а) множина непозначених вершин: { x_j | x_j Î F (x₁), x _1j < q_1j } = { x₁, x₄ }.

Вершині x₂ приписується позначка (+ x₁, min (¥, q₁₂ - x ₁₂)) = (+ x₁, min (¥, 14-0) = (+ x₁, 14).

Вершині x₄ приписується позначка (+ x₁, min (¥, q₁₄ - x ₁₄)) = (+ x₁, min (¥, 23-0) = (+ x₁, 23).

Рисунок 7. Вихідний граф.

б) множина непозначених вершин: { x_j | x_j Î F^-1 (x₁), x _j1 > 0} = Æ.

Отже, x₁ позначена і переглянута, x₂ і x₄, позначені і не переглянуті, а всі інші вершини не позначені. Повторюємо крок 2, переглядаючи вершину x₂ (вершини переглядаються в порядку зростання їхніх номерів). Множина непозначених вершин:

a) { x_j | x_j Î F (x₂), x _2j < q_2j } = { x₃ }.

Позначка для x₃: (+ x₂, min (14, q₂₃ - x ₂₃)) = (+ x₁, min (14, 10-0) = (+ x₂, 10).

б) Множина непозначених вершин { x_j | x_j Î F^-1 (x₂), x _j2 > 0} = Æ.

Тепер вершини х₁ і х₂ позначені і переглянуті, а x₃, x₄ позначені і не переглянуті.

Переглядаємо вершину x₃.

а) множина непозначених вершин { x_j | x_j Î F (x₃), x _3j < q_3j } = { x₅, x₈ },

для x₅ позначкою є (+ x₃, min (10, 12-0) = (+ x₃, 10).

для x₈ позначкою є (+ x₃, min (10, 18-0) = (+ x₃, 10).

Переглядаючи x₄, ніяких позначок розставити не можна, тому що всі суміжні з x₄ вершини вже позначені. Переглядаючи x₅, одержимо такі позначки:

для x₆ - (+ x₅, min (10, 25-10) = (+ x₅, 10);

для x₇ - (+ x₅, min (10, 4-0) = (+ x₅, 4).

Переглядаючи x₇ одержимо позначку для x₉ - (+ x₅, min (4, 15-0) = (+ x₅, 4).

Переходячи до кроків 4 і 5, отримаємо

x = x₉ - відповідна позначка (+ x₇, 4). Потік x ₇₉ змінюємо, додаючи d (x₉) = 4, x ₇₉ = 0 + 4 = 4;

x = x₇ - відповідна позначка (+ x₅, 4).Потік x₅₇ = 0 + 4 = 4;

x = x₅ - відповідна позначка (+ x₃,10). Потік x ₃₅ = 0 + 4 = 4;

x = x₂ - відповідна позначка (+ х_{1 ,} 14).Потік x ₁₂ = 0 + 4 = 4.

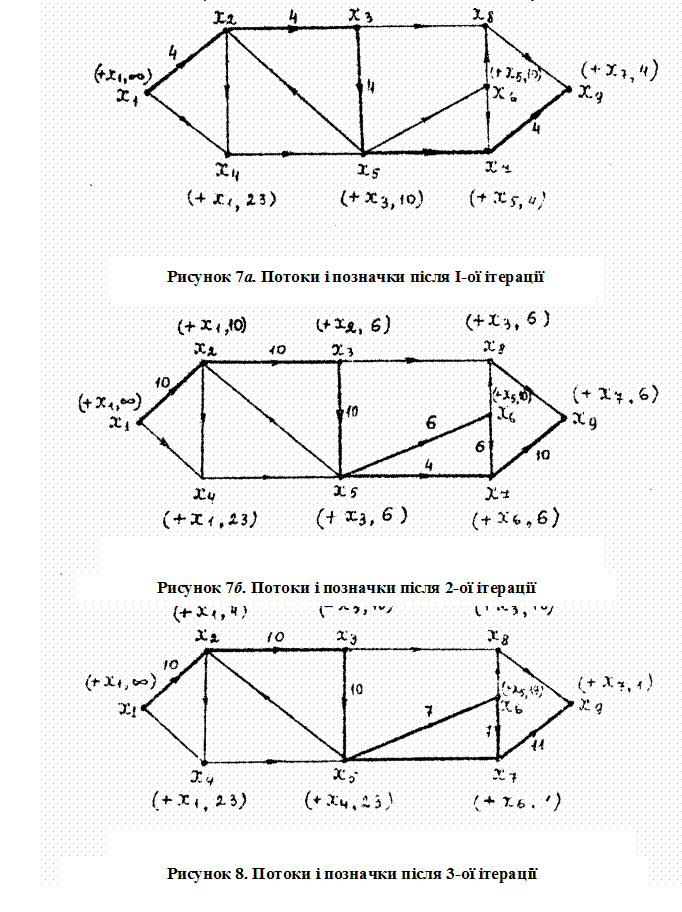
Всі інші значення потоків залишилися рівними нулю. Потік наприкінці кроку 5 і позначки вершини до їхнього стирання на кроці 6 показані на Рисунок 7 а. Стираючи позначки у вершин і повертаючись до кроку 1 для другого проходу, одержимо такі нові позначки: для x₁ - (+ x₁,¥);

для x₂ - (+ x₁, min (¥, 14-4) = (+ x₁, 10);

для x₃ - (+ x₁, min (¥, 23-0) = (+ x₂, 23).

Вершина x₁ позначена і переглянута. Переглядаючи вершину x₂, одержимо позначку

для x₃ - (+ x₂, min (10, 10-4)) = (+ x₂, 6).

Вершина позначена і переглянута. Переглядаючи вершину x₃, одержимо позначки:

для x₅ - (+ x₃, min (6, 12-4)) = (+ x₃, 6);

для x₈ - (+ x₃, min (6, 18-0)) = (+ x₃, 6).

Вершина x₃ позначена і переглянута. Переглядаючи вершину x_{5 ,} одержимо позначки:

для x₆ - (+ x₅, min (6, 25-0)) = (+ x₅, 6).

Вершина x₅ позначена і переглянута. Переглядаючи вершину x_{6 ,} знаходимо, що позначкою для x₇ будет (+ x₆, min (6, 7-0)) = (+ x₆, 6). Тепер вершина x₆ позначена і переглянута.

Позначка для x₉: (+ x₇, min (6, 15-4)) = (+ x₇, 6).

Кроки 4 і 5. Нові потоки збільшилися в такий спосіб:

x ₇₉ = 4 + 6 = 10; x₆₇ = 0 + 6 = 6; x ₅₆ = 0 + 6 = 6;

x ₃₅ = 4 + 6 = 10; x ₂₃ = 4 + 6 = 10; x ₁₂ = 4 + 6 = 10.

Всі інші значення потоку не змінилися. Новий потік і позначки вершин до стирання показані на Рисунок 7 б.

Аналізуючи всі етапи визначення потоків, одержуємо після кожного проходу алгоритма потоки і позначки, зображені послідовно на Рисунок 8-11. Алгоритм закінчує роботу, коли тільки вершина x₆ може бути позначена. Потік, що відповідає дугам

(x₂, x₃), (x₃, x₆), (x₆, x₇), (x₆, x₈), (x₅, x₇) є максимальним із значенням 10 + 0 + 8 + 7 + 4 = 29.

Тема 9. Найкоротший шлях у мережі.

Приклад 35. Розглянемо граф, зображений на Рисунке 12, де кожне неорієнтоване ребро розглядається як пару протилежно орієнтованих дуг рівної ваги. Матриця С ваг приведена нижче.

Рисунок 12. Вихідний граф.

Матриця ваг (C= (с_ij))

	x1	x2	x3	x4	x5	x6	x7	x8	x9
x1
x2
x3
x4
x5
x6
x7
x8
x9

Крок 1. l (x₁) = 0 - позначка постійна, l (x₁) = р, " x_i ¹ x_{i ,} p = x_i

Перша ітерація

Крок 2. F (p) = { x₂, x₇, x₈, x₉ } множина вершин, в які є дуга з x₁. Позначки l (x₂), l (x₇), l (x₈), l (x₉) - тимчасові і рівні ¥. Обновляємо позначку вершини x₂, для цього находим

min { l (x₂), l (p) + c (p, x₂)}. Тому що l (x₂) = ¥, а l (p) = 0, с ₁₂ = 10, то одержуємо

min {¥, 0+10}= 10, виходить, l (x₂) = 10.

Аналогічно знаходимо

l (x₇) = min {¥, 0+3}= 3; l (x₈) = min {¥, 0+6}= 6; l (x₉) = min {¥, 0+12}= 12.

Крок 3. Знаходимо min {l(x_i)}, тобто

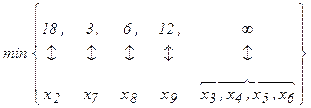відповідає x₇

Крок 4. x₇ одержує постійну позначку l (x₇) = 3; p = x₇.

Крок 5. Не всі вершини мають постійну позначку, тому переходимо до кроку 2. Позначки на початку другої ітерації показані на Рисунке 13. Із знаком + показані постійні позначки.

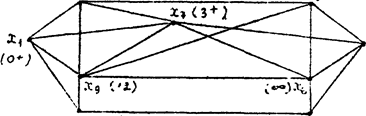
Рисунок 13. Перша итерація.

Друга ітерація

Крок 2. F (p) = F (x₇) = { x₂, x₄, x₆, x₉ } - усі позначки тимчасові.Обновляємо позначку вершини x₂. З огляду на те, що l (x₂) = 10, l (p) = 3, C₇₂ = 2, знаходимо min {10, 3+2}= 5, тобто l (x₂) = 5.

Аналогічно l (x₄) = min {¥, 3+4}= 7; l (x₆) = min {¥, 3+14}= 17; l (x₉) = min {12, 3+24}= 12.

Крок 3. Знаходимо min {l(x_i)}, тобто

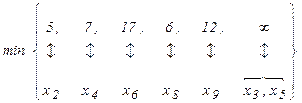відповідає x₂

Крок 4. x₂ одержує постійну позначку l (x₂) = 5; p = x₂.

Крок 5. Перейти до кроку 2.

Обчислення по кожній ітерації зручно звести в таблицю, наведену на Рисунок 14.

	x1	x2	x3	х4	x5	x6	x7	x8	х9
х1^+	0^+	¥	¥	¥	¥	¥	¥	¥	¥
х7^+			¥	¥	¥	¥	3^+
х2^+		5^+	¥		¥
х8^+					¥			6^+
х4^+				7^+

Рисунок 14. Сводная таблиця всіх итерацій.

Перший рядок таблиці відповідає початковим позначкам вершин. Показані зліва в таблиці вершини зі знаком + одержують постійні позначки, а числа зі знаком + у рядку таблиці відповідають min { l (x_i)}. Після першої ітерації постійну позначку одержала вершина x₇, а min { l (x_i)} = 3. Після того, як вершина x₇ одержала постійну позначку, числа в стовпчику, що відповідає х₇ залишаються незмінними.

На четвертій ітерації постійну позначку одержує х₄, тобто р = х₄, а х₄ відповідає стокові t. Таким чином, алгоритм закінчує роботу, довжина найкоротшого шляху дорівнює

l (p) = l (x₄) = 7.

Для знаходження найкоротшого шляху використаємо співвідношення:

l (x_i') + c (x_i', x_i) = l (x_i), (*)

x_i' - вершина, що безпосередньо передує вершині x_i у найкоротшому шляху від S до x_i. Якщо існує декілька найкоротших шляхів від S до якоїсь іншої вершини, то при деякій фіксованій вершині x_i' співвідношення (*) буде виконуватися більш ніж для однієї вершини x_i. У цьому випадку вибір може бути або довільним (якщо потрібний якийсь один найкоротший шлях між S і x_i), або таким, що розглядаються всі дуги, які входять в якийсь із найкоротших шляхів.

Знайдемо найкоротший шлях від x₁ до x₂. Для цього знаходимо вершину х ₂' із співвідношення: l (x₂') + c (x₂', x₂) = l (x₂) = 5.

У стовпчику, x₂ матриці С, і в останньому рядку таблиці (див. Рисунок 18) знаходимо числа, сума яких дорівнює 5. У стовпчику x₂ матриці С містяться числа 10, 18, 2, 13. Потрібно взяти число 2, що відповідає вершині x₇

l (x₇') + c (x₇', x₇) = 3 + 2 = 5, тобто вершиною, що задовольняє співвідношенню (*), є x₇.

Поклавши x_i = x₇, знаходимо вершину безпосередньо передуючу x₇ у найкоротшому шляху від x₁ до x₂. Вершина x₇', повинна задовольняти співвідношення: l (x₇') + c (x7', x₇) = 3.

У стовпчику x₇ матриці С містяться числа 3, 2, 4, 14, 24. Можна брати або 2, або 3. Візьмемо число, рівне 2, йому відповідає вершина x₂, l (x₂) + c (x₂, x₇) = 2 + 5 ¹ 3, виходить, x₂ не задовольняє співвідношення (*). Залишається вершина x₁, l (x₁) + c (x₁, x₇) = 0 + 3 = 3. Таким чином, єдиною вершиною яка задовольняє співвідношення (*), є x₁.

Отже, найкоротшим шляхом від x₁ до x₂ є шлях (x₁, x₇, x₂). Знаходимо найкоротший шлях від x₁ до x₃, відзначимо, що l (x₃) = 23. У стовпчику x₃ матриці С містяться числа 18, 25, 20. Придатним числом є 18, якому відповідає x₂.

l (x₂) + c (x₂, x₃) = 5 + 18 = 23 = l (x₃).

Виходить, найкоротший шлях від x₁ до x₃ - це шлях (x₁, x₇, x₂, x₃).

Аналогічно можна знайти найкоротші шляхи від вершини x₁ до будь-якої вершини мережного графа. Ці дуги зображені на Рисунке 15 жирними лініями. З Рисунку 15 видно, що найкоротший шлях від x₁ до x₄ - це шлях (x₁, x₇, x₄).

Рисунок 15. Найкоротший шлях.

Задачі для самостійного рішення

1. Є граф G (X, F): X = { x₁, x₂, x₃, x₄, x₅ }; F (x₁) = { x₄ }; F (x₂) = { x₁, x₄ }; F (x₃) = { x₄, x₅ };

F (x₄) = { x₁, x₅ }; F (x₅) = { x₁, x₃,}.

Зобразити цей граф графічно і скласти для нього матриці суміжності і інциденцій.

2. Є граф G (X, F): X = { x₁, x₂, x₃, x₄ }; F (x₁) = { x₃ }; F (x₂) = { x₃, x₄ }; F (x₃) = { x₁, x₄ }; F (x₄) = { x₃ }.

Зобразити цей граф графічно і скласти для нього матриці суміжності та інциденцій.

3. Є граф

Рисунок 16. Вихідний граф.

Записати цей граф графічно як відображення множини вершин у себе. Скласти для цього графа матриці суміжності та інциденцій.

4. Дано матрицю інциденцій деякого графа:

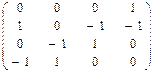
Записати цей граф аналітично як відображення множини вершин у себе. Зобразити граф графічно і скласти для нього матриці суміжності.

5. Є два графи G1 і G2:

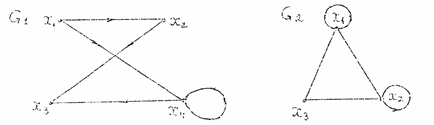
Рисунок 17. Вихідні графи.

Знайти G1 U G2, G1 ∩ G2 і матриці суміжності результуючих графів.

6. Визначити максимальний потік у мережі

Рисунок 18. Вихідний граф.

7. Визначити найкоротший і критичний шляхи в графі x₁ до x₁₂.

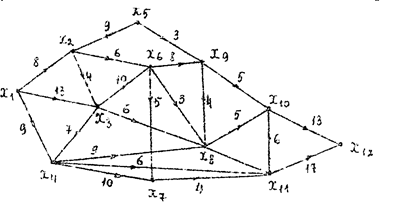
Рисунок 19. Вихідний граф.

Список літератури

1. В.И.Донской. Дискретная математика. – Симферополь: «Сонат», 2000.

2. А.Ф. Кравчук. Основи дискретної математики. – Київ – НМК ВО – 1992.

3. Логіка: Підруч. Для вузів – Знаня Жеребкін В.Є. – К.: - 1999.

4. Алферова З.В., Езжева В.П. Применение теории графов в економических расчетах. -М.: Статистика, 1971.

5. Виленкин Н.Я. Комбинаторика. – М.: Наука, 1969.

6. В.А. Горбатов Основы дискретной математики. – М.: Высшая школа, 1986.

7. Ежов И.И., Скороход А.В., Ядренко М.И. Элементи комбинаторики. – М.: Наука, 1977.

8. Кузин Л.Т. Основы кибернетики. -М.: Енергия, 1972. - Т.2

9. Кристофидес Н. Теория графов. -М.: Мир, 1978.

10. В. Липский. Комбинаторика для программистов – М.: Мир, 1988. – с.204.

11. Э. Мендельсон. Введение в математическую логику. - М.: Наука, 1976.

12. Харари Ф. Теория графов. -М.: Світ, 1973.

13. Андриенко В.М., Будорацкая Т.Л. Методические указания по дисциплине “Дискретная математика”. – Одесса: ОГПУ, 1999.

Дата добавления: 2015-06-04