Измерение частоты и сдвига фаз синусоидальных сигналов. Фигуры Лиссажу

Осциллограф позволяет определить значение частоты и сдвиг фаз синусоидальных сигналов относительно друг друга. Измерение частоты и сдвига фаз производится сигнальным методом, называемым методом фигур Лиссажу.

Измерение неизвестной частоты синусоидального сигнала при помощи фигур Лиссажу производится следующим образом. Внутренняя развертка в данном методе не применяется; при этом переключатель осциллографов “Диапазоны частот” устанавливается в положение “0” - внутренняя развертка отключается.

Сигнал, частота f_x которого неизвестна, подается на один из входов осциллографа, например на “вход Х”. Сигнал известной частоты f₀ от эталонного генератора подается на другой вход осциллографа - “вход У”. Следовательно, электронный луч осциллографа под действием двух сигналов передвигается по сложной кривой, описывая на экране определенную фигуру - фигуру Лиссажу. Форма этой фигуры зависит от отношения амплитуд, частот и начальных фаз сравниваемых сигналов.

Рис.3а 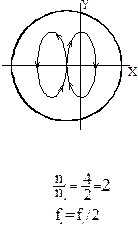Рис.3б

Рис.3в Рис.4г Рис.4д

Образование фигуры Лиссажу на экране осциллографа рассмотрим на примере ряда синусоидальных сигналов, подаваемых на входы Х и У (рис.3). Мы будем последовательно рассматривать положение луча на экране осциллографа в различные моменты времени (рис. 3а); различные моменты времени обозначены цифрами 1-9. В данном случае сигналы имеют одинаковую фазу: начальный момент времени t₁ напряжение V_x=V_y=0. Следовательно, в момент времени t₁ электронный луч попадает в центр экрана (точка 1, рис.3а). Смещение луча вправо или влево осуществляется под действием переменного напряжения V_x(t), изменяющегося с частотой f_x; смещение луча вверх или вниз осуществляется под действием переменного напряжения V_y изменяющегося с частотой f_y; в данном случае частоты f_x и f_y равны друг другу (рис.3а). Предполагается, что если напряжение V_x положительно, то луч смещается к правой пластине, если напряжение V_x отрицательно (например в моменты времени 5,6), то луч смещается влево, если напряжение V_y положительно (например в моменты 2,3), то электронный луч смещается вверх, если напряжение V_y отрицательно (например в моменты времени 5,6), то луч смещается вниз.

В момент времени t₂ за счет напряжения V_x луч смещается вправо, за счет V_y - вверх, поэтому в целом луч перемещается на экране по прямой в первой координатной четверти. В момент времени t₃ луч отклоняется по прямой 1-2-3 на максимальное расстояние. К моменту времени t₄ за счет уменьшения напряжения V_x, V_y луч смещается одновременно влево и вниз, наконец, в момент времени t₄ луч опять находится в центре экрана. В дальнейшем, в момент времени t₅ напряжение V_x и V_y имеют отрицательный знак, поэтому луч сильно смещен одновременно влево и вниз. В момент времени t₇ луч опять находится в центре экрана.

Таким образом, при одинаковой частоте сигналов и одинаковых фазах, фигура Лиссажу представляет собой прямую линию, наклон которой зависит только от соотношения амплитуд сигналов, подаваемых на входы Х и У. В частности, увеличение амплитуда сигнала, подаваемого на вход Х (напряжение V_x), приведет к уменьшению угла a между осью Х и прямой линией фигуры Лиссажу (рис.4,а, пунктирная линия).

Подадим на вход осциллографа (“вход Х”) сигнал частотой f_x; напряжение V_x (t) изображено на рис.3б; на “вход У” подадим сигнал, частота f_y которого в два раза больше, чем f_x, то есть f_y=2f_x. Начальные фазы сигналов в данном случае совпадают и равны 0: при начальном моменте времени t=0 напряжения V_x=V_y=0.Построение фигуры Лиссажу, получаемой на экране осциллографа, можно произвести с учетом напряжений V_x (t) и V_y(t) в моменты времени t₁, t₂ и т.д. В данном случае на экране получается устойчивая фигура Лиссажу в форме “восьмерки” (рис.3б); стрелками указано движение электронного луча по экрану в различные моменты времени.

Изменение фазы сравниваемых сигналов приводит к изменению формы фигуры Лиссажу. Например, на входы Х и У подаются сигналы V_x(t) и V_y(t) с разными начальными фазами: в момент времени t₁ напряжение V_x=0, а напряжение V_y>0. Частоты сигналов f_x и f_y одинаковы. Построение фигуры Лиссажу по принципу, описанному выше, показывает, что на экране виден наклонный эллипс (рис.3а).

Сравнивая рис.3а и 3в, получаем, что при одинаковых частотах f_x =f_y фигура Лиссажу может быть как прямой линией, так и эллипсом.

Форма фигуры Лиссажу может быть описана аналитически. Пусть на входы Х и У подается синусоидальное напряжение, для простоты одинаковой частоты f₀. Тогда координаты точки отклонения луча на экране (с учетом выражения (1)) будет описываться формулами:

;

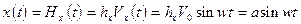(2)

; ; ,

где х(t) и у(t) - отклонение луча по горизонтали и вертикали в момент времени t; а и b - амплитудные значения отклонений; j₀ - сдвиг фаз между исследуемыми сигналами.

Траектория луча на экране осциллографа описывается зависимостью у(х), то есть для получения зависимости у(х) необходимо из уравнений (2) исключить время t. Для этого делаем следующие преобразования:

;

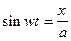(3)

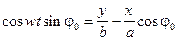или . (4)

Возведем выражение (3) в квадрат и умножим на величину sin²j₀, выражение (4) возведем в квадрат. В результате преобразований получим:

;

.

Сложим, получим выражения:

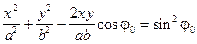. (5)

Выражение (5) описывает геометрическую фигуру - эллипс. Ориентировка эллипса относительно осей Х и У зависит от значения j₀.

Для j₀ = 0 или j₀ = 180 уравнение приобретает вид:

, ;

, .

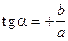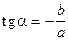В этом случае на экране появляется прямая линия, аналогичная рассмотренной выше (см. рис. 3а).

В случае неравенства частот и фаз на экране осциллографа возникают более сложные фигуры Лиссажу. Фигуры на экране будут неподвижными, если сравниваемые частоты относятся как целые числа и фаза не изменяется.

Для определения отношения частот придерживаются следующего правила.

При измерении частоты неизвестного сигнала частоту эталонного генератора изменяют до тех пор, пока на экране не возникнет одна из фигур Лиссажу, возможно, более простой формы. Ее мысленно пересекают линиями ХХ и УУ, параллельными условным осям Х и У, и подсчитывают число пересечений каждой из линий ХХ и УУ с фигурой Лиссажу, видимой на экране осциллографа. Математический анализ показывает, что для соотношения частот справедливо следующее выражение: или 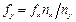, где f_y, f_x - частоты сигналов, подаваемых на пластины Х и У соответственно; nx, ny - число пересечений линий ХХ и УУ с фигурой Лиссажу.

В частности, для случая (рис.3б) отношение 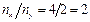, т. е. ; справедливость расчета подтверждается построением рис. 3б. Аналогично можно доказать, что для фигур, изображенных на рис. 4. г, д отличаются значениями разности фаз между напряжениями сигналов, подаваемых на входы Х и У. Таким образом, подавая на пластины У сигналы эталонной f₀ (известной) частоты, а на пластины Х - сигнал неизвестной частоты f_x, можно, определив отношение 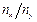, найти значение неизвестной частоты по формуле (6).

При помощи фигур Лиссажу можно измерять разность фаз между двумя периодическими сигналами. Рассмотрим метод измерения разности фаз на примере двух сигналов одинаковой частоты, подаваемых на входы Х и У.

Видно, что сигналы, подаваемые на входы Х и У, представляют собой гармонические колебания и, следовательно, описываются известным уравнением:

,

где U₀ - максимальное значение напряжения - амплитуда колебания; w - круговая (циклическая) частота, равная w=2pf; j₀ - начальная фаза колебаний в момент времени t=0; (wt+j₀) - фаза колебаний в момент времени t. Поскольку значение синуса может изменяться от -1 до +1, то напряжение сигнала изменяется со временем от -U₀ до +U₀.

Для нашего конкретного случая имеем:

;

.

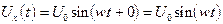Обратим внимание на то, что в любой момент времени фазы сигналов U_x и U_y одинаковы; в связи с этим говорят, что разность между сигналами равна нулю, сигналы изменяются с одинаковой фазой.

Для другого случая имеем

U_x(t) = U₀*sin (wt+0) = U₀*sin (wt);

U_y(t) = U₀*sin (wt+p/2),

то есть разность фаз между сигналами, очевидно, равна p/2.

Для третьегос лучая, имеем

U_x(t) = U₀*sin (wt+0) = U₀*sin (wt);

U_y(t) = U₀*sin (wt+p/4),

то есть для данного случая разность фаз между сигналами равна p/4.

Фигуры Лиссажу, получаемые на экранах осциллографов для различных случаев, представлены на рис. 5. Если сигналы одинаковой частоты изменяются в фазе (разность фаз равна нулю), то на экране будет наклонная линия (рис. 5, а); если сдвиг фаз равен p/2, на экране будет круг (при одинаковых амплитудах сигналов); если разность фаз находится в пределах 0<j₀<p/2, то на экране осциллографа будет фигура Лиссажу в виде наклонных эллипсов (рис. 5, в).

Исследование фигуры Лиссажу позволяет определить разность фаз между сигналами. Считаем, что на входы Х и У поданы сигналы

U_x = U₀*sin wt, U_y = U₀*sin(wt+j₀); разность фаз между ними равна j₀. Данные напряжения вызовут смещение луча по горизонтали и вертикали экрана с учетом соотношения (1)

по оси У: x(t) = H_x = h_x*U₀*sin wt;

по оси Х: y(t) = H_y = h_y*U₀*sin (wt+j₀). (7)

В зависимости от разности фаз фигура Лиссажу пересекает ось Х в одной или нескольких точках. Определим точку пересечения фигуры Лиссажу с осью абсцисс (точка М); из рис. 6.5, в видно, что координаты точки М: У=0, Х=Х₁. Значения Х₁ может быть определено на экране экспериментально.

Из уравнения (7) следует: y = 0 = h_y*U*sin (wt+j₀),

то есть координата У = 0 при значении аргумента wt = -j₀. При данном значении аргумента

x = x₁(j₀) = h_x*U₀*sin (-j₀) = h_x*U₀*sin j₀.

С другой стороны, максимальное значение Х₀ (см. рис.5,в), которое также может быть определено экспериментально, равно (из уравнения (7)): x₀ = h_x*U₀.

Следовательно, отношение х₁ / х₀ = sin j₀ определяет значение j₀, то есть

x₁ / x₀ = (h_x*U₀*sin j₀) / (h_x*U₀) = sin j₀,

или разность фаз между сигналами равна

j₀ = arcsin (x₁ / x₀) (8)

Таким образом, определяя в ходе эксперимента значения Х₁ и Х₂, вычисляя отношение Х₁ / Х₀, можно с учетом уравнения (8) определить разность фаз между сигналами, подаваемыми на входы Х и У. Именно это осуществляется на практике.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Дата добавления: 2015-06-04