Порядок виконання роботи. Тут m - маса молекули ідеального газу; k - стала Больцмана;

.

Тут m - маса молекули ідеального газу; k - стала Больцмана;

Т - абсолютна температура.

Розподіл за компонентами швидкостей має вигляд:

(4)

Після інтегрування по усіх значеннях змінних θ та φ, можна знайти кількість молекул в одиниці об'єму, швидкості яких знаходяться в інтервалі від u до u + du:

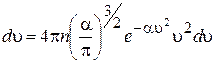. (5)

Вираз (5) називають розподілом Максвелла.

Крива розподілу Максвелла прямує до нуля при значенні швидкості руху частинок u= 0 та u= . У розподілі Максвелла є максимум, відповідний швидкості 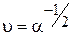, тобто .

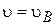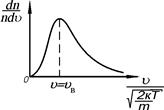
Рис. 1

Експериментальна перевірка розподілення молекул за швидкостями являє собою одну з головніших задач молекулярної фізики. Існують кілька методів, прямих та непрямих, які доводять справедливість цього закону.

У роботі для визначення виду функції розподілу за швидкостями використовується метод стримуючого потенціалу.

Відомо, що електронний газ, який створюється у просторі між катодом та керувальною сіткою електронної лампи внаслідок термоелектронної емісії, підкорюється статистиці Максвелла. Електронний газ має температуру катода. У багато електродній лампі типу пентода внаслідок її конструктивних особливостей електронна хмара має осьову симетрію. У цьому випадку для опису статистичних властивостей електронного газу варто використати формулу (3).

Якщоелектрони, що вилітають з катоду, примусити проходити крізь стримуюче електричне поле, то при деякій різниці потенціалів U ₃ подолати вплив поля можуть лише ті електрони, у яких радіальнаскладова швидкості відповідає умові:

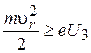, (6)

де е – заряд електрону; u – радіальна складова швидкості електрону.

Реєструючи кількість електронів, що подолали стримуюче поле, можна отримати криву розподілу Максвелла.

Покажемо, що це дійсно так. Для цього знайдемо кількість електронів, що пролітають крізь стримуюче поле за одиницю часу.

Спочатку, користуючись формулою (3), визначимо кількість електронів, які мають значення радіальної складової швидкості у діапазоні від 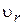до :

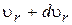. (7)

Кількість електронів , швидкості яких знаходяться у зазначеному діапазоні, які проходять крізь поверхню циліндричного електрода за одиницю часу, буде дорівнювати , тобто

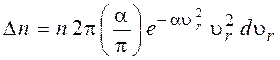
Кількість електронів n, що пролітають крізь простір із запираючим потенціалом U₃, буде визначатися кількістю електронів, швидкість яких перевищує ;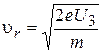

. (9)

Вираз (9) з точністю до постійної співпадає з розподілом Максвелла (див. формулу 5).

Для того щоб зафіксувати 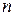, необхідно між анодом та останньою сіткою лампи створити таке прискорююче поле, різниця потенціалів у якому забезпечувала б проходження струму насичення в анодному колі.

Змінюючи величину стримуючої різниці потенціалів, можна отримати функцію 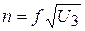похідна якої по , є розподілом Максвелла.

Опис експериментальної установки.

У роботі розподіл Максвелла перевіряється на установці, схема якої наведена на рис.2.

В якості електронної лампи застосовується пентод 6П9.

Електронна хмара створюється у просторі катод - управляюча сітка, потенціали яких практично рівні. Між сітками 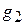та 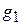за допомогою випрямляча ВС-24М створюється запираюче поле. Вели¶чина 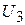може змінюватися від 0 до 30 В. Вольтметр виміряє .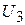

Рис.2

Електрони, які пролітають простір із затримуючим полем, проходять після цього прискорююче поле між анодом та останньою сіткою. Прискорююча різниця потенціалів забезпечується роботою випрямляча ВУП-2. Різниця потенціалів між анодом та сіткою підбирається такою, щоб забезпечити в анодному колі струм насичення, тобто усі електрони, швидкість яких більше 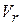, попадають на анод. Анодний струм реєструється мікроамперметром типу М-95. Між сітками 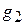та 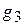увімкнено опір R₂ =5 МОм.

Описана схема включення дозволяє звести до мінімуму вплив зміни різниці потенціалів між сітками та на густину електронів у прикатодному просторі, що суттєво при перевірці закону розподілу за швидкостями.

Крім того, при такій схемі включення пентоду взаємний вплив джерел струму в анодному колі, де створюється стримуюча різниця потенціалів, будє мінімальним.

1. Зібрати експериментальну установку згідно з рис.2. За допомогою відповідної ручки управління випрямляча ВУП-2 встановити напругу, яка забезпечує проходження струму в анодному колі.

При зміні величини анодного струму перемикач прибору М-95 повинен бути виставлений у положення, при якому номінальний показник приладу дорівнює 10мкА.

2. За допомогою ручки на передній панелі випрямляча ВС-24М змінити величину стримуючої напруги від 0 до 10 В. Величину 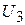від 0 до 1,5 В змінюють через 0,3 В; від 1,5 до 3 В – через 0,5В; від 3 до 10 В – через 1 В.

Для кожного значення стримуючого потенціалу записується струм. Подібного роду заміри зробити три рази.

3. Виміряні результати занести до табл.1 та визначити середнє значення величини анодного струму I_a, побудувати графік залежності (10) (див. рис.3).

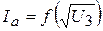(10)

Рис.3

Таблиця 1

U3, В		0,8	0,5	0,81	1,0	1,5	2,0	2,5	3,0	4,0	5,0	6,0	7,0
Ia, мА

4. Графічно про диференціювати функцію (10) та побудувати графік функції (11)на міліметрівці (див. рис. 4).

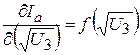(11)

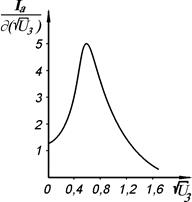
Рис. 4

Для побудови графіка на рис. 3 і 4 у кожній точці кривої провести дотичну та визначити тангенс кута нахилу кривої, створеного дотичною та горизонтальною лініями - це і буде .

Відповідно до теорії, похідна

з точністю до постійної буде збігатися з формулою розподілу Максвелла.

Для перевірки цього ствердження необхідно порівняти отриману криву з теоретичною кривою розподілу Максвелла, графік якої приведений на рис.1.

При цьому необхідно враховувати, що порівнювані криві побудовані в різних масштабах. Тому необхідно зробити норміровку змінних для отриманої функції як за віссю абсцис, так і за віссю ординат.

Значення за віссю абсцис норміруються до одиниці для того значення , де функція має максимум.

Значення функції (11) за віссю ординат норміруються до значення 0,84 у точці екстремуму.

Вибір такої норміровки для (11) обумовлений тим, що в літературі звичайно наводяться числові дані для функції розподілу Максвелла, записаної у вигляді:

.

Якщо швидкість вимірювати у відносних одиницях 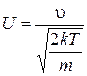, то при U = 1 - n приймає значення, рівне 0,84. Результати занести в таблицю.

Дата добавления: 2015-06-04