Критерий устойчивости для системы с постоянными объемом и энтропией

Принимая во внимание соотношение 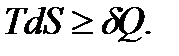и первое начало термодинамики, можно написать:

(1)

При постоянстве энтропии и объема это дает

(2)

т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением внутренней энергии. Следовательно, устойчивым является состояние при минимуме внутренней энергии.

Критерий устойчивости для системы с постоянными давлением и энтропией. В этом случае условие (1) имеет вид

(3)

т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением энтальпии Следовательно, устойчивым является состояние при минимуме энтальпии.

Критерий устойчивости для системы с постоянными объемом и температурой. При и 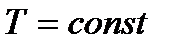неравенство (1) записывается в виде

(4)

т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением свободной энергии 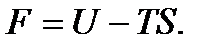Следовательно, устойчивым является лишь состояние при минимуме свободной энергии.

Критерий устойчивости для системы с постоянными температурой и давлением. С помощью выражения 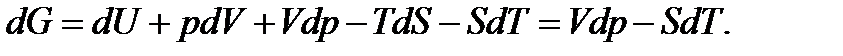для термодинамического потенциала неравенство (1) преобразуется к виду

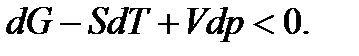(5)

При постоянных температуре и давлении дифференциалы и (5) сводятся к неравенству

(6)

т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением термодинамического потенциала. Следовательно, устойчивым является состояние при минимуме термодинамического потенциала Гиббса.

Принцип Ле-Шателье – Брауна

Рассмотрим принцип, сформули­рованный французским ученым Ле-Шателье (1850—1936) в 1884 г. и, в расширенном виде, немецким физиком Брауном (185О—1918) в 1887 г. Этот принцип позволяет предвидеть направление течения процесса в системе, когда она выведена внешним воздействием из состояния устойчивого равновесия. Принцип Ле-Шателье — Брауна не является столь всеобъемлющим, как второе начало термодинамики. В частности, он не позволяет высказывать никаких коли­чественных заключений о поведении системы. Необходимым усло­вием применимости принципа Ле-Шателье — Брауна является наличие устойчивости равновесия, из которого система выводится внешним воздействием. Он неприменим к процессам, переводящим систему в более устойчивое состояние, например, к взрывам. Прин­цип Ле-Шателье — Брауна был сформулирован как обобщение зна­менитого и всем хорошо известного электродинамического правила ленца (1804—1865), определяющего направление индукционного тока. Он гласит:

Если система находимся в устойчивом равновесии, то всякий про­цесс, вызванный в ней внешним воздействием или другим первичным процессом, всегда бывает направлен таким образом, что он стремится уничтожишь изменения, произведенные внешним воздействием или первичным процессом.

Ле-Шателье и Браун применяли главным образом индуктивный метод, рассмотрев большое число примеров, которые, по их мнению, являются частными случаями сформулированного ими общего прави­ла. Данная ими формулировка была, однако, столь туманной, что не допускала в каждом конкретном случае однозначного применения правила. Неопределенность можно устранить и получить точные математические формулы, выражающие принцип Ле-Шателье —Брауна, если к рассматриваемой проблеме привлечь критерии устойчивости термодинамического равновесия, сформулированные в предыдущем параграфе.

Дата добавления: 2015-06-04