Вторая теорема Карно. Неравенство Клаузиуса. Энтропия термодинамический системы. Закон возрастания энтропии

2-ая теорема Карно: Если две тепловые машины имеют общий нагреватель и холодильник и одна обратимая, а другая необратимая, то КПД обратимой больше необратимой

Отношение количества теплоты, подведенной к системе, к температуре, при которой это происходит, называется приведенной теплотой. Таким образом, - приведенная теплота, передаваемая системе. - приведенная теплота в 1 процессе. - приведенная теплота во II процессе. На участках 2-3 и 4-1 Q=0. Следовательно, это вся теплота охватывающая цикл Карно. Таким образом, для обратимого цикла Карно (9.26)

Так как любой замкнутый цикл можно представить как сумму бесконечного числа циклов Карно, то для любого замкнутого обратимого цикла выражение (9.26) будет справедливо и его можно записать в следующем виде 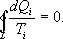(9.27)

Последнее соотношение носит название равенства Клаузиуса.

Необратимый цикл Карно.В этом случае

И все равенства превращаются в неравенства

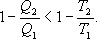
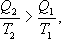
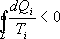(9.28)

Уравнение (9.28) называется неравенством Клаузиуса.

Объединяя (9.27) и (9.28), получим (9.29)

Таким образом, сумма приведенных теплот любого цикла равна нулю (обратимый процесс) или меньше нуля (необратимый процесс).

Из теоремы Клаузиуса следует, что приведенная теплота подобно энергии (потенциальной, внутренней) является функцией состояния (не зависит от пути перехода и зависит только от состояния системы). Независимость интеграла 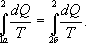от пути перехода означает, что этот интеграл выражает собой изменение некоторой функции состояния системы, она называется энтропия и обозначается буквой S. Изменение энтропии системы, очевидно, равно (9.30)

Мы говорим только об изменении энтропии (подобно изменению потенциальной энергии, для которой не важно где начало отсчета). Из уравнения (9.30) вытекает основное количественное выражение второго начала термодинамики

21. Статистический смысл энтропии. Понятие о статистическом весе макросостояния термодинамической системы.

Количество различных микросостояний, реализующих данное макросостояние системы, называется статистическим весом или термодинамической вероятностью макросостояния.

Все микросостояния системы равновероятны, а вероятность (математическая) макросостояния определяется ее статистическим весом. Анализ значений статистических весов различных макросостояний показывает, что в равновесном состоянии статистический вес максимален. Это означает, что все макроскопические процессы обладают односторонней направленностью. Переход между двумя макроскопическими состояниями возможен только в том случае, если конечное состояние является более вероятным, чем начальное. В этом заключается механизм необратимости тепловых процессов, которая проявляется в стремлении всех макроскопических тел перейти в равновесное состояние. С другой стороны, статистика не исключает самопроизвольных переходов в неравновесные состояния, просто эти переходы маловероятны (статистические флуктуации).

Получим выражение для статистического веса макросостояния. Пусть в системе имеется N частиц, а все фазовое пространство (область возможных значений координат и импульсов) разбито на m ячеек. Рассчитаем статистический вес состояния, при котором: в 1^ой ячейке находится N₁ частиц; во 2^ой ячейке – N₂ частиц и т.д.; в m^ой ячейке - N_m частиц. Для этого достаточно рассчитать число возможных перестановок частиц между ячейкам (они не изменяют числа частиц в ячейках). Это можно сделать, если из общего числа перестановок N частиц N! исключить перестановки в пределах каждой ячейки N_i! (они ничего не изменяют).

.

Если в системе создать искусственно неравновесное состояние, то в подавляющем большинстве случаев система самопроизвольно будет переходить в состояние с большей вероятностью. С другой стороны, согласно термодинамике, все самопроизвольные процессы в замкнутой системе сопровождаются возрастанием энтропии. Поэтому следует ожидать, что между энтропией системы S в каждом состоянии и вероятностью W того же состояния должна существовать однозначная связь. Эта связь была установлена Больцманом (формула Больцмана):

,

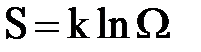где k – постоянная Больцмана.

Последнее соотношение можно рассматривать как определение энтропии. При таком понимании энтропии закон ее возрастания утрачивает свою абсолютность и становится статистическим законом. Энтропия замкнутой системы может не только возрастать, но и убывать. Это можно трактовать следующим образом: если система находится в неравновесном состоянии, то переход ее в более вероятное состояние будет происходить в подавляющем большинстве случаев, переходы же в менее вероятные состояния (с меньшей энтропией) настолько маловероятные, что практически не имеют никакого значения. Тогда закон возрастания энтропии оправдывается на практике с абсолютной достоверностью.

Дата добавления: 2015-06-04