С учетом (2) формула (1) примет вид

A

dQx

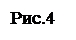l l

Согласно принципу суперпозиции электрических полей, потенциал электрического поля, создаваемого заряженным стержнем в точке А, найдем интегрированием этого выражения:

.

Выполним интегрирование:

.

Подставим числовые значения физических величин в СИ (τ = 10 · 10^-9 Кл/м, 1/(4πε₀) = 9 · 10⁹ м/Ф) и произведем вычисления:

.

Пример 5. На пластинах плоского конденсатора находится заряд Q = 10 нКл. Площадь S каждой пластины конденсатора равна 100 см², диэлектрик – воздух. Определить силу F, с которой притягиваются пластины. Поле между пластинами считать однородным.

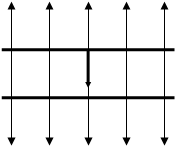
Р е ш е н и е. Заряд Q одной пластины находится в поле напряженностью Е, созданном зарядом другой пластины конденсатора. Следовательно, на первый заряд действует сила (рис.5)

F = QE. (1)

Так как

E Е = σ / (2ε₀) = Q / (2ε₀S),

-Q - - - - где σ – поверхностная плотность заряда, то

формула (1) примет вид

F F = Q² / (2ε₀S).

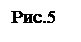Q + + + + Произведем вычисления:

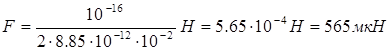
Пример 6. Электрическое поле создано длинным цилиндром радиусом R = 1 см, равномерно заряженным с линейной плотностью τ = 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии а₁ = 0.5 см и а₂ = 2 см от поверхности цилиндра, в средней его части.

Р е ш е н и е. Для определения разности потенциалов воспользуемся соот- ношением между напряженностью поля и изменением потенциала: E = - grad φ. Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде

.

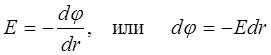Интегрируя это выражение, найдем разность потенциалов двух точек, отстоящих на расстояние r₁ и r₂ от оси цилиндра:

. (1)

Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой напряжен-

ности поля, создаваемого бесконечно длинным цилиндром:

.

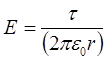Подставив выражение Е в (1), получим

Произведем вычисления, учитывая, что величины r₁ и r₂, входящие в формулу (2) в виде отношения, можно выразить в сантиметрах (r₁ = R + a₁ = 1.5 см, r₂ = R + a₂ = 3 см):

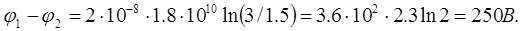
Пример 7. Конденсатор емкостью С₁ = 3 мкФ был заряжен до разноси потенциалов U₁ = 40 В. После отключения от источника тока конденсатор соединили параллельно с другим незаряженным конденсатором емкостью С₂ = 5 мкФ. Какая энергия W΄ израсходуется на образование искры в момент присоединения второго конденсатора?

Р е ш е н и е. Энергия, израсходованная на образование искры,

(1)

где W₁ – энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора; W₂ – энергия, которую имеет батарея, составленная из двух конденсаторов.

Энергия заряженного конденсатора определяется по формуле

(2)

где С – емкость конденсатора или батареи конденсаторов.

Выразив в формуле (1) энергии W₁ и W₂ по формуле (2) и, приняв во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим

(3)

где U₂ – разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов U₂ следующим образом:

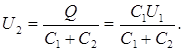(4)

Подставив выражение U₂ в (3), найдем

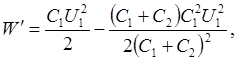или

Произведем вычисления:

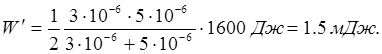
Пример 8. Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Δ t = 2 с по линейному закону от I ₀ = 0 до I = 6 А. Определить теплоту Q₁, выделившуюся в этом проводнике за первую секунду, и Q₂ – за вторую, а также найти отношение Q₂/Q₁.

Р е ш е н и е. Закон Джоуля-Ленца в виде Q = I ² Rt справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого интервала времени и записывается в виде

dQ = I ² Rdt (1)

Здесь сила тока I является некоторой функцией времени.

В данном случае

I = kt, (2)

где k – коэффициент пропорциональности, характеризующий скорость изменения силы тока:

Рис. 6

.

dQ = k ² Rt ² dt. (3)

Для определения теплоты, выделившейся за конечный интервал времени Δt, выражение (3) надо проинтегрировать в пределах от t₁ до t₂:

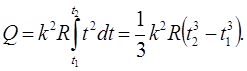
Произведем вычисления:

;

.

Следовательно,

,

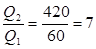т.е. за вторую секунду выделится теплоты в семь раз больше, чем за первую.

Дата добавления: 2015-06-04