Изгиб балки

При изгибе стержня, схема нагружения которого дана на рис. 4а, требуется определить внутренние силовые факторы и напряжения во всех его поперечных сечениях и построить их эпюры вдоль оси бруса. Исходя из анализа построенных эпюр напряжений с учётом условия прочности стержня, определить

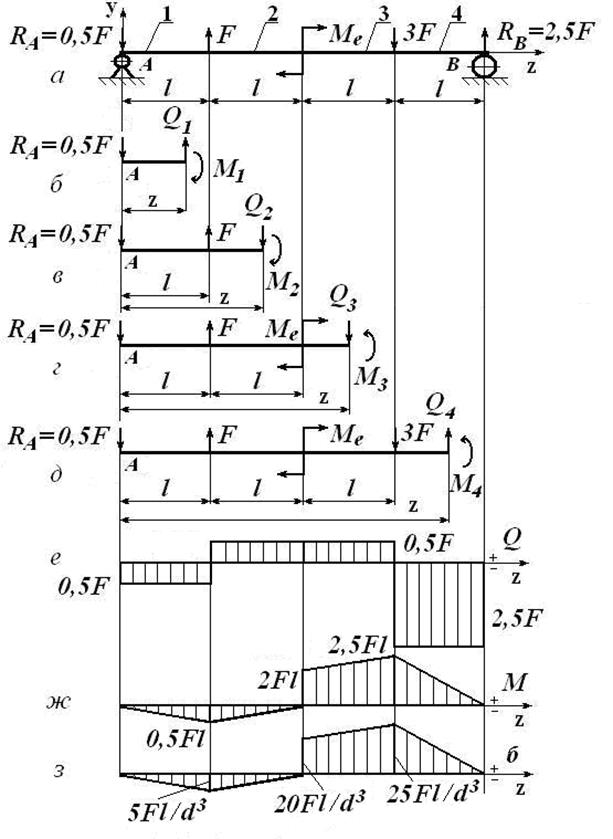
Рис. 4. Расчётная схема и эпюры внутренних силовых

факторов и напряжений при изгибе стержня

минимально допустимое значение диаметра 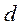его круглых сплошных сечений, если известно, что изгибающий момент 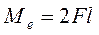, сила 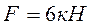, длина участка стержня 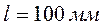, предел текучести материала стержня 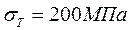, допускаемое значение коэффициента запаса прочности .

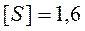Решение

1. Отбрасывая левую и правую опоры балки, заменяем их действие реакциям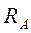и и 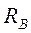(рис. 4а), значения которых находим из условий её равновесия [1]

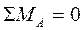или ,

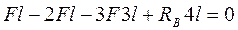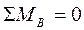или ,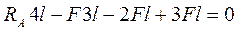

где 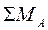и 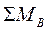- суммы всех моментов относительно, соответственно, точек А и В, действующих на балку. При этом моменты от нагрузок, поворачивающих балку относительно опоры против часовой стрелки берут со знаком «+», а по часовой стрелке – со знаком «-».

Решив полученные уравнения относительно реакций, получаем

,

.

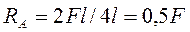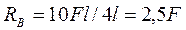Так как значения 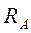и 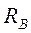получились положительными, то их предварительно произвольно выбранные направления оказались верными. В противном случае направления реакций в расчётной схеме меняют на противоположные.

Проверкой правильно найденных значений реакций опор является

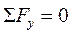или ,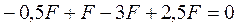

где 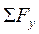- сумма проекций на ось 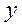всех сил, включая реакции, действующих на балку. При этом значения сил положительны, если их направление совпадает с направление оси 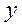, и отрицательны в противном случае.

2. Используя метод сечений, определяем внутренние силовые факторы во всех поперечных сечениях стержня с учётом следующих правил:

· поперечная сила 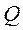в сечении балки равна сумме проекций на плоскость сечения всех внешних сил, лежащих по одну сторону от сечения, и считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа сверху вниз, и отрицательной, если наоборот (рис. 5);

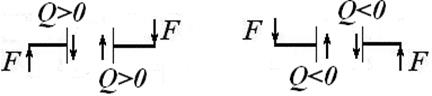
Рис. 5. Правило знаков для поперечных сил в сечениях стержня

· изгибающий момент 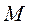в сечении балки равен сумме моментов относительно поперечной оси этого сечения всех внешних сил, расположенных по одну сторону от этого сечения, и считается положительным, если равнодействующий момент внешних сил слева от сечения направлен против часовой стрелки, а справа отсечения – по часовой стрелке, в противном случае он берётся отрицательным (рис. 6).

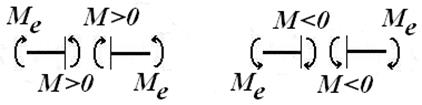
Рис. 6. Правило знаков для изгибающих моментов в сечениях стержня

Разбиваем стержень по длине вдоль оси 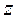на 4 характерных участка (поз. 1, 2, 3 и 4 на рис. 4а) с учётом точек приложения нагрузки.

Делаем поперечное сечение стержня в произвольном месте участка 1 с координатой 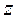(рис. 4б). Прикладываем в этом сечении поперечную силу 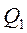и изгибающий момент 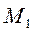и определяем их значения с учётом описанных правил

,

.

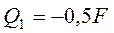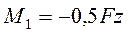При этом если значения поперечных сил одинаковы во всех сечениях участка 1 и равны 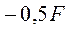, то значения моментов в сечениях этого участка увеличиваются прямо пропорционально росту координаты 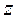и составляют в начале участка 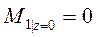, а в конце участка .

Повторяя для остальных участков стержня действия, аналогичные действиям, выполненным для участка 1, имеем:

· для участка 2 (рис. 4в)

,

,

,

;

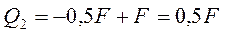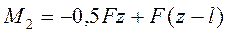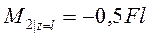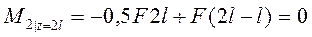· для участка 3 (рис. 4г)

,

,

,

;

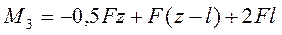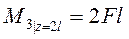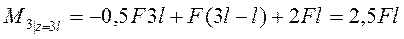· для участка 4 (рис. 4д)

,

,

,

.

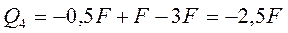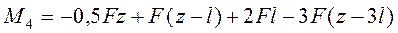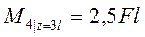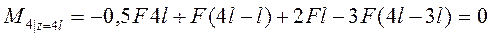С учётом полученных значений поперечных сил и изгибающих моментов во всех сечениях стержня на участках 1, 2, 3 и 4 их эпюры вдоль оси стержня имеют вид, представленный на рис. 4е и 4ж.

3. Согласно формуле (3) расчётные значения нормальных напряжений изгиба в сечениях стержня прямо пропорциональны значениям изгибающих моментов в этих сечениях на каждом из рассмотренных участков, следовательно

,

,

,

,

,

,

.

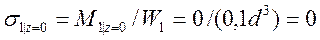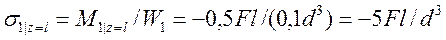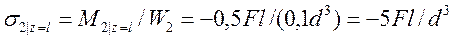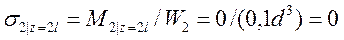
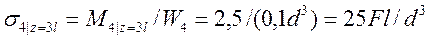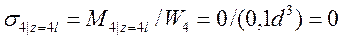Тогда эпюра напряжений 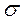вдоль оси 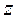стержня будет иметь вид, приведённый на рис. 4з.

4. Из анализа эпюры напряжений 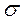(рис. 4з) определяем

.

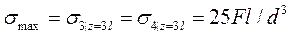Подставив полученное значение 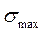в условие прочности стержня (6), имеем

.

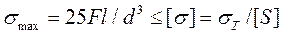Тогда минимальное минимально допустимое из условия прочности стержня значение диаметра 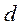сечения с учётом заданных численных значений силы 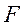, длины 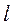, предела текучести материала стержня 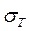и коэффициента запаса прочности 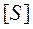можно рассчитать как

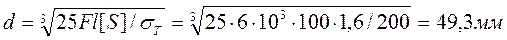
5. После определения величины 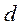, рассчитываем численные значения усилий и напряжений в поперечных сечениях стержня:

,

,

,

,

,

,

;

,

,

, .

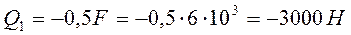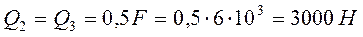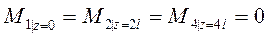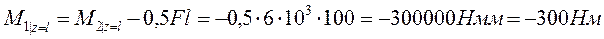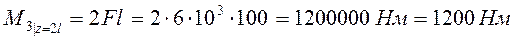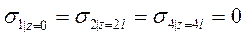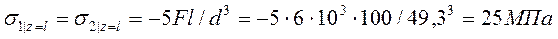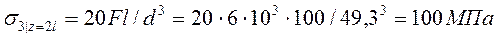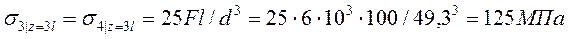Литература

1. Феодосьев В.И. Сопротивление материалов - М.: Изд-во МГТУ им. Н.Э. Баумана, 2010.

2. Практический курс сопротивления материалов / под ред. проф. И.В. Стасенко – М.: МГТУ им. А.Н. Косыгина, 2006.

Приложение

Домашнее задание по разделу «Сопротивление материалов»

дисциплины «Прикладная механика»

Задача №1

Определить внутренние силовые факторы, напряжения и линейные перемещения поперечных сечений бруса, схема нагружения которого дана на рис. П1. Построить их эпюры вдоль оси бруса и из условия его прочности при растяжении-сжатии определить минимально допустимые площади сечений А₁, А₂ и А₃, если известно, что сила F=20кН, расстояние l=100мм, предел текучести материала бруса σ_Т=240МПа, допускаемое значение коэффициента запаса прочности [S]=3.

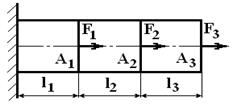
Рис. П1

Исходные данные по вариантам:

№ варианта	F1/F	F2/F	F3/F	l1/l	l2/l	l3/l	А1/A	А2/A	А3/A
		-1
	-1
		-1
			-1
			-2
	-1
		-1
			-1
	-2
		-1
	-1
			-2
		-1
			-2
	-3
	-3	-1
			-2
	-1	-3
			-3
	-2
Примечание: знак минус перед коэффициентом означает, что направление нагрузки противоположно направлению, указанному на рис. П1.

Задача №2

Определить внутренние силовые факторы, напряжения и угловые перемещения поперечных сечений бруса, схема нагружения которого дана на рис. П2. Построить их эпюры вдоль оси бруса и из условия его прочности при кручении определить минимально допустимые диаметры сечений d₁, d₂ и d₃, если известно, что крутящий момент T_e=1250Нм, расстояние l=200 мм, а допускаемое напряжение кручения материала бруса [τ]=50МПа.

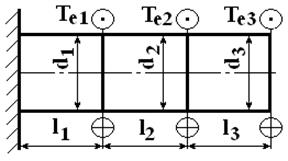
Рис. П2

Исходные данные по вариантам:

№ варианта	Te1/Te	Te2/Te	Te3/Te	l1/l	l2/l	l3/l	d1/d	d2/d	d3/d
			-1
	-2
			-2
	-1
			-2
		-1
	-1
		-2
			-1
			-1
	-2
			-2
	-1
Примечание: знак минус перед коэффициентом означает, что направление нагрузки противоположно направлению, указанному на рис. П2.

Задача №3

Определить внутренние силовые факторы и напряжения в поперечных сечениях балки, схема нагружения которой дана на рис. П3. Построить их эпюры вдоль оси балки и из условия её прочности определить минимально допустимый диаметр d постоянного по длине балки поперечного сечения, если известно, что сила F=2кН, расстояние l=100 мм, изгибающий момент M_e=kFl, а допускаемое напряжение изгиба материала бруса [σ]=100МПа.

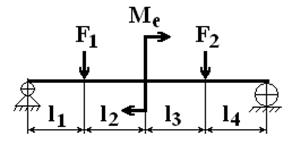
Рис. П3

Исходные данные по вариантам:

№ варианта	F1/F	F2/F	k	l1/l	l2/l	l3/l	l4/l
		-1	-1
	-1
	-1	-1	-2
		-2	-3
		-1
		-2	-2
	-2
	-2	-2
			-3
	-2		-1
		-1
	-1
	-1	-1	-2
		-1
		-2	-2
	-2
Примечание: знак минус перед коэффициентом означает, что направление нагрузки противоположно направлению, указанному на рис. П3.

Содержание

Введение …………………………………………………………………………… 3

1. Определение внутренних сил, напряжений и перемещений

в поперечных сечениях стержня и проверка его на прочность….………….. 4

2. Растяжение - сжатие стержня ………………………………….…………….. 7

3. Кручение круглого стержня ………………………………………….…..….. 13

4. Изгиб балки ……………………………………………………………….…... 19

Литература ………………………………………………………………….…….. 25

Приложение …………………………………………………………………….… 26

Дата добавления: 2015-06-04