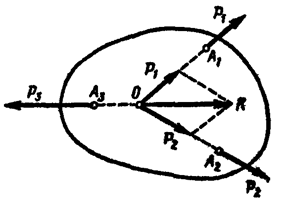
Линии действия трех непараллельных взаимно уравновешивающихся сил, лежащих в одной плоскости, пересекаются в одной точке.

Теорема о трех непараллельных силах

Аналитическая форма

Равнодействующая сходящихся сил (рис. 2.11) равна геометрической сумме этих сил:

.

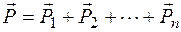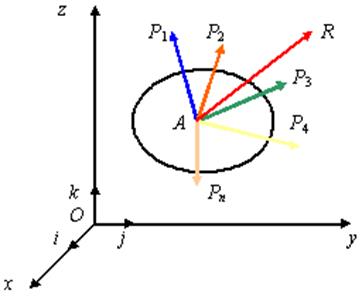
Рис. 2.11

Проекция равнодействующей на каждую из координатных осей равна алгебраической сумме проекций всех составляющих:

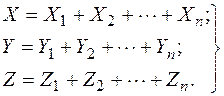(2.8)

здесь проекции сил вычисляются по формулам:

Формулам (3) можно придать вид

(2.9)

причем i= 1,2 ,…,n.

Вычислив проекции равнодействующей X, У и Z, найдем модуль и направление равнодействующей по формулам (2.8) и (2.9):

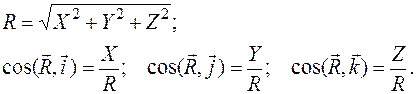
Если силы взаимно уравновешиваются, их равнодействующая равна нулю.

.

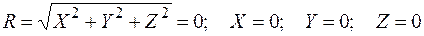Для сходящихся сил в пространстве имеем следующие три уравнения равновесия:

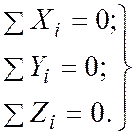(2.10)

Для сходящихся сил, расположенных в одной плоскости, получаем два уравнения равновесия:

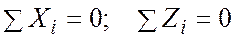. (2.11)

Задача 1. Груз M ₁ весом Р (рис. 1.2.1, а) подвешен на гибком не­растяжимом тросе ОМ ₁ отклоненном от вертикали на угол α, и удерживается в равновесии при помощи другого гибкого нерастя­жимого троса М ₁ АМ ₂, охватывающего идеальный блок А и несущего на свободном конце груз М ₂. Считая, что при равновесии участок троса М ₁ А горизонтален, определить величину Q веса груза М ₂ и на­тяжение троса ОМ ₁. Размерами груза М ₁ и весом тросов пренебречь.

Рис. 1.2.1

Аналитический способ.

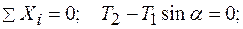
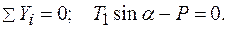
Отсюда находим

.

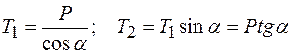Геометрический способ

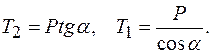
Задача 2. Однородный цилиндр А весом Р и радиусом r (рис. 1.2.2, а) опирается на гладкую поверхность цилиндра В радиусом R и удерживается в равновесии при помощи нити CD длиной l, расположенной в поперечной плоскости симметрии. Определить натяжение нити и реакцию цилиндрической поверхности.

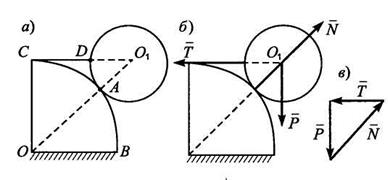
Рис. 1.2.2

Решение. Рассмотрим равновесие цилиндра А. На него действует сила Р, направленная вертикально вниз. Связями являются гладкая цилиндрическая поверхность В и нить CD. Освободимся от связей. Реакция N (рис. 1.2.2, б) цилиндрической поверхности направлена по общей нормали к цилиндрам и, следовательно, про­ходит через точку Ох. Реакция Т направлена по нити CD. Поскольку на цилиндр А действуют три силы, то на основании теоремы о трех силах их линии действия должны пересекаться в точке Ох. Следовательно, цилиндр А при равновесии займет такое положение, при котором нить CD будет являться продолжением его радиуса.

Построим силовой треугольник (рис. 1.2.2, в). Этот треугольник подобен Δ OO ₁ C. Из подобия треугольников имеем

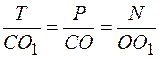или .

Отсюда находим

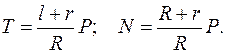
Задача 3. Груз весом Р = 60 кН подвешен при помощи каната, перекинутого через небольшой блок А и идущего к лебедке D. Определить усилия в стержнях АС и ВА крана. Углы, определяющие направления стержней и каната, заданы на рис. 1.2.6.

.

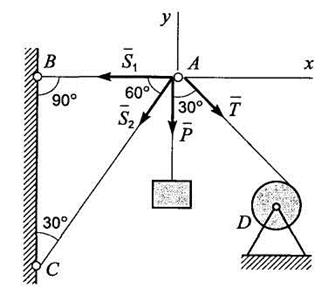
Рис. 1.2.6

Решение. Рассмотрим равновесие узла А крана, к которому приложены сила Р, реакции стержней АС и АВ и сила натяжения каната AD. Обозна­чим реакцию стержня АВ через S ₁ реакцию стержня АС через S ₂ и силу натяжения каната AD через Т.

Реакции стержней S ₁ и S ₂ направим вдоль этих стержней от узла А; сила Т направлена, очевидно, вдоль каната от А к D, так как канат растянут. Кроме того, Т=Р, так как при отсутствии трения в блоке натяжение каната, перекинутого через этот блок, во всех точках одинаково.

Так как узел А находится в равновесии под действием сил S ₁, S ₂, P, Т, то можно составить два уравнения равновесия этой системы сходящихся сил.

Выберем оси координат, как указано на рис. 1.2.6, найдем проекцию каждой силы на эти оси и составим два уравнения равновесия, приравнивая нулю сумму проекций всех сил на каждую из координатных осей:

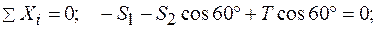
Из второго уравнения находим:

кН,

S ₂ =-129,1 кН.

Теперь из первого уравнения получаем:

кН.

Так как полученное значение силы S ₂ отрицательно, то сила S ₂ имеет направление, противоположное направлению, выбранному на рисунке, т.е. она направлена от С к А, и, следовательно, стержень АС сжат.

Задачу можно решить и геометрически, построив замкнутый многоугольник сил Т, Р, S ₁, S ₂ (рис. 1.2.7).

Рис. 1.2.7

Направления сил S ₁ и S ₂ найдем после того, как обойдем периметр построенного силового многоугольника, причем направ­ление этого обхода определяется направлением известных сил Р и Т.

Измерив стороны cd и da силового многоугольника выбранной единицей масштаба, найдем величину искомых сил S ₁ и S ₂. Так как углы между силами Т, Р, S ₁, S ₂ заданы, то можно найти углы силового многоугольника, а затем вычислить и длины двух неизвестных его сторон. В самом деле, из построения силового многоугольника следует, что

,

а потому

.

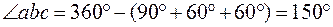Если соединим точки а и с, то треугольник аbс будет равно­бедренным, так как Р = Т, а потому

.

Отсюда следует, что

.

Применяя теперь к треугольнику adc теорему синусов, получим:

,

откуда

,

.

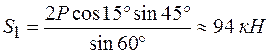Чтобы определить, будут ли стержни АВ и АС сжаты или растянуты (рис. 1.2.7), перенесем векторы S ₁ и S ₂ с силового многоугольника на стержни АВ и АС, тогда сила S ₂ будет направлена к узлу А, а сила S ₁, от узла А, а потому стержень АС сжат, а стержень АВ растянут.

Задача 4.. Жесткая рама (рис. 1.2.8) закреплена в точке А при помощи неподвижного цилиндрического шарнира, а в точке В опирается катками на гладкую наклонную плоскость, составляющую с горизонтом угол α = 30°. На горизонтальном участке CD рама находится под действием равномерно распределенной вертикаль­ной нагрузки интенсивности q = 5 кН/м. Определить реакции опор в точках А и В. если CD = 2 a = 2,1 м и ОК = b = .

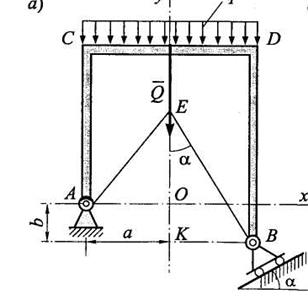
Рис. 1.2.8

Решение.

Рассмотрим теперь аналитический способ решения. Начало ко­ординат выберем в точке О, ось у направим по прямой ОЕ, а ось х — по прямой АО. Проектируя силы Q, R_A и R_B на оси х и у, получим следующие два уравнения равновесия:

Из первого уравнения находим

.

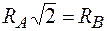Тогда из второго уравнения имеем

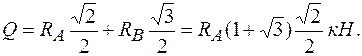
Отсюда

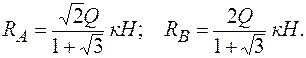
Задача 5. Груз весом G = 2 кН (рис. 1.2.15) удерживается краном, состоящим из двух невесомых стержней в шарнирах АВ и АС, прикрепленных к вертикальной стене и составляю­щих с ней углы α ₁ = 60° и α ₂ = 40°. В точке А подвешен блок, через который перекинут грузовой трос, идущий к блоку в точке D и составляющий со стеной угол α ₃ = 60°.

Весом троса и блока, а также размерами блока можно пренебречь. Определить усилия в стержнях.

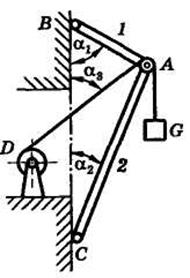
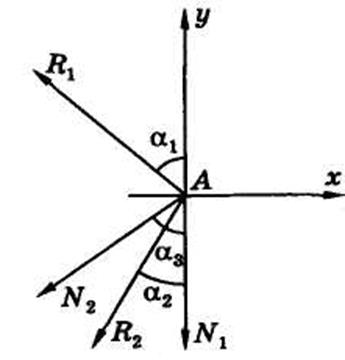
Реакции опорных стержней направлены, как извест­но, вдоль этих стержней. Направим их внутрь стержней, считая изначально стержни растянутыми.

Составим теперь уравнения равновесия как уравне­ния проекций сил на оси (для системы сходящихся сил), учитывая, что силы R ₁, R ₂ и N ₂ составляют углы α ₁, α ₂ и α ₃ с осью у.

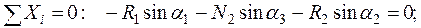
Отсюда, учитывая, что 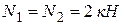, получаем

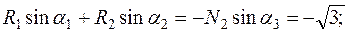
Решая эту систему уравнений, находим R ₁ = 0,611 кН, R ₂ = –3,52 кН. Знак «минус» у величины реакции R ₂ озна­чает, что она имеет направление, противоположное при­нятому, то есть стержень АС не растянут, а сжат.

Дата добавления: 2015-06-04