Контрольная работа 3 страница

Из условия задачи получаем:

1) ; ; ;

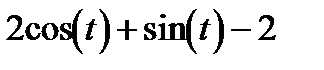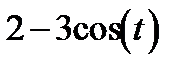2) ; ; ;

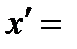
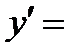
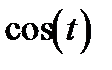Из (1) и (2):

3) ; ; .

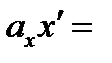
Интегралы от по промежутку от 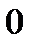до равны нулю, поэтому при вычислении 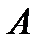эти части сразу отбрасываем. Тогда получится = = = = = = .

Ответ: .

Задача 12. Найти все значения корня.

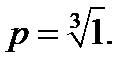
Решение:

Корни для комплексных чисел вычисляются по формуле 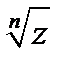= 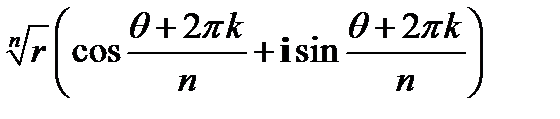, где k целое число больше или равно 0 и меньше n. Т.е. всегда имеется n корней; - главное значение аргумента z; r – модуль числа z.

Для z = 1 будет, и r = 1, тогда получим, при n = 3, три корня: , где ; ; .

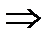
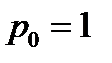Ответ: ; ; .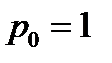

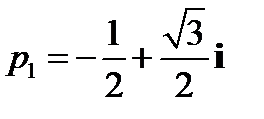Задача 13. Представить в алгебраической форме комплексные числа.

$p = Arch(-2).$

Решение:

= = = .

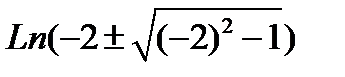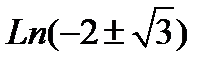Ответ: 1) , 2) .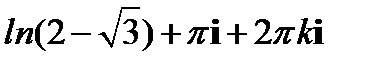

Задача 14. Вычертить область заданную неравенствами на комплексной плоскости.

1) , 2) .

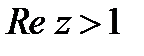Решение:

Пусть . Первое неравенство задает замкнутую область в виде круг радиуса 2, с центром в точке 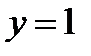. Второе неравенство задает открытую область в виде полуплоскости лежащей праве прямой 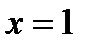. Оба неравенства задают пересечение этих областей .

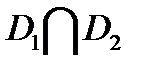Задача 15. Восстановить аналитическую в окрестности точки функцию по известной действительной или мнимой части и значению .

, .

Решение:

Для комплексных аналитических функций выполняются следующие условия: , 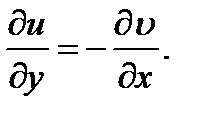Откуда получаем:

1) , где - функция зависящая только от y.

2) .

= ; = =

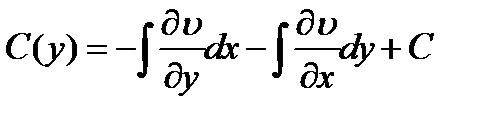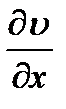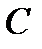= . Вычисляем действительную часть по формуле (1) подставляя полученные занчения:

= .

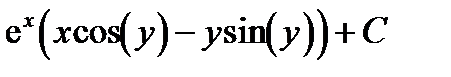Из условия найдем С: = = .

Ответ: = .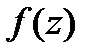

Задача 17. Данную функцию разложить в ряд Лорана в окрестности точки .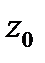

= .

Решение:

= = .

Разложим в ряд Тейлора 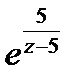по степеням : = = .

= = =

= = =

= . = = = .

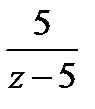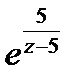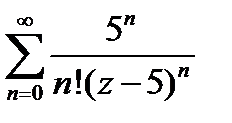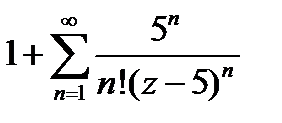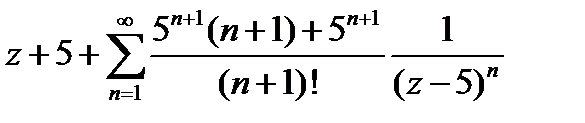Ответ: .

Задача 18. Вычислить интеграл.

.

Решение:

Подынтегральная функция имеет один полюс в точке . Поэтому =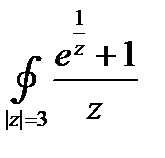

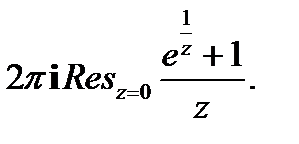= Вычислим вычет 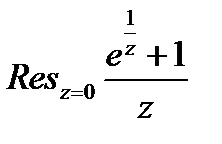как коэффициент ряда Лорана:

= = = = . = = .

= = .

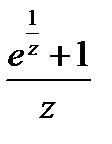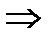
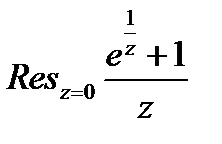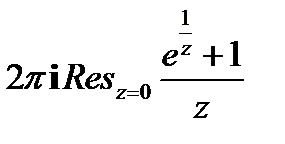Ответ: .

Задача 20. Вычислить интеграл с помощью комплексных чисел.

.

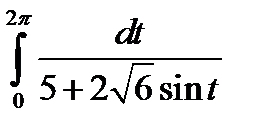Решение:

Выполним подстановку 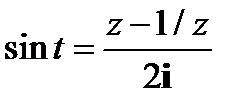, , тогда = =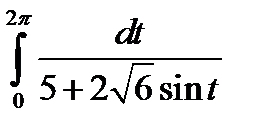

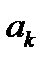= = , где - полюса подынтегральной функции лежащие внутри круга . Такими полюсами будут корни уравнения лежащие внутри круга . Корни равны: , . 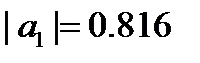- внутри круга, 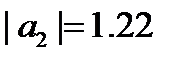- вне круга = = = = .

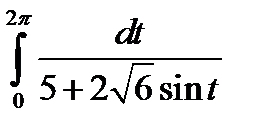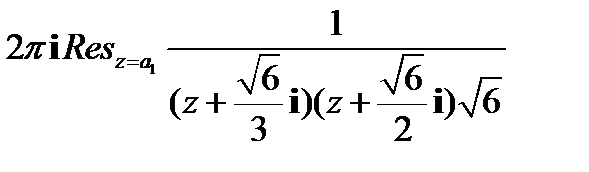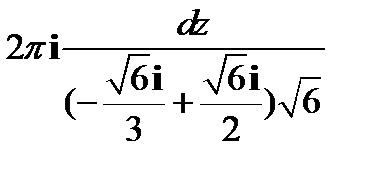Ответ: .

Задача 21. Вычислить интеграл с помощью вычетов.

.

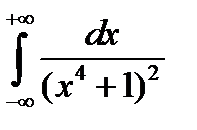Решение:

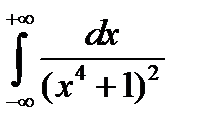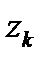= ,где -полюса подынтегральной функции лежащие в верхней полуплоскости. Корни Уравнения 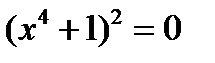равны:

= , = , = , = .

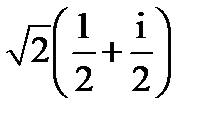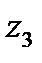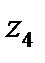Все корни имеют кратность два, следовательно, полюсы будут второго порядка. В верхней полуплоскости лежат и .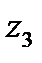

= .

Вычеты вычисляем по формуле .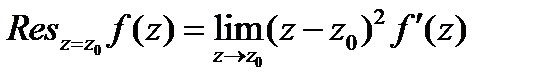

= , = =

= = .

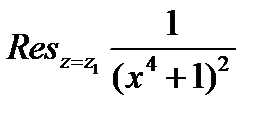Ответ: .

Дата добавления: 2015-06-04