Аксиома 5

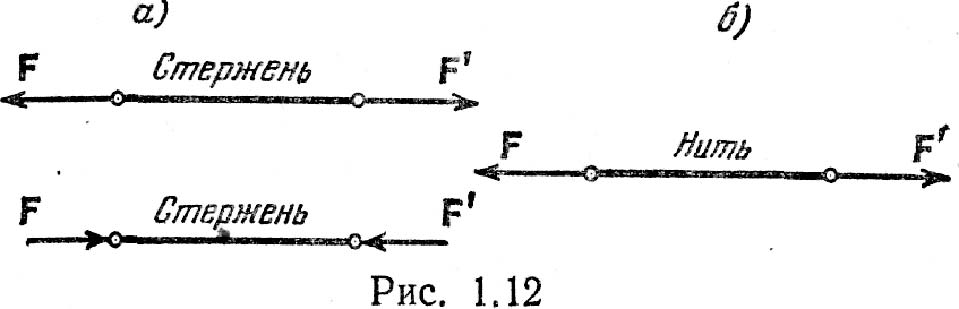
Аксиома 5. Равновесие деформируемого тела не нарушится, если жестко связать его точки и считать тело абсолютно твердым. Этой аксиомой пользуются в тех слу­чаях, когда речь идет о равновесии тел, ко­торые нельзя считать твердыми. Приложенные к таким телам внешние силы должны удов­летворять условиям равновесия твердого тела, однако для нетвердых тел эти условия являются лишь необходимыми, но не доста­точными. Например, для равновесия абсолютно твердого не­весомого стержня необходимо и достаточно, чтобы приложенные к концам стержня силы F и F' действовали по прямой, соединяю­щей его концы, были равны по модулю и нап­равлены в разные стороны. Эти же условия необходимы и для равновесия отрезка неве­сомой нити, но для нити они недостаточны— необходимо дополнительно потребовать, чтобы силы, действующие на нить, были растягивающими (рис. 1.12, б), в то время как для стержня они могут быть и сжимающими (рис. 1.12, а).

Рассмотрим случай эквивалент­ности нулю трех непараллельных сил, приложенных к твердому телу (рис. 1.13, а). Теорема о трех непараллельных силах. Если под действием трех сил тело находится в равновесии и линии действия двух сил пересекаются, то все силы лежат в одной плоскости, и их линии дей­ствия пересекаются в одной точке. Пусть на тело действует система трех сил F₁, F₃ и F₃, причем линии действия сил F₁ и F₂ пересекаются в точке А (рис. 1.13, а). Согласно следствию из аксиомы 2 силы F₁ и F₂ можно перенести в точку А (рис. 1.13, б), а по аксиоме 3 их можно за­менить одной силой R, при­чем (рис. 1.13, в) R=F₁+F₂. Таким образом, рассматриваемая система сил приведе­на к двум силам R и F₃ (рис. 1.13, в). По условиям теоремы тело находится в равновесии, следовательно, по аксиоме 1 силы R и F₃ должны иметь общую линию действия, но тогда линии действия всех трех сил должны пересекаться в одной точке.

Дата добавления: 2015-06-04