
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Статистическое регулирование стабильности технологического процесса
|
|
|
|
4.1. Теоретические основы
Цель статистического регулирования стабильности технологических процессов изготовления продукции - установление причин нарушения их нормального хода путем определения и анализа систематических и случайных погрешностей на основе ограниченного числа наблюдений, а затем и немедленное устранение причин этих нарушений.
Статистическое регулирование качества продукции заключается в корректировке параметров технологического процесса путем наладки (настройки) оборудования и машин на основе выборочного контроля изготавливаемой продукции в соответствии с оцениваемым признаком
/2-6/.
Особо важную роль здесь играют методы регулирования качества при операционном контроле, позволяющие своевременно устранить ошибки, уточнить объем выборки, внести корректировку в параметры технологического процесса, выявить необходимость ремонта (остановки) машин и оборудования.
Статистическое регулирование качества включает четыре операции: измерения контролируемых показателей; расчет статистических критериев; анализ причин отклонения показателей от допусков и корректировку работы машин и оборудования.
Технологические процессы характеризуются основными параметрами: технологической точностью и стабильностью.
Технологическую точность изучали в предыдущей работе. Технологи-ческая точность определяет степень соответствия поля рассеяния контро-лируемого параметра полю допуска и свидетельствует о том, насколько качество изготовляемой продукции соответствует требованиям стандартов. Однако технологическая точность характеризует процесс лишь в данный момент. Технологическая же стабильность определяется степенью сохраняемости заданных показателей качества продукции в некоторых пределах в течение времени.
В выборочном контроле стабильности технологического процесса используют мгновенные выборки, т.е. выборки малого объема из потока продукции, изготовленной в последний момент перед отбором. Промежуток времени отбора устанавливают весьма короткий. Поэтому одна из задач выборочного контроля - это анализ статистического ряда измерений и исключение грубых ошибок, которые возникают из-за различных случайных ошибок.
Если не исключить грубых погрешностей, то итоговый результат вычислений может существенно отличаться от действительного значения. Так, одна грубая ошибка в 20 измерениях значительно влияет на достоверность результата. Применяются различные методы исключения грубых погрешностей измерений.
Метод трех сигм базируется на положении, что при попадании погрешностей за пределы доверительного интервала Р=0,997, значения погрешностей можно полагать грубыми, т.е.
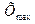 <+3
<+3 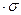 ;
; 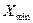 <-3
<-3 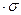 . (4.1)
. (4.1)
Метод размаха. Имеется статистический ряд измерений, для которого вычисляется размах 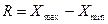 и коэффициент размаха
и коэффициент размаха
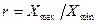 (4.2)
(4.2)
Возможны три варианта. Первый вариант - 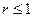 . В этом случае грубые ошибки отсутствуют. Второй вариант -
. В этом случае грубые ошибки отсутствуют. Второй вариант - 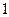 <
< 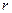 <
< 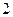 . Возможны грубые ошибки, и это прежде всего крайние значения
. Возможны грубые ошибки, и это прежде всего крайние значения 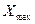 и
и 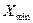 . Исключение грубых ошибок производится следующим образом. Вычисляются предельные значения измерений, которые не считаются грубыми ошибками:
. Исключение грубых ошибок производится следующим образом. Вычисляются предельные значения измерений, которые не считаются грубыми ошибками:
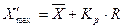 ;
; 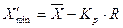 ,(4.3)
,(4.3)
где 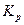 - коэффициент, принимаемый в зависимости от числа членов статистического ряда:
- коэффициент, принимаемый в зависимости от числа членов статистического ряда:
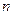 … 4 5 6 7-8 9-10 11-15
… 4 5 6 7-8 9-10 11-15
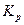 … 1,4 1,3 1,2 1,1 1,0 0,9
… 1,4 1,3 1,2 1,1 1,0 0,9
Значения 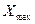 >
>  и
и 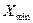 <
< 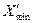 исключаются из ряда как грубые погрешности.
исключаются из ряда как грубые погрешности.
Третий вариант- 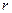 >
> 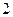 . Наличие грубых ошибок проверяется по коэффициенту вариации
. Наличие грубых ошибок проверяется по коэффициенту вариации 
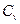 :
:
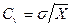 . (4.4)
. (4.4)
Ряд подлежит анализу с целью проверки наличия грубых ошибок, если 

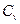 >
> 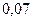 при
при 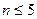 ,
, 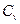 >
> 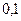 при
при 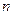 >
> 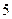 (4.5)
(4.5)
Вычисляются коэффициенты 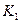 и
и 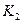 по формулам:
по формулам:
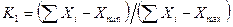 ; (4.6)
; (4.6)
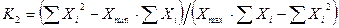 , (4.7)
, (4.7)
где 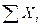 ,
, 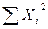 - сумма и сумма квадратов всех измерений ряда. При
- сумма и сумма квадратов всех измерений ряда. При 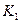 <
< 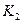 исключаются
исключаются 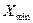 , при
, при 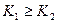 исключаются
исключаются 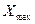 .
.
Метод 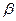 -критерия. Имеется ряд из
-критерия. Имеется ряд из 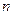 членов, подчиняющийся закону нормального распределения. При анализе ряда с целью установления грубых ошибок вычисляются коэффициенты
членов, подчиняющийся закону нормального распределения. При анализе ряда с целью установления грубых ошибок вычисляются коэффициенты
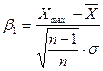 ;
; 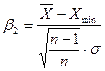 . (4.8)
. (4.8)
Если 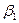 >
> 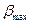 , то значение
, то значение 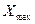 следует исключить из ряда как грубую погрешность, если
следует исключить из ряда как грубую погрешность, если  <
< 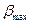 , то исключается
, то исключается 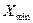 . Величина
. Величина 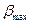 принимается по табл. 4.1 в зависимости от
принимается по табл. 4.1 в зависимости от 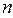 и
и  .
.
Таблица 4.1. Значения 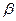 -критерия
-критерия
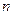
| Величина при 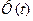
| 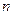
| Величина при 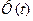
| ||||
| 0,90 | 0,95 | 0,99 | 0,90 | 0,95 | 0,99 | ||
| 1,41 1,64 1,79 1,89 1,97 2,04 2,10 2,15 2,19 2,23 2,26 2,30 | 1,41 1,69 1,87 2,00 2,09 2,17 2,24 2,29 2,34 2,39 2,43 2,46 | 1,41 1,72 1,96 2,13 2,26 2,37 2,46 2,54 2,61 2,66 2,71 2,76 | 2,33 2,35 2,38 2,40 2,43 2,45 2,54 2,61 2,67 2,72 2,76 2,80 | 2,49 2,52 2,55 2,58 2,60 2,62 2,72 2,79 2,85 2,90 2,95 2,99 | 2,80 2,84 2,87 2,90 2,93 2,96 3,07 3,16 3,22 3,28 3,33 3,37 |
Довольно простым и достаточно точным является способ нормирования сомнительных вариант по отношению к их средней арифметической. Нулевой гипотезой при этом служит предположение, что «выскакивающие» варианты принадлежат к той же генеральной совокупности, что и все другие варианты выборки. Критерием оценки нулевой гипотезы служит нормированное отклонение
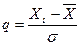 (4.9)
(4.9)
Варианта выбраковываемся, если она выходит за пределы доверительного интервала, устанавливаемого для известного порога вероятности (по прави-лу «плюс-минус трех сигм»).
Описанный способ дает безошибочные результаты лишъ применительно к выборкам большого объема, распределяющегося по нормальному закону. Относительно же малочисленных выборок (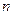 < 30) он не гарантирует надежность оценок. Дело в том, что в малочисленных совокупностях сильнее сказывается зависимость, существующая между величиной нормированного отклонения и числом наблюдений. Поэтому на малочисленных выборках нормировать "выскакивающие" варианты следует с поправкой, равной
< 30) он не гарантирует надежность оценок. Дело в том, что в малочисленных совокупностях сильнее сказывается зависимость, существующая между величиной нормированного отклонения и числом наблюдений. Поэтому на малочисленных выборках нормировать "выскакивающие" варианты следует с поправкой, равной 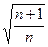 , на которую умножается среднее квадратическое отклонение эмпирической совокупности, т.е. критерием оценки должно служить отношение
, на которую умножается среднее квадратическое отклонение эмпирической совокупности, т.е. критерием оценки должно служить отношение
 (4.10)
(4.10)
Для оценки «выскакивающих» вариант построена специальная таблица, в которой содержатся критические значения нормированного отклонения для разных уровней доверительной вероятности  и числа наблюдений (
и числа наблюдений (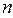 ) (табл. 4.2).
) (табл. 4.2).
После анализа статистического ряда (исключения грубых ошибок) вычис-ляют показатель стабильности по формуле
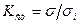 , (4.11)
, (4.11)
где 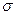 - среднеквадратичное значение контролируемого показателя для стабильного процесса;
- среднеквадратичное значение контролируемого показателя для стабильного процесса; 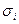 - среднеквадратичное значение
- среднеквадратичное значение 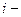 й выборки.
й выборки.
При 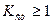 процесс стабилен. Если
процесс стабилен. Если 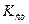 <
< 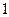 , то необходимо регулирование технологического процесса.
, то необходимо регулирование технологического процесса.
Таблица 4.2. Стандартные значения критерия 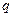 для браковки грубых ошибок
для браковки грубых ошибок
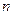
| Значение 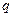 при при 
|
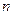
| Значение 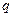 при при 
| ||||||
| 0,95 | 0,98 | 0,99 | 0,999 | 0,95 | 0,98 | 0,99 | 0,999 | ||
| 15,56 4,97 3,56 3,04 2,78 2,62 2,51 2,43 2,37 2,33 2,29 2,26 2,24 2,22 2,20 | 39,00 8,04 5,08 4,10 3,64 3,36 3,18 3,05 2,96 2,89 2,83 2,78 2,74 2,71 2,68 | 78,00 11,46 6,53 5,04 4,36 3,96 3,71 3,54 3,41 3,31 3,23 3,17 3,12 3,08 3,04 | 9,43 7,41 6,37 5,73 5,31 5,01 4,79 4,62 4,48 4,37 4,28 4,20 | ∞ | 2,18 2,17 2,145 2,105 2,079 2,061 2,048 2,038 2,030 2,018 2,009 2,003 1,998 1,994 1,960 | 2,66 2,64 2,60 2,33 | 3,01 2,98 2,932 2,852 2,802 2,768 2,742 2,722 2,707 2,683 2,667 2,655 2,646 2,639 2,576 | 4,13 4,07 3,979 3,819 3,719 3,652 3,062 3,565 3,532 3,492 3,462 3,439 3,423 3,409 3,291 |
Примечание: для нахождения критических значений 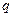 , не указанных в таблице, используется следующая интерполяционная формула:
, не указанных в таблице, используется следующая интерполяционная формула:
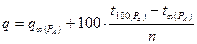 (4.12)
(4.12)
Мерой рассеяния характеристик является среднеквадратичное отклонение 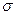 и математическое ожидание
и математическое ожидание 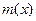 . Математическое ожидание случайной величины определяет среднее значение для теоретического распределения генеральной совокупности:
. Математическое ожидание случайной величины определяет среднее значение для теоретического распределения генеральной совокупности:
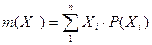 , (4.13)
, (4.13)
где 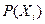 -вероятности случайных значений.
-вероятности случайных значений.
Для теоретической кривой распределения
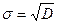 , (4.14)
, (4.14)
где 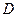 - дисперсия генеральной совокупности
- дисперсия генеральной совокупности
 (4.15)
(4.15)
Для определения 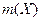 необходимы или большая выборка
необходимы или большая выборка 
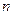 >
> 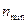 (более 30 измерений), или выполнение сплошных измерений, что является трудоемким и неэкономичным. На практике же обычно используется малая выборка. В этом случае существует такая постановка задачи: значима ли ошибка
(более 30 измерений), или выполнение сплошных измерений, что является трудоемким и неэкономичным. На практике же обычно используется малая выборка. В этом случае существует такая постановка задачи: значима ли ошибка 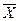 -
- 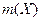 при заданной доверительной вероятности
при заданной доверительной вероятности  . Если эта ошибка не значима, то при контроле качества соблюдаются требования точности и вместо
. Если эта ошибка не значима, то при контроле качества соблюдаются требования точности и вместо 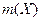 можно контролировать величину
можно контролировать величину 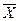 .
.
Если квадратичное отклонение генеральной совокупности 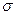 неизвестно, то за критерий стабильности технологического процесса принимают нормированное отклонение
неизвестно, то за критерий стабильности технологического процесса принимают нормированное отклонение 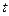 для двух выборок.
для двух выборок.
Решение задачи сводится к расчету критерия 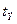 по экспериментальным замерам. Критерий /
по экспериментальным замерам. Критерий / 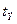 / вычисляется по формуле
/ вычисляется по формуле
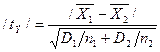 (4.16)
(4.16)
Если 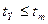 , то разность
, то разность 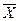 -
- 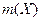 не значима и разрешается вместо
не значима и разрешается вместо 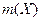 принимать среднеарифметическое
принимать среднеарифметическое 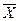 с уровнем значимости
с уровнем значимости 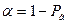 . В этом случае стабильность качества по времени соблюдается.
. В этом случае стабильность качества по времени соблюдается.
Решение рассматриваемой задачи основывается на законе нормального распределения с математическим ожиданием 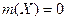 и дисперсией
и дисперсией 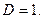
Значение 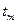 определяется в зависимости от уровня значимости
определяется в зависимости от уровня значимости 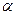 :
:
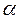 … 0,1 0,05 0,01 0,005 0,0027
… 0,1 0,05 0,01 0,005 0,0027
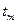 … 1,645 1,96 2,576 2,808 3,00
… 1,645 1,96 2,576 2,808 3,00
4.2. Методика выполнения
В основе работы лежит анализ двух выборок, взятых через определенное время Т. В качестве выборок преподаватель может предложить сравнить во времени стабильность технологических процессов, размеров конструкций, показаний приборов с целью контроля их отклонений от нормативных значений.
Производят статистический анализ результатов замеров и исключают грубые ошибки, которые возникают из-за различных случайных ошибок, с помощью зависимостей (см. 4.1- 4.10).
После выбраковки «выскакивающих» вариант вычисляют показатель стабильности 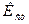 по формуле (4.11). Среднее квадратическое отклонение
по формуле (4.11). Среднее квадратическое отклонение 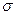 генеральной совокупности приникают по размаху
генеральной совокупности приникают по размаху 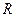 . С этой целью используют выражение
. С этой целью используют выражение
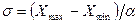 , (4.17)
, (4.17)
где 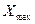 и
и 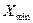 - соответственно максимальное и минимальное значения ранжированного ряда двух выборок после отбрасывания выскакивающих значений;
- соответственно максимальное и минимальное значения ранжированного ряда двух выборок после отбрасывания выскакивающих значений; 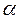 - находят по табл. 4.3 в зависимости от числа измерений
- находят по табл. 4.3 в зависимости от числа измерений 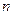 .
.
Таблица 4.3. Значения параметра 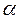 в зависимости от числа измерений
в зависимости от числа измерений 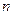
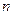
| 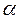
| 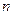
| 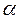
| 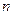
| 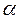
|
| 1,128 1,693 2,059 2,326 2,534 2,704 2,847 | 2,970 3,078 3,173 3,258 3,336 3,407 3,472 | 3,532 3,588 3,640 3,689 3,735 3,850 4,000 |
Затем вычисляют среднеквадратические отклонения, для каждой выборки 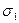 и
и 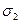 с учетом исключения грубых ошибок. Оценивают стабильность процесса по значениям коэффициентов стабильности
с учетом исключения грубых ошибок. Оценивают стабильность процесса по значениям коэффициентов стабильности 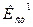 и
и 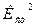 .
.
Решают исходную задачу для случая, когда квадратичное отклонение генеральной совокупности 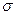 неизвестно. Используя характеристики распределений улучшенных рядов двух выборок
неизвестно. Используя характеристики распределений улучшенных рядов двух выборок 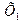 и
и  ,
, 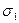 и
и 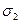 , вычисляют критерий
, вычисляют критерий 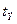 по экспериментальным данным. Сравнивают нормированное отклонение
по экспериментальным данным. Сравнивают нормированное отклонение 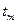 с экспериментальным для всех уровней значимости
с экспериментальным для всех уровней значимости 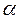
Делают общие выводы о стабильности технологического процесса по различным методикам.
4.3. Схема оформления
Лабораторная работа №
Статистическое регулирование стабильности технологического процесса
1. Анализируемый процесс___________________________________
______________________________________________________________
2. Допуск на данный процесс_________________________________
3. Результаты измерений по выборкам
| Выборка №1 | Выборка №2 | ||
| Номер замера | Фактическое значение параметра 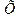
| Номер замера | Фактическое значение параметра 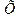
|
…
| 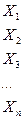
|
…
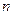
| 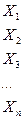
|
4. Исключение грубых ошибок
4.1. «Выскакивающие» варианты по методу трех сигм______________
4.2. «Выскакивающие» варианты по методу размаха_______________
4.3. «Выскакивающие» варианты по методу критерия______________
4.4. «Выскакивающие» варианты по отношению их средней
арифметической______________________________________________
5. Ранжирование рядов результатов измерений по выборкам после отбрасывания выскакивающих вариант
Выборка№1
1 2 3 4 5 … 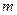
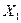
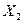
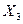
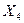
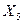 …
… 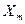
Выборка№2
1 2 3 4 5 … 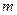
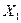
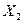
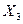
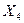
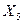 …
… 
6. Статистическая обработка ранжированных рядов во выборкам по п.3 «Схемы оформления» работы № 3 с вычислением среднеарифметических значений 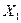 и
и 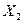 и среднеквадратических отклонений
и среднеквадратических отклонений 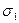 и
и 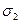 .
.
7. Нахождение по табл. 4.3 параметра 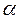 в зависимости от числа изме-рений генеральной совокупности
в зависимости от числа изме-рений генеральной совокупности 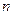 .
.
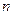 =_________;
=_________; 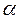 =_________.
=_________.
8. Вычисление среднего квадратического отклонения 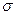 генеральной совокупности по формуле 4.17.
генеральной совокупности по формуле 4.17. 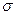 =__________.
=__________.
9. Определение коэффициента стабильности 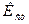 по формуле 4.11
по формуле 4.11
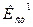 =__________;
=__________; 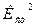 =__________
=__________
10. Выводы о стабильности технологического процесса____________
_______________________________________________________
11. Вычисление критерия 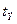 по формуле 4.16.
по формуле 4.16. 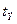 =_______
=_______
12. Выводы о стабильности технологического процесса по нормиро-ванному отклонению 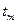 для двух выборок в зависимости от уровня значимости
для двух выборок в зависимости от уровня значимости 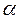 .
.
13. Общие выводы о стабильности технологического процесса по различ-ным методикам.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 490; Нарушение авторских прав?; Мы поможем в написании вашей работы!