Основные теоретические положения. Моделирование оптических приборов и определение их увеличения

Моделирование оптических приборов и определение их увеличения

Цель работы: изучение основных законов геометрической оптики, моделирование микроскопа и зрительных труб Кеплера и Галилея, определение их увеличения.

Основные определения, законы геометрической оптики и свойства линзовой системы смотри в описании лаб. раб. № 1.

Зрительная труба и микроскоп представляют собой оптические приборы, состоящие из двух оптических систем. Оптическая система обращённая к объекту наблюдения называется объективом, а обращённая к глазу наблюдателя – окуляром. Каждую из оптических систем для простоты можно представить тонкими линзами. Собирающая линза L ₁ (объектив) создаёт действительное перевёрнутое изображение предмета, которое рассматривается глазом через линзу L ₂ – окуляр.

Зрительная труба предназначена для рассматривания глазом удалённых предметов. Так как предмет удалён на значительное расстояние, то его уменьшенное изображение находится практически в задней фокальной плоскости объектива. Задний фокус объектива почти совпадает с передним фокусом окуляра, поэтому из окуляра выходят пучки параллельных лучей, что удобно для наблюдения нормальным глазом в спокойном состоянии, т. е. без аккомодации (аккомодация – процесс изменения кривизны хрусталика глаза, с помощью которого достигается приведение изображения предметов, лежащих на различных расстояниях, точно на поверхность чувствительного слоя сетчатки).

Окуляр зрительной трубы может быть как собирающей, так и рассеивающей системой. Зрительная труба с собирающим окуляром называется трубой Кеплера, а труба с рассеивающим окуляром – трубой Галилея. На рис. 2.1 представлен ход лучей при отсутствии трубы (а) в трубе Кеплера (б) и трубе Галилея (в). На рис. 2.1(а) лучи исходящие от удалённого предмета, имеющего линейный размер 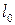, падают под некоторым углом 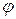к главной оси в глаз человека, при этом на сетчатке глаза формируется изображение линейного размера l.

На рис. 2.1(б) те же лучи падают на объектив L ₁, который собирает их в точке 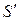, то есть даёт действительное перевёрнутое изображение размером 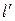в своей фокальной плоскости. Расходящийся пучок лучей из точки 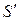падает на окуляр L ₂, так как точка 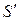лежит в фокальной плоскости окуляра, то из него выходит пучок, параллельный побочной оптической оси 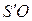под углом 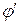к главной оси. Попадая в глаз, лучи эти сходятся в точке 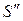на его сетчатке и дают изображение предмета размером 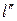. На рис. 2.1(в) глаз не изображён, чтобы не загромождать рисунок. Так как глаз является собирающей оптической системой, которая так же переворачивает изображение, с помощью трубы Галилея человек видит прямое изображение предмета, а с помощью трубы Кеплера – перевёрнутое.

а)  

б)  

в)  

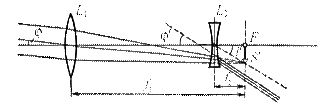
Рис.2.1 Ход лучей в отсутствие оптической системы (а), через трубу Кеплера (б) и Галилея (в).

Найдём формулу расчёта увеличения зрительной трубы. Для характеристики увеличения, даваемого оптической системой, используется величина, называемая углом зрения. Углом зрения называется угол, под которым глаз видит предмет и изображение предмета. На рис.2.1 углы 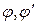– углы зрения.

Длину 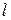изображения на сетчатке глаза в отсутствие зрительной трубы можно найти из выражения

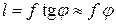, (2.1)

где 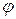малый угол, f – фокусное расстояние глаза наблюдателя как оптической системы.

Вооружённый трубой глаз формирует изображение длиной 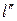, которая определяется аналогичным выражением

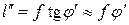. (2.2)

Тогда угловое увеличение 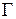равно

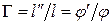. (2.3)

С помощью рис. 2.1 находим

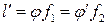, (2.4)

следовательно,

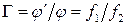, (2.5)

т.е. угловое увеличение зрительной трубы равно отношению фокусных расстояний объектива и окуляра.

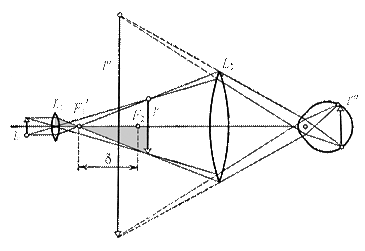
Микроскоп используется для получения больших увеличений, т. е. дает возможность рассматривать изображение предмета под большим углом, чем это возможно для невооруженного глаза. Ход лучей в микроскопе показан на рис.2.2, где объектив и окуляр заменены на рисунке простыми линзами.

Рис.2.2 Ход лучей в микроскопе.

Небольшой предмет, имеющий линейный размер l ₀, помещается перед объективом L ₁ микроскопа на расстоянии, немного большем фокусного расстояния объектива, его действительное изображение длиной 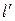находится вблизи переднего фокуса F ₂ окуляра L ₂ – между окуляром и его передним фокусом. Это изображение рассматривается глазом через окуляр, как через лупу, на сетчатке глаза образуется изображение 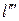, которое воспринимается глазом как исходящее от мнимого увеличенного изображения 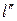. 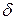– расстояние между задним фокусом объектива и передним фокусом окуляра – называется оптической длиной тубуса микроскопа; как будет показано ниже от нее зависит увеличение микроскопа. Изображение 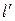находится вблизи передней фокальной плоскости окуляра. Подстройка микроскопа наблюдателем проводится таким образом, чтобы изображение 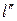находилось на расстоянии ясного зрения .

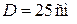Угловое увеличение микроскопа находим как отношение длины изображения 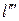к длине l изображения, возникающего на сетчатке невооружённого оптическими приборами глаза

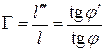, (2.6)

где 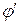– угол зрения, под которым наблюдается изображение 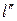, т. е 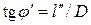. 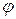– угол зрения, под которым наблюдается предмет 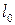невооружённым глазом на том же расстоянии L, на котором наблюдался предмет с помощью микроскопа, т. е. .

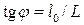Следовательно, формула для увеличения принимает вид:

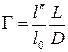. (2.7)

С учётом того, что изображение 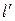лежит вблизи фокуса 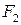окуляра, из выделенных на рис. 2.3 треугольников можно видеть

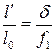, (2.8)

где 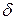– расстояние между фокусами линз 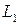и 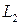. Так же по формуле увеличения тонкой линзы длины изображени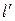й и 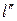можно связать формулой

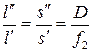, (2.9)

где 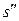– расстояние от мнимого изображения 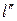до линзы, если пренебречь расстоянием от глаза до линзы, то 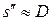; 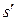– расстояние от линзы до изображения 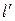, так как оно лежит вблизи фокуса 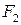, то .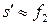

Выражая из (2.8) 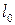, а из (2.9) 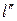и подставляя в (2.7), получаем формулу для расчёта увеличения микроскопа

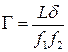. (2.10)

Дата добавления: 2015-06-04