Обработка результатов измерений. Этап 1 – предварительная подготовка к проведению эксперимента

ОСНОВНЫЕ ЭТАПЫ ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

Этап 1 – предварительная подготовка к проведению эксперимента.

Предварительная подготовка заключается в изучении теории явления, которое исследуется в лабораторной работе, в изучении метода и схемы измерений, принципа действия, конструкции и условий эксплуатации физических приборов, используемых в работе, в составлении плана предстоящих измерений по каждому заданию работы.

Результатом предварительной подготовки является письменный конспект, вносимый в рабочую тетрадь в виде короткого, но ясного изложения. Конспект к лабораторной работе составляется при самостоятельной подготовке студента к лабораторной работе и предъявляется преподавателю на аудиторном лабораторном занятии. Без предварительной подготовки к лабораторной работе и конспекта студент не допускается к выполнению эксперимента.

Этап 2 – проведение эксперимента.

До начала выполнения эксперимента необходимо визуально ознакомиться с устройством стенда, оценить цену деления шкалы всех приборов, используемых для измерений, взять все принадлежности, необходимые для работы, а также узнать у преподавателя постоянные параметры, при которых проводятся экспериментальные измерения. Результаты измерений надо сразу же вносить в таблицу измерений.

После проведения эксперимента необходимо на рабочем месте, не разбирая измерительной установки, оценить окончательный результат для одного опыта по измеренным величинам. В случае неудовлетворительного результата измерения необходимо провести вновь.

Этап 3 – сдача зачета по выполненной лабораторной работе.

Зачет по выполненной лабораторной работе включает в себя защиту теории по контрольным вопросам и представление письменного отчета, в котором помимо данных предварительной самостоятельной подготовки (конспекта) приведены как первичные результаты эксперимента, так и окончательная обработка результатов (расчет искомых величин, оценка погрешностей их измерения, графики, выводы с анализом полученных результатов).

К сдаче итогового зачета (экзамена) по физике допускаются только студен-

ты, выполнившие полный объем лабораторных работ за семестр.

В физике основным способом получения информации является измерение. Измерение - нахождение значения физической величины опытным путем с помощью специальных технических средств.

Как бы ни были совершенны приборы и постоянны условия, при которых производятся измерения, всегда определяются только приближенные значения измеряемой величины, а возникающая при этом погрешность характеризует точность измерений. Погрешности возникают из-за конструктивных недостатков приборов, из-за трения между подвижными частями, усталости упругих элементов, изменения параметров среды в процессе эксперимента, ошибок экспериментатора при градуировке приборов, наводке, считывании результатов и т.д.

Погрешности разделяются на три вида: случайные, систематические и промахи.

Случайными называются погрешности, которые при многократных повторениях опыта изменяются нерегулярным, непредсказуемым образом, приводя к разбросу измеренных значений; их нельзя устранить при обработке результатов измерений.

Систематическими называются погрешности измерений, происходящие в результате действия постоянных причин, при повторных измерениях в одинаковых условиях тем же методом они остаются постоянными по величине и по знаку, либо изменяются закономерно, в зависимости от тех или иных факторов. Влияние систематических погрешностей может быть выявлено и учтено при обработке эксперимента введением поправки либо предельной систематической погрешности.

Промахи (грубые ошибки) представляют собой случайные погрешности, величина которых резко превышает допустимые и искажает результаты измерения. Они возникают вследствие неисправности прибора, невнимательности наблюдателя, при резком нарушении методики эксперимента или условий его проведения. Промахи выявляются при повторных измерениях и исключаются из результатов измерений.

Под абсолютной погрешностью Dх измерения понимают разность между изме-ренным х_изм и истинным х_ист значениями физической величины:

Dх = х_изм – х_ист. (1)

При выполнении лабораторных работ допускается упрощенная методика обработки экспериментальных данных. Суть ее состоит в следующем.

1. Так как истинное значение х_ист измеряемой физической величины часто неизвестно, как и конкретные причины погрешностей, то все ошибки, которые меняются от опыта к опыту и вызывают разброс результатов, рассматривают как случайные и называют ошибками разброса. При отсутствии информации о причинах наблюдаемого разброса за наиболее вероятное значение измеряемой величины принимается среднее арифметическое из измеренных значений:

, (2)

где х₁, х₂, …, х_n - измеренные значения физической величины; n - число измерений.

При большом числе измерений среднее арифметическое <х> из измеренных значений можно считать равным истинному значению физической величины х_ист:

<х> = х_ист.

2. Отклонением D x_i результатов отдельных измерений x_i от среднего <х> называется величина

D x_i = x_i - < x >, (3)

которую можно принять за абсолютную погрешность отдельных измерений, где

i =1, 2, …, n.

3. Если ширина разброса отражает все погрешности (как случайные, так и систематические), то за меру точности в упрощенной методике обработки результатов измерений принимают среднююабсолютную погрешность по разбросу

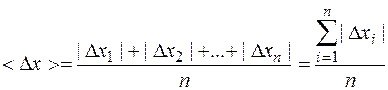, (4)

являющуюся средним арифметическим из абсолютных значений отклонений |D x_i | результатов отдельных измерений х_i от среднего <х>.

4. Измеренная физическая величина х_изм всегда записывается вместе с погрешностью:

х_изм = <х> ± <Dх>, (5)

что эквивалентно неравенству . Интервал <х> ± <Dх> называется доверительным интервалом, отвечающим доверительной вероятности b. Доверительная вероятность интервала <х> ± <Dх> равна 75-80 % при условии, что число измерений не меньше 4-5, и выше, если сделано более пяти измерений.

5. С редней относительной погрешностью измерения называется величина

. (6)

Относительная погрешность выражается в процентах. Точность определения средней относительной погрешности при упрощенной обработке результатов невелика, поэтому следует ограничиваться целыми числами, если d_x ³ 2 %, и округлить d_x до 1,0 или 1,5 %, если d_x £ 1,5 %.

Правила округления физических величин при вычислениях

При математических действиях с физическими величинами, измеренными с определенными погрешностями, необходимо следить, чтобы сам процесс вычислений не вносил дополнительной ошибки. Поэтому:

1) произведение (или частное) не может быть записано с бо¢льшим числом цифр,

чем наименее точно известный сомножитель;

2) при сложении и вычитании надо сохранять цифру десятичного разряда, следующего за тем, который сохранен в наименее точно известном слагаемом;

3) величины, значения которых берутся из таблиц (математические и физические константы) также следует брать с числом цифр, на единицу бо¢льшим, чем в самом неточном из измеренных чисел.

При выполнении указанных правил в ответе число верных знаков будет на один меньше, чем у исходного числа с наименьшим числом верных знаков.

Числа следует округлять по следующему правилу:

1) если последняя цифра меньше 5, то остающиеся цифры не изменяются; например, вместо 12,731 после округления получим 12,73;

2) если последняя цифра больше 5, то предпоследнюю цифру увеличивают на единицу: т.е. вместо 12,736 имеем 12,74;

3) если последняя цифра равна 5, то при наличии предыдущей нечетной цифры последнюю увеличивают на единицу, а при наличии четной – цифру 5 отбрасывают; например, для 12,735 округленное число равно 12,74, а для 12,745 оно остается равным 12,74.

Дата добавления: 2015-06-04