Из выражения (5.15) и (5.16) получаем

По закону Фарадея ЭДС индукции по вторичной обмотке

(5.12)

где Ф – поток вектора магнитной индукции через один виток; S₂ – площадь поперечного сечения тороида.

По закону Кирхгофа для вторичной обмотки получаем:

(5.13)

где U_C – напряжение на конденсаторе; I₂ – ток во вторичной обмотке; L₂ – индуктивность вторичной обмотки.

Так как L₂ очень мало, а I₂R₂>>U_C, уравнение (5.13) может быть записано с учетом (5.12) в следующем виде:

.

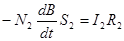Откуда

(5.14)

Учитывая (5.14), найдем напряжение U_у, равное напряжению на конденсаторе

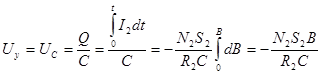(5.15)

где Q – заряд на обкладках конденсатора.

Если известен коэффициент отклонения луча k_у по вертикали, то

U_y=k_yy (5.16)

(5.17)

Подав одновременно напряжения U_у и U_х на вертикально и горизонтально отклоняющиеся пластины, получим на экране осциллографа петлю гистерезиса.

По площади петли можно найти работу перемагничивания, отнесенную к единице объема. Малое изменение объемной плотности энергии магнитного поля в цикле перемагничивания определяется по формуле

(5.18)

Работа расходуется на изменение внутренней энергии единицы объема ферромагнетика. За полный цикл перемагничивания

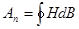(5.19)

Учитывая (5.11) и (5.17), получаем

(5.20)

где S_п – площадь петли гистерезиса; S₂=(r₁-r₂)b.

k_X – коэффициент отклонения по каналу Х; k_X=0,3 В/дел.

Дата добавления: 2015-06-04