Поле объемных зарядов

Напряженность поля, создаваемого объемными зарядами, обладает интересной особенностью: она возрастает при удалении от “центра тяжести” облака объемного заряда. Рассмотрим такое заряженное “облако”, имеющее форму шара (рис. 1). Общий заряд его обозначим д, объемная плотность заряда р предполагается постоянной.

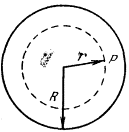рис. 1

Найдем поле в точке Р внутри шара. Разобьем весь объемный заряд на две части: сферу радиуса г и остальную часть шара. Внешняя часть не создает никакого поля в точке Р. Это ясно из того, что ее можно представить себе состоящей из вложенных друг в друга концентрических заряженных сфер, а каждая из них, как мы доказали в предыдущем параграфе, не создает никакого поля в своей внутренней области. Поэтому остается только поле сферы радиуса r, которое равно Е=q/r^{2, где q - ее заряд, равный произведению плотности заряда р на объем: q=4/3pPir3. Следовательно, поле в точке Р равно Е=pr/3E0. Напряженность растет линейно с удалением от центра сферы. Как видно из вывода, этот рост объясняется тем, что при удалении от центра действующий заряд растет как г3, в то время как его поле убывает как 1/r2. Как только мы переходим в область r>R, т. е. выходим за пределы шара, заряд, создающий поле, перестает возрастать и поле убывает обратно пропорционально r2.}

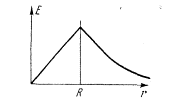^{рис. 2}

^{Рассмотрим теперь, как меняется с расстоянием напряженность поля, создаваемого бесконечным плоским объемно заряженным слоем.}

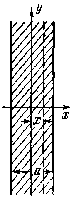^{рис. 3}

^{Его можно мысленно разбить на ряд тонких параллельных плоскостей. Поле плоскости равно 2л и не зависит от расстояния до нее, поэтому поля отдельных плоскостей будут просто складываться. Это значит, что будут складываться заряды, приходящиеся на единицу площади. Общий заряд, приходящийся на единицу площади слева от пунктирной плоскости, будет равен (a/2+x) • 1 • p, а справа (a/2 - x) • 1 • p. Значит, поле, создаваемое зарядом, находящимся слева от пунктирной плоскости, равно 2p Pi(a/2+x), а поле заряда, находящегося справа, 2Pip(a/2-x). Направлены эти поля в противоположные стороны, поэтому результирующее поле будет равно их разности 4pPix. Итак, внутри слоя}

^E=px/E0

^{На границе слоя х = а/2 и Е=2pPiа. Это последнее значение}

^{совпадает с 2л@, (@-сигма)так как на единицу площади слоя приходится заряд, равный a • 1 • p.Получается зависимость Е от x, представленная на рисунке 4. 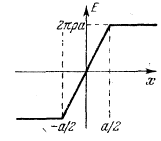рис. 4}

Дата добавления: 2015-06-04