Потенциальные диаграммы

Поле, создаваемое заряженным телом или несколькими телами, наглядно может быть представлено с помощью так называемой потенциальной диаграммы-

графика зависимости потенциала или потенциальной энергии от координат.

Рассмотрим несколько типичных потенциальных диаграмм. В качестве первого примера построим зависимость потенциала положительного точечного заряда ф == q/r от расстояния r до этого заряда. График этой функции представлен на рис. 8, а (ось абсцисс проведена через заряд). Потенциал неограниченно возрастает (т. е. стремится к бесконечности) при приближении к заряду и медленно уменьшается при удалении от него. Для отрицательного заряда график такой же, только расположен в области ф < 0 (рис. 8, б). Точно такой же вид имеет график потенциальной энергии взаимодействия положительного заряда +q1 и отрицательного -q2 (например электрона и ядра). Если заряд размещен на поверхности сферы, то вне сферы потенциал ф=q/r, т. е. совпадает с потенциалом точечного заряда, помешенного в центре сферы. Внутри сферы Е = 0, поэтому там потенциал постоянен. В результате имеем график, изо-браженный на рис. 8.

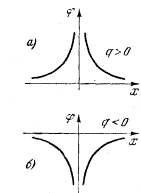рис. 8

Потенциал в плоском конденсаторе. Построим теперь график хода потенциала внутри и вне плоского конденсатора конечных размеров. Внутри конденсатора напряженность поля постоянна. В формуле Е =

= -дельта ф/дельта l можно взять в качестве дельта l расстояние между началом координат и некоторой точкой, имеющей координату х (рис. 9, а). Тогда дельта ф = ф-ф0, где (ф-потенциал в точке с координатой х, а ф0 - в точке х = 0. От-

сюда получаем Е ==- ф-ф0/х, или ф=ф0-Ех. (28.1)

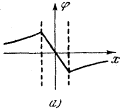рис. 9(а)

Следовательно, график ф(х) -линейная функция х, принимающая наибольшее значение на положительной пластине и наименьшее на отрицательной. Вне конденсатора, при удалении на бесконечность, потенциал должен стремиться к нулю. Наконец, в начале координат, т. е. в центре конденсатора, потенциал ф0 должен равняться нулю, иначе потенциалы пластин не будут равны по величине и противоположны по знаку. В результате получаем график рис. 9, а. Чем больше размеры пластин, тем медленнее спадает потенциал вне конденсатора.

Если потенциал зависит от одной координаты (как, например, в плоском конденсаторе, где он зависит только от одной координаты х), напряженность равна минус производной от потенциала по этой координате:

E=- dф/dx. ^{Графически на потенциальных диаграммах}

^{напряженность есть тангенс угла наклона касательной к кривой ф(х) с осью Ох. Следовательно, напряженность и сила, действующая на заряд, больше там, где график идет круче, т. е. составляет больший (более близкий к 90°) угол с осью Ох. Там, где график ф(x) параллелен оси Ох, напряженность равна нулю. Рассмотрите с этой точки зрения все потенциальные диаграммы этого параграфа,}

^{Скачок потенциала на двойном слое. Чем ближе пластины друг к другу, тем круче ход потенциала между}

^{ними. Две близкие поверхности, имеющие равные и противоположные по знаку заряды, составляют так называемый двойной слой. Потенциал на двойном слое совершает скачок (см. рис. 74,6), подобно тому как на заряженной поверхности имеется скачок на-пряженности.}

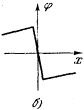^{рис. 9(б)}

^{Потенциал системы из двух заряженных сфер . Рассмотрим ход потенциала, создаваемого системой из двух}

^{концентрических сфер. Пусть внутренняя сфера радиуса R1 имеет положительный заряд q1, а внешняя радиуса R2-отрицательный заряд q2 (см. рис. 10, на котором положено q1>\q2\).}

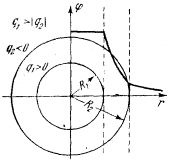^{рис. 10}

^{Тогда вне сфер потенциал будет равен ф=(q1+q2)/r (СГС), (28.2) так как его создают совместно обе сферы. Напомним, что потенциал есть работа внешних сил, совершаемая при перемещении +1 заряда в данную точку из бесконечности. Работа перенесения +1 заряда из бесконечности в область между сферами будет равна сумме двух работ: q2/R2 (работе против сил, действующих со стороны внешней сферы на пути из +бесконечности до ее поверхности) и q1/r (работе против поля внутренней сферы):}

^{ф=q2/R2 + q1/r (СГС). (28.3)}

^{Наконец, внутри меньшей из сфер потенциал будет постоянен и равен Ф = ф=q2/R2 + q1/R1 (это значение получается}

^{из формулы (28.3) при подстановке в нее г ==R1)). По формулам (28.2), (28.3) легко построить график рис. 10.}

^{Сферический конденсатор имеет заряды обкладок, равные по величине и противоположные но знаку: q2= =-q1, так что потенциал (28,2) во внешней области обращается в нуль, а между обкладками (28.3) равен}

^{ф=q1(1/r-1/R2). (28.4)}

^{Получается график рис. 11. Если внутренняя сфера имеет отрицательный заряд, а внешняя положительный, график переворачивается (рис. 12).}

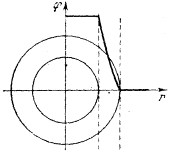^{рис. 11 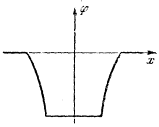рис. 12}

^{Потенциальная яма . Представим себе две концентрические сферы, сделанные из густой металлической сетки. Знак внутренней сферы, положителен, внешней - отрицателен. Потенциальная энергия электрона, U=eф, помещенного внутрь такой системы, выглядит так, как потенциал на рис. 12 (поскольку заряд электрона е отрицателен). Такой ход потенциальной энергии носит название потенциальной ямы. Происхождение названия ясно из рисунка. Пока электрон находится внутри меньшей из сфер, на него не действуют никакие силы. Если он попадает в промежуток между сферами, на него действуют силы возвращающие его во внутреннюю область (внешняя сфера заряжена отрицательно и отталкивает его, внутренняя - положительно). Электрон, двигаясь на-ружу, замедляется, выполняя работу против этих сил.}

^{Потенциальная яма не обязательно имеет плоское “дно”. На рис. 8 тоже изображена потенциальная яма, которую заряд одного знака создает для заряда противоположного знака.}

^{Объемно заряженная сфера, т. е. заряженное “облако”, также является потенциальной ямой для заряда противоположного знака. Ход потенциальной энергииU=qф показан на рис. 13. Помещенный в облакоположительного заряда электрон будет притягиваться к центру облака.}

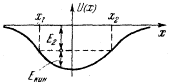^{рис. 13}

^{Кинетическая и потенциальная энергия частицы в потенциальной яме . Полная энергия электрона (сумма кинетической и потен-циальной энергий) при движении в потенциальном поле сохраняется. На рис. 13}

^{пунктиром показан один из возможных уровней энергии электрона Е1. Энергия откладывается от оси х, так что рассматриваемый уровень соответствует положительной полной энергии (E1>0). Поскольку Е1 = Екин + U (a U отрицательна!), нетрудно сообразить, что кинетическая энергия равна отрезку, проведенному от кривой U(x) до уровня E1.}

^{При движении из центра наружу, например вправо, на электрон действуют тормозящие силы, кинетическая энергия уменьшается, потенциальная возрастает. Когда электрон удалится достаточно далеко, потенциальная энергия станет близкой к нулю (см. график), а кинетическая станет равна полной энергии Е1.}

^{Следовательно, частица, обладающая положительной полной энергией, может выйти из потенциальной ямы, и у нее еще останется кинетическая энергия, равная E1.}

^{На рис. 14 в такую же потенциальную яму помещена частица с отрицательной полной энергией E2.}

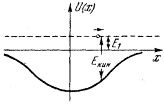^{рис. 14}

^{Удивляться тому, что полная энергия может быть отрицательной, не следует: ведь полная энергия равна сумме кинетической. н потенциальной, а потенциальная энергия в данном случае отрицательна. Отрицательность полной энергии означает просто, что кинетическая энергия частицы мала.}

^{Кинетическая энергия на графике снова равна отрезку, проведенному от кривой U(x) до уровня энергии Е2 (см. рис. 14).}

^{В точках пересечения уровня Е2 с кривой U(x), т. е. в точках с координатами х1 и Х2, кинетическая}

^{энергия равна нулю, т. е. частица останавливается и поворачивает обратно. Движение частицы с отрицательной полной энергией E2. следовательно, колебательное - частица движется от левой “стенки” к правой и наоборот. Выйти из потенциальной ямы такая частица не может.}

^{Потенциальный барьер . В заключение рассмотрим так называемый потенциальный барьер.}

^{Если облако 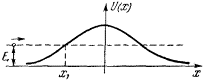рис. 15}

^{объемного заряда за* ряжено отрицательно, то график потенциальной энергии электрона, проходящего через такую область, имеет вид рис. 15. Электрон, подходящий к барьеру, тормозится. Если его}

^{полная энергия Е ниже гребня потенциального барьера, он остановится в точке х1 и повернет обратно. Пройти сквозь барьер он не сможет.}

^{Если барьер очень узок, то электрон, вопреки законам классической механики, сможет, с определенной вероятностью, пройти сквозь барьер (туннельный эффект). Причины такого парадоксального поведения электрона - в волновых свойствах частиц малой массы (микрочастиц).}

Дата добавления: 2015-06-04