Сложение и умножение в O-символике

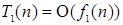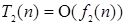Правило суммы. Если и , то 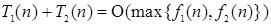. (Аналогичные утверждения справедливы также для множеств и ).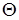

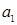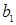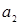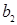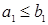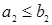Доказательство. (Доказательство этой теоремы основывается простом соотношении для произвольных вещественных чисел , , , : если и , то )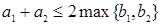

Поскольку , существует константа с ₁ и неотрицательное целое число n ₁ такие, что для всех 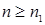справедливо .

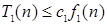По аналогии, поскольку существует константа 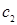и неотрицательное целое число 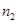такие, что для всех 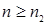справедливо .

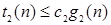Обозначим через 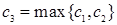и рассмотрим случай, когда верны оба неравенства для случая 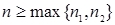. Сложив приведенные выше неравенства, получим

.

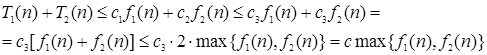Откуда следует, что 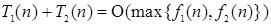. Исходя из определения О-асимптотики, в качестве констант с и 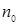положим 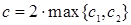и .

При анализе алгоритмов теорема о сумме используется следующим образом. Пусть имеются два фрагмента программы P ₂ и P ₂, причем время выполнения одного , а другого 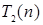. Очевидно, что если эти фрагменты выполняются последовательно, то общее время работы (общая трудоемкость последовательно выполняемых фрагментов) будет равно 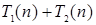. Тогда асимптотическая оценка всего фрагмента по теореме о сумме – 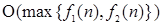. Это означает, что общая эффективность алгоритма зависит от той части, для которой функция роста трудоемкости имеет наибольший порядок роста, т.е. от наименее эффективной его части алгоритма:

.

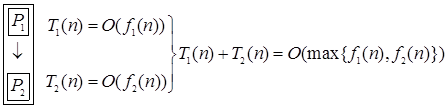Правило произведений. Если T₁(n) и Т₂(п) имеют степени роста O (f ₁(n))и O (f ₂(n))соответственно, то произведение T₁ (n) T₂ (n)имеет степень роста O (f ₁(n) f ₂(n)).

Доказательство аналогично доказательству правило сумм.

Следствие правила произведений. O (cf(n))эквивалентно О (f (п)), где с — положительная константа. Иными словами положительную константу можно вносить и выносить из-под асимптотической функции.

Например, О( 2 п²) эквивалентно О(п²).

Дата добавления: 2015-06-04