Тасымалдау процестері

Диффузия, тұтқырлық және жылуөткізгіштік құбылыстары бір-бірімен ұқсас, себебі газ немесе сұйық арқылы бұндай процестер кезінде кейбір физикалық шамалардың тасымалдауы байқалады. Концентрация градиенті бар болуы себебінен жүйенің бір бөлігінен екіншісіне массаның тасымалдауы диффузия деп аталады; ағын жылдамдықтарының градиенті бар болуы себебінен газ немесе сұйық арқылы жүйенің бір бөлігінен екіншісіне импульстің тасымалдауы тұтқырлық деп аталады; температура градиенті болу нәтижесінде жылулық энергияның жүйенің бір бөлігінен екіншісіне тасымал-дауы жылуөткізгіштік деп аталады. Жалпы осы үш процесті тасы-малдау процестері дейді.Тасымалдау процестерінде заттың, жылулық энергияның және импульстің кеңістік және уақыт бойынша бөлінуі байқалады. Бұл бөлінулер заттың тұтас жүйе (дене) ретінде «таза” механикалық (гидродинамикалық) қозғалысымен де және заттың құрамындағы молекулалардың жылулық қозғалысымен де байланысты болуы мүм-кін. Тасымалдаудың «таза түрі» осы екінші – молекулалардың жылулық қозғалысымен анықталады. Сондықтан, заттың құрамындағы молекулалардың жылулық қозғалысы нәтижесінде кеңістік және уақыт бойынша массаның (заттың) бөлінуі немесе тасымалдануы диффузия деп аталады. Осылай молекулалардың жылулық қозғалысында импульстің тасымалдауы тұтқырлық деп аталады, бұл процесс ортаның (газдың, сұйықтың) деформациялануына әкеледі,нәтижесінде деформациялану жылдамдықтарына тәуелді кернеулер пайда болады.

17. Нақты газдар. Ван-дер-Ваальс теңдеуі. Ван-дер-Ваальс күштері.

Нақты газдың қысымы идеал газдың P қысымынан шамаға кіші болады. қысым газдың ішіне қарай бағытталған, сонд. оны газдың ішкі қысымы д.а. Олай болса Менделеев-Клайперон теңдеуінің орнына қосындысын қоюымыз керек.

қосымша қысымның пайда болуының себепшісі-молекулалардың өзара бір-біріне тартылысы. Сонд. қосымша қысым ~

Молекулалардың сандық тығыздығы V мольдік көлемге кері пропорционал, демек

~

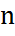Сөйтіп, ~ демек мұндағы пропорционалдық коэф. Сонымен, -нің бойынша анықталған мәнін ға қойсақ, нақты газ күйінің теңдеуін мына түрде жазуға болады:

Осы теңдеу Ван-дер-Вальс теңдеуі деп аталады.

Молекулалар арасындағы тартылыс күштерін ескеру. Моле-кулалар арасындағы тартылыс күштері газдың ыдыстың қабырғала-рына түсірген қысымына ықпалын тигізеді. Ыдыс қабырғасына жақын орналасқан және соған қарай бара жатқан кез келген молекуласына көршілес молекулалар жағынан қорытқы күш әсер етеді. Бұл күш газдың ішіне қарай бағытталады. Осының нәтижесінде молекуласы ыдыстың қабырғасына әлсіреген күшпен соқтығысады. Сол себептен бірдей жағдайларда нақты газдың қысымы идеал газдың p қысымынан шамаға кіші болады. қысым газдың ішіне қарай бағытталған, сондықтан оны газдың ішкі қысымы деп те атауға болады Олай болса (5.16)-дағы идеал газдың қысымы орнына қосындысын қоюы-мыз керек: 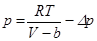немесе . (5.20)

Тартылыс күштері молекулалар-ды жақындатуға тырысады. Сыртқы күштер де тура осылай әсер етеді.

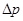қосымша қысымның пайда болуының себепшісі – молекулалар-дың өзара бір-біріне тартылысы. Сондықтан ыдыстың бетіне газ тарапынан түсірілген қысым, осы қабаттың бірлік бетіндегі барлық молекулаларға әсер ететін күшке тең болады.Бұл әрекет етуші күштердің нәти-желік мәні газдың ішіне қарай бағыт-талған. Сол себептен бұл күш моле-кулалардың n сандық тығыздығына пропорционал. Екінші жағынан, осы беттік қабаттағы тартылыс күші әсер ететін молекулалар саны да тығыздыққа пропорционал. Сондықтан қосымша қысым . (5.21)

Молекулалардың сандық тығыздығы мольдік көлемге кері про-порционал, демек .Сөйтіп , демек , (5.22) мұндағы а – пропорциналдық коэффициент, сандық мәні молекула-лардың арасындағы тартылыс күшіне тәуелді.

Сонымен, 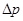-нің (5.22) бойынша анықталған мәнін (5.20)-шы формулаға қойсақ, нақты газ күйінің теңдеуін мына түрде жазуға болады: 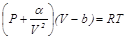. (5.23) Бұл өрнек нақты газдың қысымын, көлемін және температурасын байланыстырады және бір молі үшін анықталған, сондықтан нақты газ күйінің теңдеуі деп аталады. Бұл теңдеуді Ван-дер-Ваальс теңдеуі деп те атайды, ондағы және тұрақты коэффициенттер Ван-дер-Ваальс тұрақтылары делінеді. Ван-дер-Ваальс теңдеуінде тартылыс күштері ( – түзетуші мүше) және тебу күштері ( – түзеткіш) ескерілген. Осы теңдеуде молекула-кинетикалық көзқарастарына сүйеніп, нақты газдың негізгі қасиеттері ескеріліп, алғашқы рет тұжырымдалған.

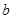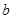тұрақтысының өлшем бірлігі көлеммен сәйкес, яғни м³/моль, ал -ның өлшем бірлігі қысымның бірлігіне сәйкес болады, сондықтан СИ жүйесінде Па·м⁶·м^-2, демек . Әр түрлі газдар үшін және тұрақтыларының мәндері әр түрлі болады.

(5.23)-ші теңдеу бір моль газға қатысты жазылған. Кез келген газдың массасы үшін ол былай жазылады: , (5.24)мұндағы m – газдың массасы, М – мольдік масса, V – газдың көлемі.

18. Бірінші текті фазалық ауысымдар. Күй диаграммалары.

Фазалық ауысу, фазалық түрлену — кең мағынасында сыртқы жағдайлар (температура, қысым, магниттік және электрлік өріс, т.б.) өзгергенде заттың бір фазадан екінші фазаға ауысуы; тар мағынасында сыртқы параметрлер үздіксіз өзгергенде физикалық қасиеттердің секірмелі өзгеруі. Температураның, қысымның немесе қандай да бір басқа физ. шаманың Фазалық ауысу өтетін мәні ауысу нүктесі деп аталады. Фазалық ауысудың екі тегін ажыратады. Бірінші текті Фазалық ауысуда заттың тығыздығы, құраушыларының концентрациясы сияқты термодинамикалық сипаттамалары секірмелі түрде өзгереді; масса бірлігінде Фазалық ауысу жылуы деп аталатын жылудың толық анықталған мөлшері бөлінеді немесе жұтылады. Екінші текті Фазалық ауысу кезінде қандай да бір нөлге тең физикалық шама ауысу нүктесінің бір жағынан екінші жағына қарай ығысу нүктесінен алыстағанда нөлден бастап біртіндеп өседі. Мұнда тығыздық үздіксіз өзгереді, жылу бөлінбейді және жұтылмайды. Бірінші текті Фазалық ауысу табиғатта кең таралған құбылыс. Оған булану мен конденсаттану, балқу мен қатаю, қатты фазаға сублимациялану мен конденсаттану, қатты денелердегі кейбір құрылымдық ауысулар, мысалы, темір-көміртек қорытпасында мартенситтің түзілуі жатады. Таза асқын өткізгіштерде жеткілікті күшті магнит өрісі асқын өткізгіштік күйден қалыпты күйге бірінші текті Фазалық ауысутуғызады. Екінші текті Фазалық ауысуға: макроскоп. магниттік моменттің пайда болуымен бірге жүретінпара-ферромагнетик. ауысу, пара-антиферромагнетик. ауысу, т.б. жатады. Фазалық ауысу температураның, т.б. шамалардың қатаң анықталған мәндеріндегі бөлшектер санына шек қойылмайтын жүйеде ғана өтетін құбылыс.

19. Клапейрон-Клаузиус теңдеуі.

Карно циклының пайдалы әсер коэффицентінің мәні кез-келген денелер үшін бірдей және температураға тәуелді. Карно циклының осы ерекшелігін басқа да термодинамикалық шамалар арасындағы байланысты табуға қолданады. Мысалы сұйықтың қаныққан буының қысымы мен температурасының арасындағы тәуелділікті беретін Клапейрон- Клаузиус теңдеуін шығаруға болады. Температурасы Т сұйық қысымы Р_қ.б өзінің буымен тепе- теңдікте болсын делік. Осы температураға сәйкес сұйықтың молекулалық V_с, будың мелекулалық көлемі V_қ.б болсын (С сұйық, қ.б қаныққан бу).

Р, V диаграмасында (1-сурет) жүйенің бастапқы күйін а нүктесі сипаттайды. Жүйе изотермалық ұлғайып в қалпына барсын делік. Қарастырып отырған жүйе- өз буымен тең-теңдікте болатын сұйық тұрақты қысымда - Р_қ.б изотермиялық кеңейеді, бұл кезде сұйықтың n киломолі буланады. Сұйық күйдегі заттың n киломолінің көлемі n V_с, ал қаныққан бу күйінде оның көлемі

n V_қ.б. Сөйтіп жүйе а күйден 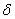-ға көшкенде көлемін n(V_қ.б - V_с, ) шамаға өзгертеді.

1-сурет.

Сұйық изотермиялық түрде булану үшін, жүйеге буланған сұйықтың киломоль санының n булану жылуына көбейтіндісіне тең (n ) жылу беру қажет. Жүйе в нүктесінен көлемін аз ғана шамаға өзгертіп, адиабатты процеспен с нүктесіне өтсін, оның температурасы алғашқыдан dT шамаға төмен. Қаныққан будың қысымы d Р_қ.б –ға кемиді. Жүйені с қалпына d күйіне жеткізу үшін, изотериялық қысамыз да, көлемін азайтамыз, с 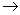d аралыққа өткенде қысым тұрақты болады да, будың белгілі бір мөлшері конденсацияланады. Жүйе d-дан бастапқы а күйіне адиабатты сығылып өтеді де, температурасы бастапқы мәніне жетеді. Осы кездегі Карно циклының толық пайдалы әсер коэффицентін төмендегіше жазуға болады: 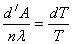(5.1)

d^/ A – бір толық циклда жұмысқа айналған жылу, n - изотермиялық ұлғайғанда жүйеге берілген жылу. 1-суретте d^/ A жұмысы abcd фигурасының ауданына тең. Аудан бір таңбаны мен (ab немесе cd) биіктігінің көбейтіндісінен тұрады, ал ол графиктен қаныққан бу қысымының өзгерісімен d Р_қ.б анықталады. Қарастырып отырған фигураның табаны ab заттың n киломолінің сұйық және бу күйіндегі көлемдерінің айырымына n(V_қ.б - V_с) тең болғандықтан, толық бір циклда заттың істеген жұмысы

d^| A= n(V_қ.б - V_с) d Р_қ.б (5.2)

Толық бір циклдағы пайдалы әсер коэфицентін табу үшін, соңғы өрнекті (5.1) қатынасына қоямыз:

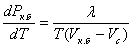бұдан (5.3)

Бұл формула термодинамиканың бірінші бастамасын ашқанға дейін қорытылады және Клапейрон- Клаузиус теңдеуі деп аталады. Бұл теңдеуді пайдалану арқылы термодинамикалық және молекула- кинетикалық тәсілдерді салыстырып, заттың әр күйдегі қысымын, температурасын, меншшікті булану жылуын табуға болады.

Клапейрон- Клаузиус теңдеуін сұйық- бу түріндегі фазалық түзілуге ғана емес басқа да түрлі фазалық түзулерге де қолданылады.

Бұл теңдеу температура өзгергенде әртүрлі фазалар тепе-теңдікте болса да қысымның өзгеретіндігін сипаттайды.

Қаныққан бу қысымының температурадан тәуелділігін табу үшін (5.3) теңдеуді пайдаланайық (бұл температура кризистік температурадан әлдеқайда аз болсын). Онда V_с << V_қ.б және будың бір молі үшін . Осыны Клапейрон-Менделеев теңдеуіне қойып, сұйық көлемін ескерсек

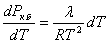(5.4)

-мольдік булану жылуы. температураға тәуелсіз деп алып интегралдасақ немесе Р_қ.б=Ae , мұнда А-тұрақты шама.

Соңғы екі өрнек қаныққан буды идеал газ деп қарастырғанда ғана орындалады.

20. Гелий күйлердің диаграммасы

Дата добавления: 2015-06-04