Электростатика. Доставка до курьерской и транспортной компании бесплатна

Доставка до курьерской и транспортной компании бесплатна.

Доставка через транспортную компанию производится не по указанному Вами адресу, а до представительства транспортной компании в Вашем городе. При выборе этого способа доставки нельзя оплатить заказ наложенным платежом.

1З акон сохранения электрического заряда. Закон Кулона.

Электростатика – раздел электродинамики, изучающий поле неподвижных электрических зарядов. Существуют положительные и отрицательные электрические заряды. Точечный заряд – заряженное тело форма и размеры которого несущественны в данной задаче. Эл. заряд любой системы тел состоит из целого числа элементарных зарядов, равных?1,6*10^(- 19) Кл Система тел или частиц наз-ся электрически изолированной системой, если между ней и внешними телами нет обмена эл.зарядами (аналог. Тепл. Сист). Закон сохранения эл.заряда: Алгебраическая сумма эл.зарядов тел или частиц, образующих эл-ки изолированную систему не изменяется при любых процессах происходящих в этой системе. Закон Шарля Кулона: сила взаимодействия двух точечных зарядов прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (универс х-р з-н всем тяготен и з-н квадр расстояний в оптике) Силы взаимодействия равны (По III з-ну Ньютона) и направлены вдоль прямой, соединяющей заряды (Рис); 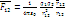где: 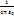коэффициент пропорциональности,?₀ - электрическая постоянная. Абсолютная электрическая проницаемость вакуума,?₀= 8,85*10^(-12) Ф/м (Кл²/Нм²). 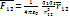Заряженные тела конечных размеров будем рассматривать, как систему точечных зарядов, тогда силу взаимодействия между такими телами рассчитывают по принципу суперпозиции.

Электрическое поле. Напряжённость поля. Принцип суперпозиции полей. Взаимодействие между электрическими заряженными частицами или телами осуществляется посредством электрического поля. Основное свойство поля: На всякий другой заряд помещённый в поле действует сила Основной силовой характеристикой эл поля является напряжённость, численно равная силе действующей на единичный положительный заряд в данной т поля. 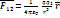- по опред Е=F/q = 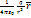Если эл поле создается несколькими точечн зарядами, тогда напряженность эл поля в каждой точке равна геом сумме полей созданных в этой точке каждым зарядом (принцип суперпозиции) Е= 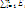Если заряженное тело протяжённое, то необходимо знать как распределены по нему эл заряды. Вводят понятия: линейной плотности заряда?= - распределении заряда по длине. поверхностной плотности заряда 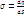- распределении заряда по поверхности. объёмной плотности заряда 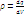- распределении заряда по объему. При непрерывном распределении зарядов результирующее поле находят интегрированным. Электрическое поле изображают с помощью силовых линий, проходящих ч/з единицу поверхности пропорционально напряженности поля в данном месте.? напряж? сил линий. Закон Кулона можно записать: F = q∙E Как только внесли заряд – в поле появляется сила. Единицей измерения напряженности является Вт/м (Н/Кл) Аvgth – в сиед для электричества. Поле называется однородным если в каждой точке напряжённость одинакова E= const

2 Потенциал и напряжённость поля диполя. Для потенциала справедлив принцип суперпозиции? = = Для поля протяженных заряженных тел ?= 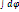= 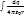, где интегрирование происходит по всем зарядам заряженного тела. Электрическим диполем называют систему из двух равных по величине и противоположных по знаку электрических зарядов +q и –q, расстояние между которыми l мало по сравнению с расстояниями до рассматриваемых точек поля. p_e = q∙l - электрический момент диполя, l – плечо диполя. Пусть l = const, по принципу суперпозиции запишем:? = 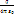(1/r₂– 1/r₁) = 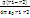(l много меньше r₁ и r₂) l <<r1,r2 r1 – r2 l cos? r1∙r2 r² (квадрату средней линии r)? = 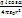, E_r = - = 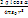E_? = Ѕ = 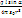(Напряженность поля диполя) E = =

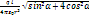3.Поле бесконечно длинной нити.

Вычислим напряженность эл поля беск нити заряженной с линейной плотностью?, на расстоянии R от нити Условно перпендик ОА=R,?. (Рис) Поле нескольких зарядов определим посредством суперпозиции, распред заряд – сумма беск малых точ зарядов. Поэтому выделим на нити бесконечно малый участок нити dl. Тогда заряд будет равным dq dq =? dl; Необходимо определить какую напряженность создает dq dE’ = Спроецируем на основное направление: {dE = dE’∙cos? {r = R/ cos?? (-?/2,?/2) 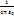=const E =

Поток вектора напряжённости. Теорема Остроградского-Гаусса в вакууме и её применение к расчёту электрических полей. В произвольном электрическом поле выделим беск-малую площадку dS, к-ю можно считать плоской. (Рис) n- нормаль к поверхности S, dS – скалярная величина. dS =n∙dS Потоком вектора напряженности сквозь поверхность dS называется величина равная: dФ = E∙cos? dS = E_n dS = 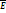d 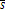Поток вектора напряженности определяет число силовых линий, проходящих, ч/з данную поверхность. Ф = 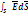Поток – скалярная величина со знаком («+» и «-») Рассмотрим поле точечного положительного заряда и окружающие его сферические поверхности. Е = En = 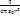по определению напряженности. (Рис) Вычислим поток вектора напряженности, ч/з эту поверхность S₂ Ф = ЕS = 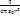4?∙r² = q/?₀. Результат остается прежним для концентрических поверхностей S₁ и S₂, для любой замкнутой поверхности, окружающей заряд q. Результат остается справедливым не только для одного заряда. Но и для любого числа зарядов, охватываемых поверхностью S. Окончательно: Ф = 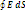= 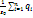- Т.Остроградского–Гаусса в вакууме: поток вектора напряженности эл поля в вакууме ч/з произвольную замкнутую поверхность, пропорционален алгебраической сумме зарядов, охватываемых этой поверхностью. Применение теоремы Остроградского-Гаусса к расчёту электрических полей. 1) Равномерно-заряженная плоскость. (Рис) 2ES = E = 2) Поле двух разноимённо заряженных плоскостей. *- погасят друг друга Е (||=|| равны по модулю и противоп по направлению) E_A = 0, E_D = 0 E_C = E= 3) Поле шара заполненного Ф = 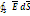= = 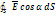=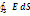E 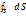=ES = E∙4?∙r² = (Рис)Заземлили большую плоскость E = Выражение остается справедливым для поля, создаваемого уединенной заряженной сферой, когда роль второго электрода играют удаленные заземленные предметы. (Рис) Внутри шара поля нет На пов-ти – максимально, обратно пропорционально падает удаляясь от пов-ти.

4. Работа в электростатическом поле. Потенциал. Эквипотенциальные поверхности. Потенциалы простейших электрических полей. Подсчитаем элементарную работу сил электростатического поля. Dr – касательная к направлению. Q – полеобразующий заряд. dA = F dr = q∙E∙dr = dA = 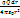- бесконечно малая элементарная работа. А₁₂ =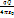 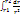= 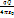(1/r₁ – 1/r₂) Поскольку результат не зависит от формы пути, а определяется электростатические силы – консервативны. Подсчитаем работу сил поля по перемещению единичного положительного заряда по произвольному замкнутому контуру (Рис) =A_1a2 + A_2b1?0 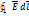=0 Циркуляция вектора напряженности электростатич поля вдоль произвольного замкнутого контураL=0; Разностью потенциалов между т. 1 и 2 называется работа, совершаемая силами поля при перемещении положительного единичного заряда из т 1 в т.2 по произвольному пути. ?₁-?₂= A=q(?₁-?₂) Физический смысл имеет только разность потенциалов между 2-мя точками, когда говорят просто о потенциале точки 2-ю т. Выбирают специально, считая либо потенциал бесконечно удаленной т. =0, либо потенциал Земли. Из A=q(?₁-?₂) следует единица измерения потенциала – 1В = 1Дж/Кл (вольт) E - напряжённость – силовая характеристика,? - - энергетическая характеристика поля. Геометрическое место точек электростатического поля, в к-х значения потенциала одинаковы называются – эквивалентной поверхностью (с одинаковым потенциалом) или эквипотенциалью. (Рис) dl ┴E?_А –?_В = 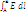=0, т.к. эквипотенциаль?_А =?_В .?_А –?_В =0,?_А =?_В =const Работа, совершаемая силами электростатического поля при перемещении эл-го заряда по одной и той же эквипотенциальной пов-ти, равна 0. Рассмотрим 2 близкорасположенные эквипотенциали с потенциалами? и? + d?. (Рис)? – (? + d?)=Edl, - d? = E∙ cos?∙ dl (dn = cos?∙ dl) E = - d? /dn? (Градиент изменения потенциала) E = - grad? d? /dn – характеризуют быстроту изменения потенциала в пр-ве. Знак “ – “ показывает, что вектор Е направлен в сторону убывания потенциала. Вычисление потенциала в простейших электрических полях. 1) Поле точечного заряда. Нет физического смысла. Разность потенциалов – часто где-то в бесконечности берут потенциал = 0?= = = =? - потенциал поля точечн заряда. 2) Сферический конденсатор Рассмотрим условн пов-ть радиуса r. Если заземлим внешнюю сферу конденсатора потенциал упадет на ней до 0. (Рис)?_r –?_a = = 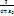(1/a – 1/r) 3) Плоский конденсатор. (Рис)? –?_x = = 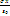?₁ –?₂ =

5 Поляризация диэлектриков. Типы диэлектриков. Диэлекриками называются вещества, к-е при обычных условиях практически не проводят эл ток. Если диэлектрик не находятся во внешнем эл поле, то сумма дипольных моментов всех мол-л, содержащихся в любом макроскопически малом объеме диэлектрика = 0 При внесении диэлектрика во внешнее эл поле происходит поляризация диэлектрика, состоящая в том, что в любом макроскопически малом его объеме возникает отличный от нуля суммарный дипольный электрический момент молекул. Диэлектрик, находящийся в таком состоянии, называется поляризованным. В зависимости от строения молекул диэлектрика различают ориентационную, электронную и ионную поляризации. Типы диэлектриков. 1) Неполярные диэлектрики, это диэлектрики, в к-х при отсутствии внешн эл поля дипольные моменты мол-л = 0, в присутствии внешнего эл поля дипольные моменты пропорциональны напряженности поля: p_e =?∙?₀ ∙E,?=4?R³ – поляризуемость атома. (Н-р, Н₂,N_2, О₂,CCl₄, бензол и др) Такие диполи называют упругими, а поляризацию деформированной (электронной). 2) Полярные диэлектрики - в таких диэлектриках дип момент не равен 0, даже при Е=0. Диполи расположены хаотично, поэтому в целом диэлектрик дипольным моментом не обладает. (Н-р, Н₂О, поливинилхлорид, спирты, пластмасса и др) Во внешнем поле на диполь действует вращающий момент (Рис) (F=qE) M = 2F sin? = q∙E∙ l ∙sin?= p_e ∙ E ∙ sin?. M = [p_e, E] – вект произвед. Если диполь находится в неоднородном поле, то он будет втягиваться в область сильного поля – ориентационная поляризация. 3) Ионные диэлектрики, - кристаллы, в к-х происходит смещение ионов разного знака в разные стороны. Электрическим моментом обладает кристалл в целом.

Дата добавления: 2015-06-04