Взаимная ёмкость двух проводников

Ёмкость проводника можно значительно увеличить, приблизив к нему другой проводник. Такая система 2-х проводников называется Конденсатором. А сами проводники – обкладками конденсатора. Такие конденсаторы состоят из 2-х металлических обкладок, расстояние между которыми мало. Тогда сообщенные проводникам заряды находятся внутри проводников (между проводниками) и созданное ими поле основательно защищено. Заряды обкладок при этом одинаковы по величине и противоположны по знаку (простой конденсатор). C = q/(?₁ -?₂) Уточним, что понимают под зарядами обкладок конденсатора (рис) Поле между пластинами такого конденсатора создается только зарядами q₂ и q₃, они противоположны по знаку q₂ = - q₃ в силу знака сохранения эл заряда: q₁+q₂ = Q₁ q₃+ q₄ = Q₂ Очевидно также, что заряды q₁ и q₄ не должны создавать поле между пластинками т.е. q₁ = q₄ Из (Ж шрифт) следует q₁ = q₄ = (Q₁+Q₂) / 2 q₂ = (Q₁–Q₂)/2 q₃ = – (Q₁ – Q₂) /2 При этом поле внутри каждой из пластинок =0 При q₁ = q₄ = 0? Q₁ = – Q₂

_8. Плоский и сферический конденсаторы.

Примеры вычисления ёмкостей. Плоский и сферический конденсаторы. 1. Плоский конденсатор состоит из 2-х параллельных металлических пластин площадью S каждая (рис) Ранее получено: ?₁ –?₂ = 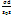?₁ –?₂ = 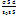C = 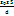2. Сферический конденсатор состоит из 2-х концентрических металлических обкладок сферической формы, радиусы которых а, b. (Рис)?_a –?_b = 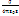(1/a – 1/b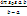) C = = C = Плоский конденсатор предельный случай сферического, когда а и в?? b-a=d, причем;d<<a d<<b Тогда: C? 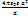? Если расстояние между обкладками достаточно мало, то независимо от их формы емкость рассчитывается по формуле C =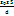

Энергия заряженного проводника и конденсатора. Сообщим уединенному проводнику заряд q. Тогда его потенциал?=q/C Станем увеличивать заряд этого проводника порциями по dq. Тогда для этого необходимо совершить работу dA = dq ∙? = q/C *dq Работа до конечной зарядки проводника от 0 до q A = 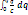= 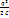Очевидно, что заряженный проводник будет обладать при этом энергией W_C = 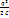= - эн-я заряженного проводника. Аналогично можно получить соотв выражение для конденсатора W_C = 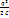= 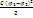Энергия конденсатора сосредоточена в его электрическом поле.

9. Энергия электрического поля. Объёмная плотность энергии.

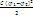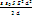Энергия электростатического поля. Объемная плотность энергии. Энергия заряженного конденсатора есть энергия поля. Рассмотрим плоский конденсатор С = - емкость,?1 –?2 = = E d W_e = = = Ѕ = Ѕ = Ѕ 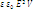,т.е. W_e пропорционально V(между обкладками) ?_e = Ѕ 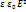?_e – объёмная плотность энергии электростатического поля. В том случае, когда поле неоднородно выражение для?_e – сохранит свою силу. dW_e =?_e dV We = 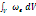Таким образом объективные св-ва электростатического поля определяются напряжённостью Е, потенциалом?, плотностью энергии?_e, а так же массой (электростат поля) Масса и энергия – есть меры объективной реальности (материи и движения) m =W_e/C², С – скорость света, т.е. поле материально, ему присущи масса и энергия.

10 Постоянный электрический ток, его свойства и характеристики. Эл ток – направленное движение эл зарядов. В неподвижном проводнике после создания в нем эл поля возникает ток проводимости. После этого проводник перестает быть эквипотенциальным, линии напряж уже не ┴ пов-ти. Два условия тока: 1. Наличие носителей заряда. 2. Электр поле. Для поддержания тока необходим источник эл-й эн-и – устройство, преобразующее какой-либо вид эн-и в эн-ю эл тока. Сила тока (ток) – скалярная физич велич I, равная отношению заряда dq, переносимого при электрич токе сквозь рассматриваемую пов-ть S за малый промежуток времени, к длительности dt этого промежутка. I = dq/dt Если величина направления тока не изменяется во времени, то он наз-ся постоянным. Для пост тока: I = q/t [I]=1A = Кл/с За направление тока условно принято направление движения положит зарядов. Если по сечению проводника ток распределен не равномерно, то вводится понятие плотности тока – отношение силы тока dI через малый элемент пов-ти ортогональной (┴ к пов-ти) направлении. Тока к плозади dS этого эл-та. j = dI / dS_┴ Можно показать, что ток I = (Рис) n – нормаль,? - угол(n,j) Если пл-ть тока всюду одинакова, то получается: I = j∙S

Законы Ома и Джоуля-Ленца в дифференциальной форме. Георг Ом экспериментально установил, то ток, текущий по однородному проводнику пропорционален разности потенциалов на концах проводника I =?₁ –?₂/R Проводимость измеряется в сименсах. Для цилиндрич проводника R=?* l /S Получим дифференциальную форму записи. Рассм цил проводник длиной dl, площ сечения ds. (Рис) Применим з-н Ома dI = j dS dR =?* dl / dS d?= E dl j∙dS = 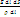j = E /? (?=1/? –удельная проводимость) j = E/? =?∙E j?? E – сонаправлены j =?∙E - диф-я ф-ма записи з-на Ома (Справедливо в любой т проводника) Известен з-н Джоуля-Ленца: Q = I² ∙R∙t dQ = j²∙dS²∙?∙(dl /dS) ∙ dt ώ= 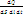=?E² – объемн пл-ть тепловой эн-и ώ =?E² – з-н Джоуля-Ленца в диф ф-ме. Т.е. тепло, выделяемое в единице объема проводника в единицу времени пропорционально квадрату напряженности эл поля. ώ~Е

Сторонние силы. Обобщённый закон Ома. Действие только Кулоновских сил электростатич поля не обеспечивает наличие постоянного тока. В цепи постоянно должны действовать т наз. сторонние силы неэлектрическ происхожд, к-е непрерывно разделяли бы заряды. Н-р, гальванические эл-ты, аккумуляторы и т.д. засчет поля сторонних сил внутри источника эн-и эл-е заряды постоянно движутся против Кулоновского поля. На концах цепи поддерживается постоянная разность потенциалов. Обозначим напряженность поля Кул сил Е, а поле сторонних сил Е_СТОР. Пусть электр цепь такова, что в любых точках произвольного перпендикулярного к проводнику сечения S величины E, E_СТОР,? и j. Обобщим з-н Ома для этого случая: j =?(E+E_СТОР) Умножим скалярно л. и п. части этого выраж на?∙dl (?=1/?) ?∙j∙d l = Ed l +E_СТОРd l Проинтегрируем это выражение на участке от т 1 до т 2.I= 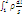= = R – полное электрич сопрот уч цепи. 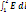=?₁ –?₂ =? - ЭДС U = I∙R =?₁ –?₂ +? - Обобщ з-н Ома для уч цепи в интегральн ф-ме. Величина ?₁ –?₂ +? = U - Электрич напряжение. Если цепь замкнута, то ?₁ –?₂ =0, тогда U =? U= I∙R.

Разветвлённые цепи. Правила Кирхгофа. На практике приходится рассчитывать сложные и разветвленные цепи пост тока. Решение таких задач обеспечивается использованием 2х правил Кирхгофа. Узел цепи - т, в к-й сходится 3 и более тока. При этом считают подходящие токи положительными, а отходящие отрицательными. 1 правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле = 0. (Рис) i₁+i₂ –i₃ =0 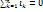-обобщ прав Кирхгофа. Выделим мысленно в разветвленной цепи произвольный контур к к-му применим обобщ з-н Ома. (Рис) Напр обх контура выберем по часовой стрелке. При выбранном направлении обхода перед? ставится знак +, если осуществляется переход от отрицат полюса к положительному (- | ├) i₁R₁=?_A –?_B +?₁; i₂R₂=?_B –?_C -?₂; i₃R₃=?_C –?_A -?₃ (сложим эти ур-я) i₁R₁ + i₂R₂+ i₃R₃=?₁ -?₂ -?₃ - 2е правило Кирхгофа: В любом замкнутом контуре произвольно выбранном в разветвл электрич цепи алгебраическая сума произведений токов на сопротивления соответствующих уч-ков этого контура = алгебр сумма? (ЭДС) в этом контуре.

11. Классическая электронная теория металлов. Вывод законов Ома и Джоуля-Ленца из электронных представлений. Электронная теория объясняет различные св-ва в-ва, существованием и движением в них электронов. В этой теории движение эл-нов подчиняется з-нам классической механики Ньютона. Взаимодействием эл-нов пренебрегают, учитывая соударение эл-нов с узлами крист решетки металлов. Т.е. эл-ны уподобляют идеальному газу в молек физике. Поэтому можно говорить о средней длине свободного пробега эл-нов –?, к-я по порядку величины = 10 ^(- 8) см (1 анстрем = 10 н м) Для средней кинетич энергии теплового движения эл-нов можно записать: Ѕ m с² = kT, с – средняя квадратичн ск-ть (t=0, c? 100 км/с) Таков же порядок и средней арифм ск-ти u. Поскольку тепловое движение эл-нов хаотично – оно не приводит к возникновении. Эл тока. Под действием внеш поля Е возникает упорядочен движ эл-нов и электрич ток. j = n∙e∙V, j – пл-ть тока, n – концентрация. (Рис) оценка V дает рез-тат = 8* 10^(- 4) м/сV<<u(сред арифм) Пусть в проводнике создано эл поле напряженностью Е. тогда на кажд эл-н действует сила F = e∙E Ускорение: a = e∙E/ m = F/m За время свободного пробега? =?/u он набирает ск-ть V_? = a∙? = 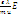V = = 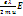Тогда пл-ть тока j: j= 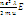,? = - проводимость j =?E – з -н Ома в диф ф-ме Подсчитаем эн-ю W, к-ю приобретает под действием поля эл-н за время t. W = = = = ,? - время своб пробега. Тогда для пл-ти теплов мощн-ти? = = ? =?E² – з-н Джоуля-Ленца.

Дата добавления: 2015-06-04