Параллельное проецирование

Можно, однако, достигнуть того, что изображение будет по величине равно самому предмету. Для этого надо предположить, что на предмет смотрят издалека или проецируют его лучами из бесконечно далекой точки, например солнечными лучами. Тогда углы между проецирующими лучами будут так малы, что лучи можно считать параллельными. В этом случае проецирование называется параллельным. При этом методе проецирования величина проекции не будет зависеть от расстояния; она не будет зависеть и от того, где разместится экран — за изображаемым предметом или перед ним.

Параллельным проецированием нами были получены тени пресс-папье в уроке "Что такое проекция фигуры на плоскость?" на рисунке 5.

На рисунке 3 и 4 приведен другой пример, поясняющий способы центрального и параллельного проецирования.

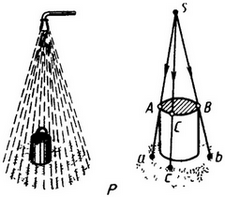Рис. 3. Способ центрального проецирования

Рис. 4. Способ параллельного проецирования

Одно ведро, вверху, поставлено под душ, а другое такое же, внизу,— под отвесный дождь. Если через некоторое время убрать ведра, то мы обнаружим, что верхнее ведро оставило сухое пятно большого диаметра, а нижнее — равное диаметру ведра. Сухие пятна есть не что иное, как проекции ведер, полученные вверху методом центрального проецирования, а внизу — методом параллельного проецирования. Проецирующими лучами в данном случае являлись струйки воды.

Центральное проецирование находит широкое применение главным образом в живописи, в архитектурных проектах при изображении зданий и сооружений.

В этом случае центральные проекции называют линейной перспективой. Пример изображения здания в перспективе дан на рисунке 5.

Рис. 5. Здание в перспективе при центральном проектировании

Вернемся к рисунку 4. На нем изображен случай, когда капли дождя падают строго вертикально, под прямым углом к поверхности земли. Такие параллельные проекции называются прямоугольными.

Но представьте себе, что начался сильный ветер и капли дождя стали падать на землю под острым углом.

Сухое пятно на этот раз изменило форму: оно перестало быть круглым (рис. 6). Чем острее угол, тем более вытянутой будет проекция ведра. Такие проекции называются косоугольными.

Рис. 6. Косоугольная проекция

Прямоугольные и косоугольные проекции обычно применяются для выполнения чертежей и технических рисунков. Теперь давайте подумаем, так ли уж сложны принципы, из которых исходит сложная наука об изображении на бумаге объемных тел? При внимательном чтении мы видим, что принципы эти просты и целиком заимствованы из окружающей нас действительности.

Мы лишь воспроизводим на бумаге те процессы, которые совершаются реально в самой природе.

Если на ведре наметить некоторую точку А (см. рис. 3), то о ней можно сказать, что она проецируется из точки S в точку а плоскости Р.

Здесь точка А — оригинал; а — проекция оригинала; прямая Аа — проецирующая прямая (проецирующий луч); плоскость Р — плоскость проекций.

То же самое можно сказать о точках В, С и всех остальных точках оригинала.

Отсюда легко сделать вывод: чтобы спроецировать какое-либо тело на плоскость, нужно спроецировать на плоскость все его точки.

На рисунке 4 нет точки S. Проецирующие лучи идут параллельно между собой и перпендикулярно к плоскости проекций. В этом случае можно сказать, что прямоугольной проекцией точки А на плоскость Р будет основание а перпендикуляра Аа, опущенного из точки А на плоскость Р. Это обстоятельство нужно твердо запомнить, так как нам придется им пользоваться при знакомстве с прямоугольными проекциями.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ точки

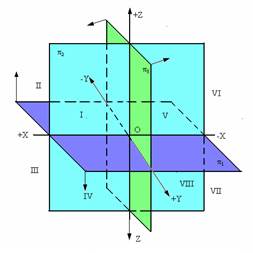Так называемые правила построения изображений на эпюрах базируются на методе проекций. 1-о изображение реального тела не дает знать о его реальной форме или форме простейших геометрических образов, делающих это изображение. Итак, нельзя знать о положении точки в пространстве по 1 ее проекции; положение точки в пространстве определяется 2мя проекциями.

Посмотрим на пример построения проекции точки А, расположенной в пространстве 2-х гранного угла (рис.)

Сделанный эпюр назовем комплексным чертежом.

Это изображение предмета на нескольких (ДВУХ, ТРЕХ) совмещенных плоскостях.

Комплексный чертеж, состоит из 2х ортогональных проекций, связанных между собой - двухпроекционный.

На этом чертеже горизонтальная и фронтальная проекции точки лежат на 1-ой вертикальной линии связи.

Три координатные плоскости проекций образуют четыре пространственных угла – октанта (в общем случае – 8 октантов).

Для упрощения дальнейших рассуждений будем рассматривать только часть пространства, расположенную влево от профильной плоскости проекций

Прямоугольное (ортогональное) проецирование на одну плоскость проекций

В промышленности весьма широко используются так назы­ваемые плоские детали (пластины, уголки, прокладки, решетки, лекала швейного и обувного производств и т. д.), имеющие про­стую или сложную конфигурацию при незначительной толщине самих деталей (рис. 53). Для отображения их на чертеже доста­точно построения одной проекции. Как вы уже знаете, при прямоугольном проецировании на од­ну плоскость проекций деталь следует расположить таким образом, чтобы полученное изображение давало наибольшую инфор­мацию о ее форме (рис. 54). 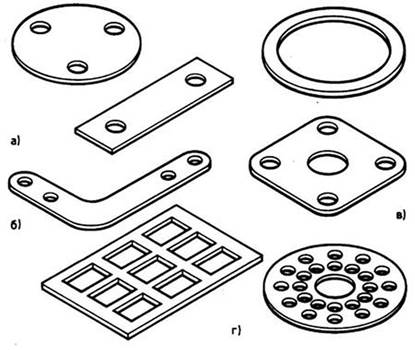Рис. 53. Плоские детали: а — «Пластины»; б — «Уголок», в — «Про­кладки»; г — «Решетки» 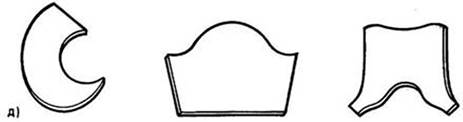Рис. 53. Продолжение: д — лекала кроя Рис. 54. Расположение детали относительно плоскости проекций: а — правильное расположение; б — неправильное расположение; в — про­цесс и результат проецирования   Выберем для получения изображения вертикальную (фрон­тальную) плоскость проекций (К). Перед ней мысленно располо­жим деталь «Уголок» (рис. 54, в) так, чтобы формообразующая грань стала параллельно плоскости проекций. В результате прямоугольного (ортогонального) проецирования получим изо­бражение детали, на котором грани предмета, параллельные плоскости проекций, отобразятся в натуральную величину. Боко­вые грани, перпендикулярные плоскости проекций, спроецируются в отрезки прямых. Ребра, параллельные фронтальной плоскости проекций, изобразятся в натуральную величину, а ребра, перпендикулярные ей, — в точки. Цилиндрические отвер­стия «Уголка» спроецируются в виде окружностей. Полученное изображение называется фронтальной проекцией. Эта проекция содержит основную информацию о форме детали, воспроизводит ее контур, дает представление о высоте и длине, не передавая при этом толщину или ширину. Информацию об этих величинах на некоторых деталях (малой толщины или изготовленных из профиля проката — уголок, тавр, швеллер, рельс) показывают с помощью знака толщины — «s» с указанием соответствующего размера (не более 5 мм) или знака длины «l», например l 200 (рис. 55). Проекции не содержат информацию о материале и цвете предмета. В дизайнерских проектных чертежах допускается показывать цвет предмета на прямоугольных (ортогональных) проекциях. Для выбора рационального способа построения чертежа лю­бой плоской детали необходимо проанализировать форму, вы­явив ее особенности. Форма бывает симметричной и несиммет­ричной (асимметричной). От этого зависит последовательность 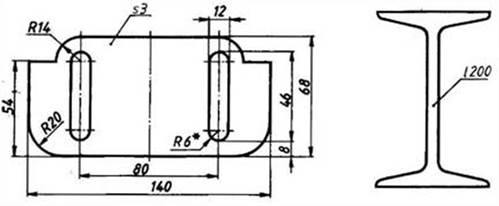Рис. 55. Чертежи плоских деталей с обозначением толщины и длины Рис. 56. Последовательность построения проекции несимметричной (а) и симметричной (б) деталей 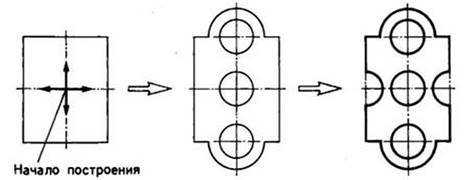  Рис. 57. Последовательность построения проекции детали, имеющей две оси симметрии   построения изображений. На рисунке 56 показана последова­тельность построения фронтальных проекций плоских деталей несимметричной и симметричной формы. Если деталь симметрична и имеет две оси симметрии, то по­строение изображения формы детали ведется от точки пересе­чения осей симметрии в последовательности, показанной на ри­сунке 57. 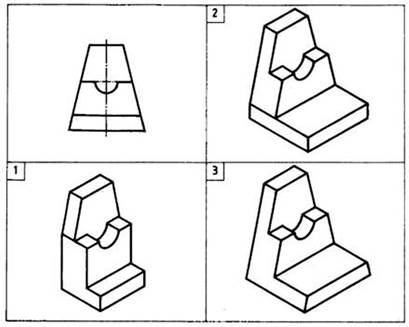Рис. 58. Определение соответствия чертежа и наглядного изображения многоугольника ABCD, расположив его относительно плоскости проекций Н: а) параллельно; б) перпендикулярно; в) наклонно. Назовите стороны прямоугольника, которые отобразились на плоскость H с искажением; в натуральную величину; в точку. 3. Определите соответствие чертежа и наглядного изображения (рис. 58)

Дата добавления: 2015-06-29