Лекция №15

Начертить на миллиметровой бумаге с заполненной основной надписью и принести в ПОРТФОЛИО(папка с файлами)

Февраля

Практическое занятие Прямоугольное проецирование на две взаимно перпендикулярные плоскости проекций (метод Монжа). Проецирование на три взаимно перпендикулярные плоскости проекций. (1) Гл. 1 п.2.1-2.2; (2) Гл.11-13.

Провести построение тела (пирамида) с проекцией точек на всех 3 плоскостях, по 3 варианту, как в самостоятельной №8

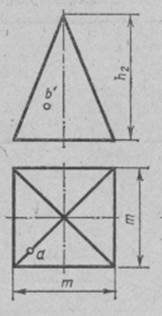
20 февраля

Практическое занятие Положение прямой относительно плоскостей проекций. Взаимное расположение точки и прямой Определение натуральной величины отрезка. (1) Гл. 1 п.2.1-2.2; (2) Гл.11-13.

Конспектируем курсив и чертежи в тетрадь (переносим рисунки все модель, эпюр, цветными карандашами чертить отрезки)

ПОЛОЖЕНИЕ ПРЯМОЙ ЛИНИИ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

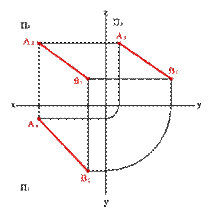
1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.1).

а) модель	б) эпюр
Рисунок 1. Прямая общего положения

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:

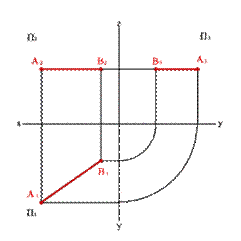
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.2).

а) модель	б) эпюр

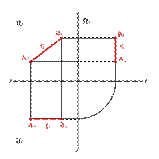
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями (рис.3).

а) модель	б) эпюр
Рисунок 3. Фронтальная прямая

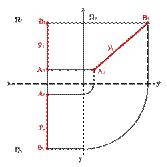
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 4).

Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.

а) модель	б) эпюр
Рисунок 4. Профильная прямая

3. Прямые перпендикулярные плоскостям проекций, занимают частное положение в пространстве и называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:

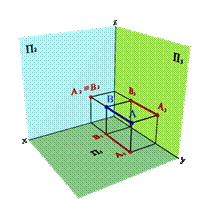
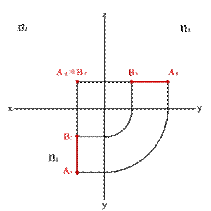
3.1. Фронтально проецирующая прямая - АВ (рис. 5)

а) модель	б) эпюр
Рисунок 5. Фронтально проецирующая прямая

3.2. Профильно проецирующая прямая - АВ (рис.6)

а) модель	б) эпюр
Рисунок 6. Профильно-проецирующая прямая

3.3. Горизонтально проецирующая прямая - АВ (рис.7)

	а) модель	б) эпюр
	Рисунок 7. Горизонтально-проецирующая прямая
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ И ПРЯМОЙ

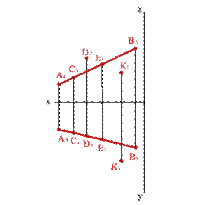
Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке 8 точек, только одна точка С лежит на прямой АВ.

а) эпюр	б) модель
Рисунок 8. Взаимное расположение точки и прямой

В тех случаях, когда точка и прямая лежат в плоскости уровня (параллельной какой-либо из плоскостей проекций П ₁, П ₂ и П ₃), то вопрос о взаимном расположении прямой и точки решается при построении проекций на плоскость соответственно П ₁, П ₂ или П ₃. Например, прямая АВ и точка К лежат в плоскости параллельной профильной плоскости проекций (рис.9).

Из свойств параллельного проецирования известно, что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же соотношении.

Зная это условие можно определить принадлежность точки К прямой АВ:

А₂К₂ /К₂В₂ ¹А₁К₁/К₁В₁ Þ КÏАВ

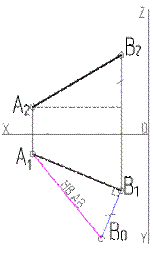
Определение натуральной величины отрезка.
Имея две проекции прямой частного положения мы всегда можем определить натуральную величину любого отрезка отложенного на этой прямой. Для этого используется метод прямоугольного треугольника.

вы должны знать, что построить прямоугольный треугольник мы можем как на горизонтальной, так и на фронтальной плоскостях. Это показано на рисунке 1 ниже - на нем мы сначала определили натуральную величину АВ на горизонтальной плоскости проекции, а затем на фронтальной

Коротко же алгоритм определения натуральной величины отрезка сводится следующему: на любой проекции через любую из конечных точек отрезка проводят перпендикулярную прямую, и на ней откладывают расстояние, равное разнице значений по оси ординат этих двух точек на противоположной плоскости проекций. Т.е. если треугольник строим на горизонтальной плоскости, то разницу значений ищем на фронтальной, и наоборот. Если что-то непонятно из этого описания, то рассмотрев внимательно рисунок вы окончательно поймете, что имелось ввиду.

Как видите, ничего особо сложного в этом приеме нет, но знать его очень важно, и не менее важно уметь его применить, как минимум до получения зачета по начертательной геометрии и инженерной графике:)

Особым случаем этой задачи является определение натуральной величины отрезка лежащего в частном положении - например параллельно горизонтальной плоскости проекции. Тогда на его горизонтальная проекция будет сама по себе натуральной величиной и никаких дополнительных построений для ее определения не требуется:

Дата добавления: 2015-06-29