Теоретическое введение

Цель работы

Изучение температурной зависимости электропроводности полупроводников

Лабораторная работа 6.8

Изучить зависимость электропроводности полупроводникового образца от температуры. Определить ширину запрещенной зоны

Электропроводность 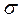материалов определяется выражением:

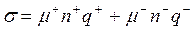(1)

где q⁺ и q^- -соответственно величина заряда положительных и отрицательных носителей электрического заряда, n⁺ и n^-- концентрация соответственно положительных и отрицательных носителей заряда, µ⁺ и µ^- подвижности положительных и отрицательных носителей заряда.

В нашей задаче исследуется собственная электропроводность полупроводника. Поэтому положительными носителями заряда являются дырки, а отрицательными - электроны. Следовательно,

І q ⁺І= І q ^-І= e

и, поскольку полупроводник собственный, то n⁺= n^-= n

Тогда 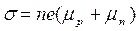(2)

Здесь µ_n и µ_p- подвижность электронов проводимости и дырок, соответственно.

Строго говоря, от температуры зависят и концентрация, и подвижности носителей заряда. Однако во многих случаях в узком диапазоне температур зависимостью подвижностей от температуры можно пренебречь и считать подвижности постоянными, не зависящими от температуры. В данной работе рассматривается именно этот случай.

Зависимость концентрации собственных носителей от температуры описывается экспонентой:

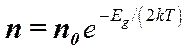(3)

Здесь E_g- ширина запрещенной зоны, k - постоянная Больцмана, T- температура образца, n₀- концентрация носителей при высоких температурах.

Отсюда (4)

Обозначим n₀ e(µ_n+µ_p)= и условно назовем это электропроводностью образца при бесконечно большой температуре. В результате получим выражение для электропроводности образца:

(5)

Таким образом, зависимость электропроводности собственного полупроводника от температуры является экспоненциальной. Уравнение (5) поддается экспериментальной проверке и позволяет определить ширину запрещенной зоны полупроводника E_g. Именно это и является целью данной лабораторной работы.

Прологарифмируем формулу (5). Получим:

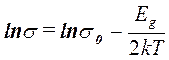(6)

Отсюда следует, что график зависимости 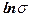от 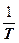представляет собой прямую линию, что легко проверить практически. Для вычисления ширины запрещенной зоны E_g поступим следующим образом. Построим прямую (6). В уравнении (6) имеем два неизвестных: ширину запрещенной зоны E_g и логарифм электропроводности при бесконечно большой температуре lns ₀. Возьмем на прямой (6) две произвольные точки. Уравнение (6) для этих точек запишется как

(7)

Решив эту систему относительно E_g, получим:

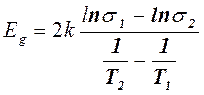(8)

Формула (8) является рабочей для вычисления ширины запрещенной зоны полупроводника.

В данной работе полупроводниковый образец выполнен в виде

параллелепипеда, имеющего длину l, ширину a и высоту b. Для вычисления электропроводности образца воспользуемся законом Ома. Электрическое сопротивление образца по закону Ома равно

(9)

где U- электрическое напряжение на образце, I- сила тока через образец. Приняв во внимание геометрию образца и связь электропроводности и удельного сопротивления 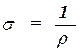, найдем выражение для электропроводности полупроводникового образца

(10)

где S=ab - площадь поперечного сечения образца.

Дата добавления: 2015-06-29