Расчётно-графическая работа №3: Геометрические характеристики плоских сечений

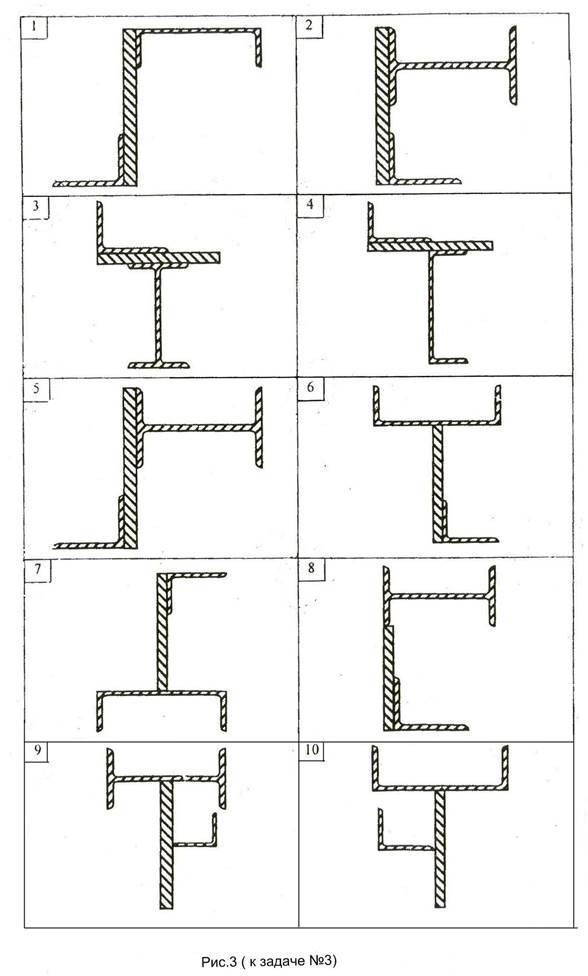
Для заданного сечения (рис.3), состоящего из трех фигур (прокатных профилей): уголка(№1); двутавра(№2) (или швеллера); полосы(№3) определить:

1. Положение главных центральных осей инерции.

2.Вычислить главные центральные моменты инерции сечения. Данные, необходимые для решения задачи, выбрать из таблицы вариантов (Табл.3). Геометрические характеристики прокатных профилей можно найти в приложении 4 (таблицы с 1 по 4) сборника заданий по сопротивлению материалов или справочниках и учебниках по сопротивлению материалов, например в [1],[2],[3] из списка литературы.

Указания к выполнению работы

1. Заданное сечение вычерчивается в стандартном масштабе на листе формата A4.

2. На чертеже сечения показывается положение главных центральных осей. сечения.

3. На чертеже сечения обозначается также положение первоначальных осей, собственных центральных осей отдельных частей сечения, расстояния и углы между осями в общем и числовом виде.

4. Шаблон таблицы результатов приводится ниже (таблица 4), в неё должны быть сведены результаты вычислений.

Таблица 3

№ варианта	Уголок	Швеллер или двутавр	Полоса bxh
	4(4)		10х160
	5(4)		20х100
	11(8)		10х200
	7(6)		8х160
	4,5(4)		6х100
	12,5(10)		20х200
	14(8)		40Х400
	4(4)		6х120
	14(10)		15х300
	7(6)		30х100
	4/2,5(5)		10х100
	8/5(6)		25х100
	7/4,5(5)		10х150
	20/12,5(14)		50х250
	11/7(8)		16х100
	14/9(10)		10х250
	20/12,5(11)		40х400
	7(6)		6х120
	7(6)		15х150
	7/4,5(5)		10х100
	11(8)		20х100
	8/5(6)		10х200
	4,5(4)		8х160
	5/3,2(4)		6х100
	11/7(8)		20х200
	20(16)		50х250
	4/2,5(4)		16х100
	12,5(10)		10х250
	20/12,5(14)		40х400
	7/4,5(5)		6х120

В скобках указана толщина полок уголка в мм.

Вопросы для защиты расчетно-графической работы №3

1. Что называется статическим моментом сечения относительно оси, какова его размерность.

2. Какова связь между статическими моментами относительно двух параллельных осей.

З. Чему равен статический момент относительно центральный оси.

4. Как определяются координаты центра тяжести простого и сложного сечений.

5. Что называется осевым, полярным и центробежным (смешанным) моментами инерции, какова их размерность и свойства.

6. Выведите формулы для определения осевых моментов инерции прямоугольника, треугольника и круга относительно центральных осей.

7. Чему равны полярные моменты инерции круга и кольца относительно центральных осей.

8. Какова зависимость между моментами инерции относительно параллельных осей, если одни из них центральные.

9. Как изменяются моменты инерции относительно центральных осей при их повороте.

10. Какие оси называются главными центральными осями инерции сечения. Какие осевые моменты инерции называются главными, каким свойством они обладают.

11 Чему равен центробежный момент относительно главных осей инерции.

12. Какие геометрические признаки сечения позволяют определять положение главных осей инерции.

13. Порядок вычисления главных моментов инерции сложного сечения.

14. Как изменяются значения моментов инерции правильных фигур (круг, квадрат равносторонний треугольник и т.д.) относительно взаимно перпендикулярных центральных осей при повороте их на произвольный угол.

Дата добавления: 2015-06-30