Вторая теория прочности (теория наибольших линейных деформаций)

Первая теория прочности (теория наибольших нормальных напряжений).

Согласно этой теории, выдвинутой Галилеем (XVII в.), преимущественное влияние на прочность оказывает величина наибольшего нормального напряжения.

Нарушение прочности в общем случае напряженного состоянии наступает тогда, когда наибольшее нормальное напряжение достигает опасного значения (s₀). Последнее легко устанавливается при простом растяжении на образцах из определённого материала.

Условие нарушения прочности при сложном напряженном состоянии имеет вид

s₁=s₀.

Следовательно, условие прочности с учетом коэффициента запаса n будет

s₁£[s], (85)

где

[s]= .

Таким образом, первая теория прочности из трех главных напряжений учитывает лишь одно – наибольшее, полагая, что два других не влияют на прочность.

Опытная проверка показывает, что эта теория прочности непригодна для большинства материалов и дает, в общем, удовлетворительные результаты лишь для весьма хрупких материалов.

Согласно второй теории прочности, предложенной Мариоттом (1682г.), принимается в качестве критерия прочности наибольшая по абсолютной величине линейная деформация. По этой теории нарушение прочности в общем случае напряженного состояния наступает тогда, когда наибольшая линейная деформация e_max достигает своего опасного значения e₀. Последнее определяется при простом растяжении образцов из определённого материала.

Таким образом, условия разрушения и прочности соответственно будут:

e_max=e₀,

e_max£[e]= 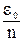. (86)

Используя обобщенный закон Гука, легко выразить условие прочности в напряжениях:

e_max=e₁= 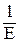[s₁-m(s₂+s₃)].

При простом растяжении, приняв в качестве допускаемого напряжения [s], мы тем самым для наибольшего относительного удлинения допускаем величину

[e]= .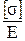

Подставляем выражения для e_max и [e] в (86) и находим:

[s₁-m(s₂+s₃)] £ [s]. (87)

Опытная проверка этой теории также показала, что она неприменима для большинства материалов и дает удовлетворительные результаты лишь для хрупкого состояния материала (например, легированный чугун, высокопрочные стали после низкого отпуска). Отметим также, что применение второй теории прочности в виде (87) недопустимо для материалов, не подчиняющихся закону Гука, или за пределами пропорциональности, а также когда наибольшая по абсолютной величине деформация отрицательна.

Дата добавления: 2015-06-30