Касательные напряжения при кручении

Задачу по определению касательного напряжения при кручении будем решать с использованием двух гипотез:

- гипотеза плоских сечений;

- радиус, проведенный в сечении до деформации, не искривляется в процессе деформации.

Рассмотрим стержень, нагруженный крутящим моментом. На некотором расстоянии z от начала стержня вырежем бесконечно малый элемент dz (рис.34).

Рис.34

Рассмотрим статическую сторону задачи. Для этого найдем связь между крутящим моментом в сечении (рис.35) и касательным напряжением. Любой момент - это произведение силы на плечо. В данном случае для элементарного крутящего момента сила - это произведение касательного напряжения на площадь, на которой оно действует, а плечо есть радиус-вектор от центра тяжести сечения до рассматриваемой точки.

Рис.35

М_к = 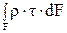(76)

Теперь рассмотрим вырезанный элемент dz (рис.36) с геометрической стороны. В процессе нагружения правое сечение повернется по отношению к левому на некоторый угол dφ. Отрезок АВ после деформации занял положение АВ₁.

Рис.36

Найдем длину дуги ВВ₁ из треугольников АВВ₁ и ОВВ₁:

dz×g = r×dφ

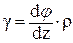(77)

С физической точки зрения при сдвиге справедлив закон Гука.

t = g×G (78)

Подставим угловую деформацию из геометрического соотношения (77) в закон Гука (78):

t = 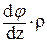×G (79)

Полученное выражение подставим в формулу (76):

М_к = ,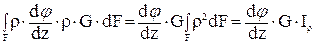

= .

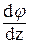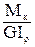сделав подстановку в выражение (77), получим:

,

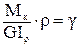полученное выражение подставляем в закон Гука (78):

t = 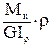×G.

Окончательно получаем формулу для расчета касательных напряжений в сечении при кручении:

t = 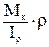(80)

Таким образом, касательные напряжения при кручении круглого стержня распределяются по линейному закону и достигают своего максимума на периферии сечения.

Дата добавления: 2015-06-30