Вопросы для самопроверки. 1. Что называется рамой, фермой?

1. Что называется рамой, фермой?

2. Как определить степень статической неопределимости рамы?

3. Каковы преимущества и недостатки статически неопределимых систем?

4. Что такое основная система?

5. Какие способы раскрытия статической неопределимости вы знаете?

6. В чем сущность метода сил?

7. Что физически выражает каноническое уравнение метода сил?

8. Что физически выражают коэффициенты канонических уравнений?

9. Как определяются коэффициенты канонических уравнений?

10. Как проверяется правильность коэффициентов канонических уравнений?

11. Как строятся эпюры внутренних силовых факторов в рамах?

12. Как проверяется правильность построенных эпюр внутренних силовых факторов?

13. Как проверяется правильность построения эпюры изгибающих моментов в статически неопределимой раме с точки зрения кинематики? Что физически означает эта проверка?

14. Как упрощается система канонических уравнений для симметричных рам?

15. Каков смысл введения групповых неизвестных?

16. Как определяются перемещения при изгибе в рамах?

7. РАСЧЕТ ПРОСТРАНСТВЕННЫХ СИСТЕМ НА ПРОЧНОСТЬ
ПРИ СЛОЖНОМ СОПРОТИВЛЕНИИ

Построение эпюр внутренних силовых факторов. В конструкциях встречаются стержни, оси которых не лежат в одной плоскости, а также плоские системы, находящиеся под действием пространственной нагрузки (раздел 4, рис. 4.1). В поперечных сечениях таких систем могут действовать все шесть внутренних силовых факторов: продольная, поперечные силы, крутящий и изгибающие моменты [1 – 11]. Данный вид деформаций называется сложным сопротивлением. Для расчета на прочность при сложном сопротивлении необходимо вначале построить эпюры всех внутренних силовых факторов. Эпюры строятся методом сечений по участкам, при выборе которых необходимо руководствоваться правилами, изложенными в разделах 1 – 4. При замене отброшенной части шестью внутренними силовыми факторами они направляются в соответствии с правилами знаков, также приведенными в предыдущих разделах. Для определения искомых внутренних силовых факторов составляются уравнения равновесия пространственной системы сил (см. далее задачу 7).

Расчет на прочность. Так как в сечении элемента при сложном сопротивлении одновременно действуют шесть внутренних силовых факторов, лежащих в разных плоскостях, то в различных точках сечения также одновременно возникают как нормальные, так и касательные напряжения, поэтому расчет на прочность ведется по эквивалентным напряжениям. В качестве примера рассмотрим элемент круглого поперечного сечения.

Наибольшие напряжения изгиба возникают в точках k и 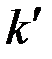, наиболее удаленных от нейтральной оси (рис. 7.1), они определяются по формуле:

,

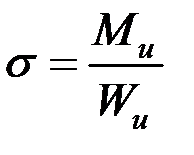где 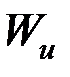– момент сопротивления при изгибе (см. раздел 3).

В этих же точках имеют место и наибольшие касательные напряжения кручения (см. раздел 2):

,

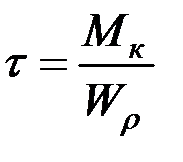где 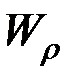– момент сопротивления при кручении.

Рис. 7.1. Напряженное состояние вала: а) эпюры напряжений;
б) распределение напряжений

Как следует из рис. 7.1, напряженное состояние является упрощенным плоским (сочетание одноосного растяжения и чистого сдвига) [1 – 7]. Если вал выполнен из пластичного материала, оценка его прочности должна быть произведена по одному из критериев текучести. Например, по III теории прочности (критерий Треска – Сен-Венана) эквивалентные напряжения определяются по формуле:

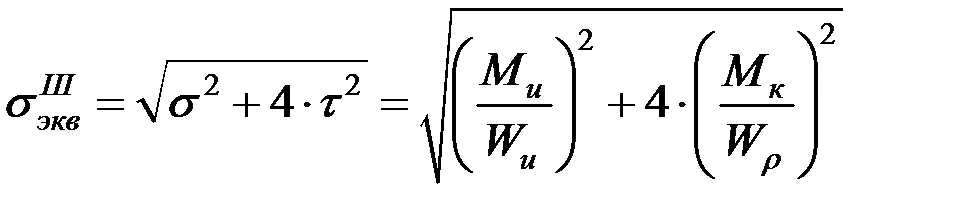. (7.1)

Учитывая, что 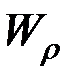=2 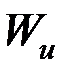, для эквивалентных напряжений получаем:

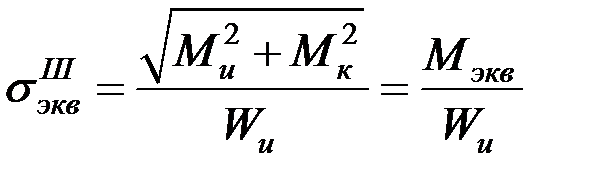, (7.2)

где 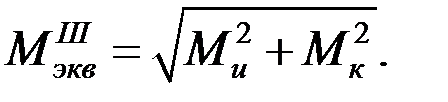(7.3)

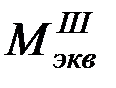– эквивалентный момент, вычисленный в соответствии с третьей теорией прочности, с введением которого задача расчета на совместное действие изгиба и кручения, сводится к расчету на эквивалентный изгиб.

Аналогично по IV теории прочности (критерий Губера – Мизеса – Генки) для М_экв получаем:

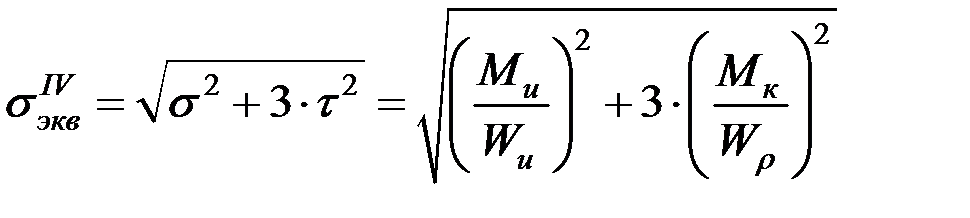, (7.4)

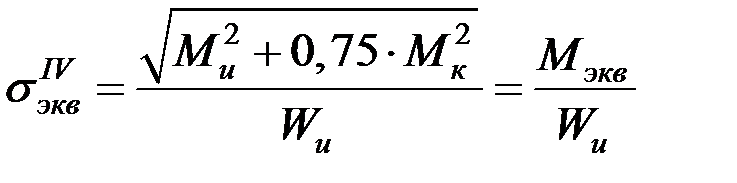, (7.5)

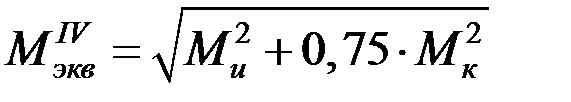. (7.6)

Таким образом, обобщая вышесказанное, условие прочности для элемента, выполненного из пластичного материала, будет иметь вид:

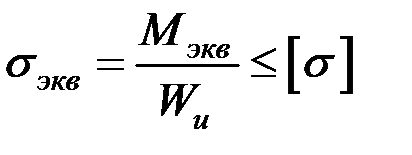, (7.7)

где 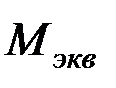определяется либо по третьей, либо по четвертой теории прочности.

Для стержня из хрупкого материала условие прочности следует записать в виде:

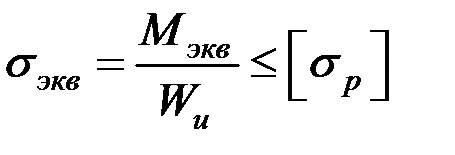, (7.8)

где М_экв должен быть записан применительно к одному из критериев хрупкого разрушения. Например, по критерию Мора [1 – 11]:

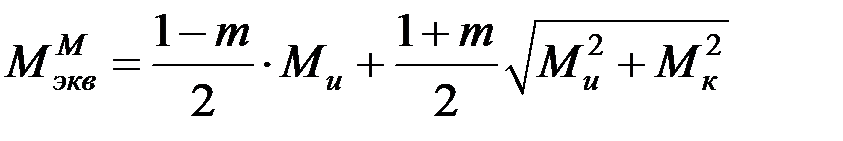, (7.9)

где .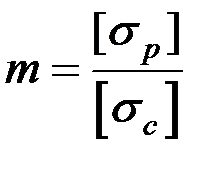

Обратим внимание на особенности расчета при сочетании изгиба, растяжения и кручения стержня прямоугольного поперечного сечения (рис.7.2.). Для выявления опасной точки здесь должны быть сравнены напряжения косого изгиба с растяжением в точке А с эквивалентными напряжениями в точках В и С.

Рис. 7.2. Модель расчета напряжений при сочетании кручения,
растяжения и изгиба

ЗАДАЧА 7

Необходимо построить эпюры внутренних силовых факторов и определить диаметр поперечного сечения, считая его постоянным на всех участках.

Дано: схема рамы приведена на рис. 7.3, где Р₂ = 20 кН, Р₃ = 40 кН,

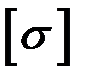=160 МПа.

Рис. 7.3. Построение эпюр внутренних силовых факторов
при сложном сопротивлении

Решение

Дата добавления: 2015-06-30