
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Раскрытие статической неопределимости рамы
|
|
|
|
Составление системы канонических уравнений метода сил.
Выбор основной системы.
Определение степени статической неопределимости рамы.
Степень статической неопределимости рамы определяем по формуле:
S = n – 3 = 5 – 3 =2 – рама дважды статически неопределима.
Выбираем основную систему: удаляя опору в точке F (рис. 6.6, а). Изображаем эквивалентную систему (рис. 6.5, б).
Составляем канонические уравнения метода сил. Для дважды статически неопределимой системы они имеют вид [1–3,5–7, 9, 11]:
 ,
,

4.1. Определение коэффициентов системы канонических уравнений метода сил.
Для определения коэффициентов  изображаем два единичных состояния основной системы и строим две единичные эпюры
изображаем два единичных состояния основной системы и строим две единичные эпюры  и
и 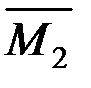 (рис. 6.6, а–в; 6.7, а).
(рис. 6.6, а–в; 6.7, а).
Коэффициенты определяем перемножением единичных эпюр по методу Мора–Верещагина [1–3,5–7, 9–11, 14–17]:
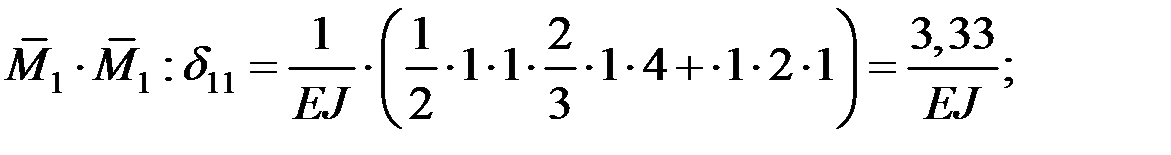
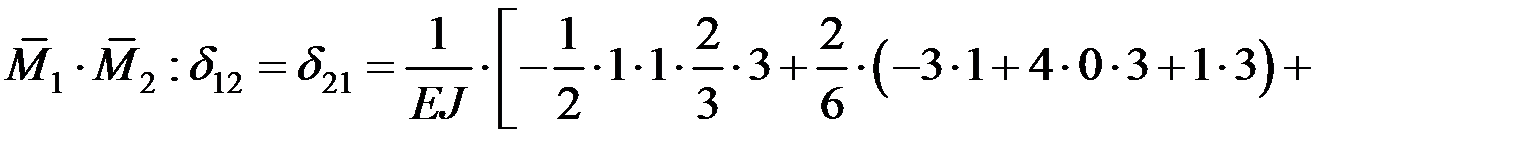

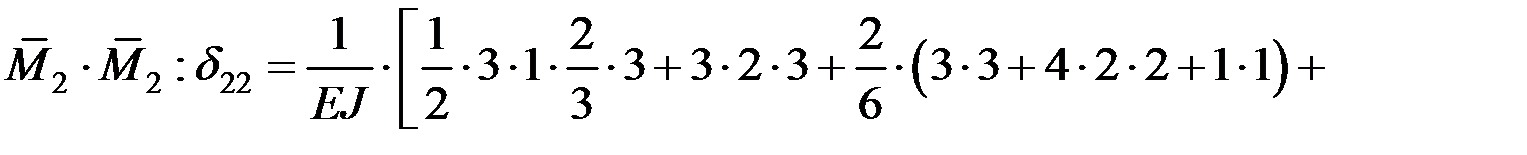
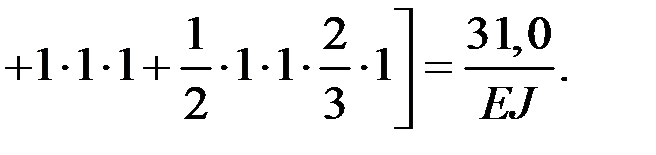
Проверка: строим суммарную единичную эпюру  , перемножаем ее саму на себя, проверяя условие
, перемножаем ее саму на себя, проверяя условие  .
.

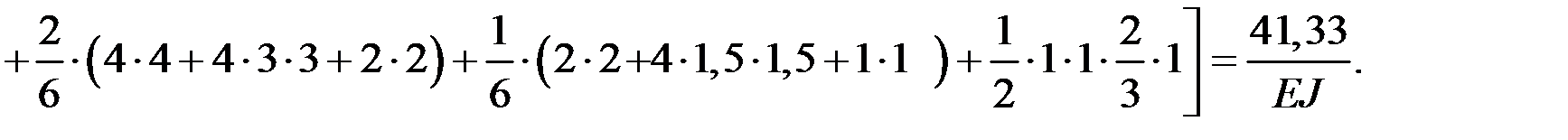
 – условие выполнено.
– условие выполнено.
4.2. Определение свободных членов системы канонических уравнений метода сил.
Для определения свободных членов 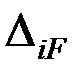 изображаем грузовое состояние основной системы и строим грузовую эпюру MF (рис. 6.7, в; 6.8, а).
изображаем грузовое состояние основной системы и строим грузовую эпюру MF (рис. 6.7, в; 6.8, а).
Для определения опорных реакций составим уравнения равновесия основной системы в ее грузовом состоянии (рис. 6.7, в):

откуда 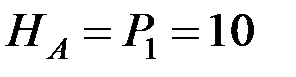 кН;
кН;
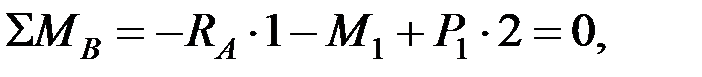
откуда  кН;
кН;

откуда 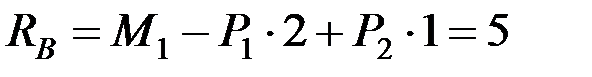 кН.
кН.
Грузовую эпюру моментов строим методом сечений по участкам (см. задачу 4). Свободные члены определяем путем перемножения единичных и грузовой эпюр по методу Мора–Верещагина (с использованием формулы Симпсона):
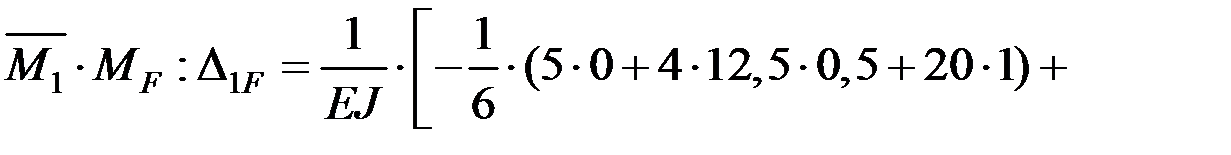
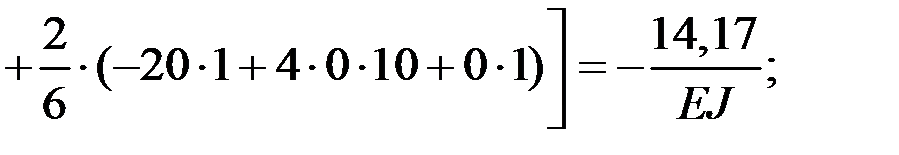
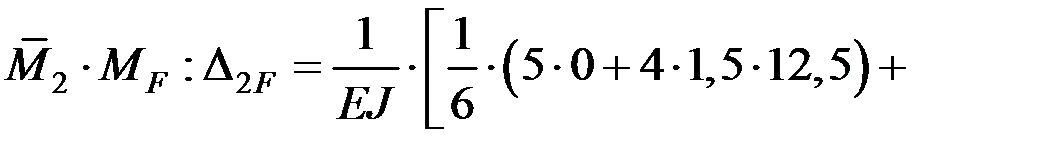
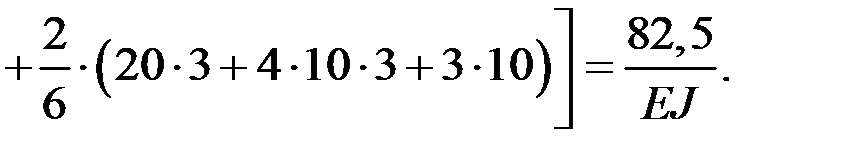
Проверка: перемножаем суммарную единичную и грузовую эпюры, проверяя условие:
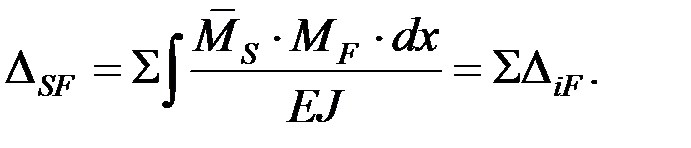
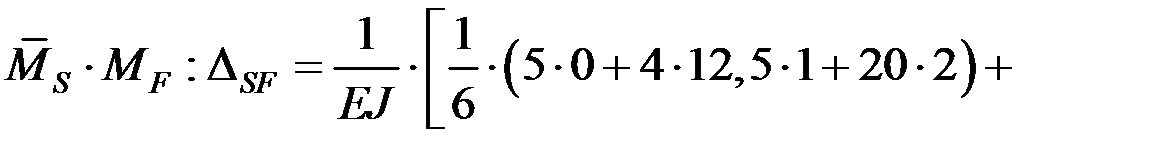
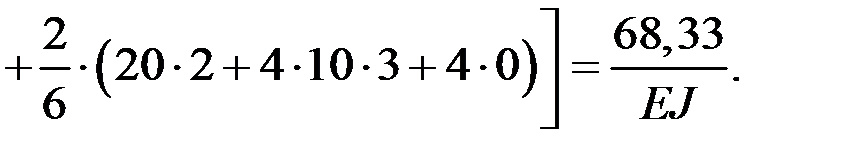
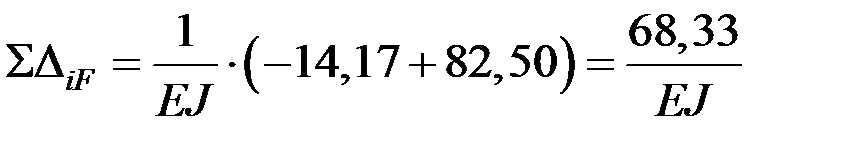 – условие выполнено.
– условие выполнено.
4.3. Решение системы канонических уравнений метода сил.
Подставляя найденные коэффициенты и свободные члены в систему канонических уравнений и сокращая на EJ, решаем систему:

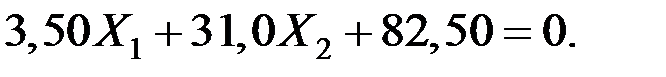
В результате решения системы получим:
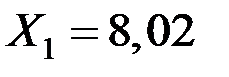 кН,
кН,
 кН.
кН.
Проверка: подставляем полученные значения в одно из уравнений системы (например, во второе):
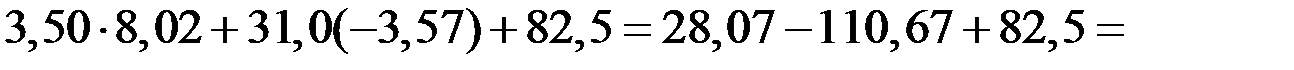
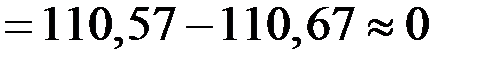 .
.
Система решена верно.
|
|
|
|
|
Дата добавления: 2015-06-30; Просмотров: 1352; Нарушение авторских прав?; Мы поможем в написании вашей работы!